up主从在高一第一次见到类似2^x=x^2根个数的问题开始,就一直恼于解答此类问题,虽然上面这题可以通过图像和代值得出答案,但不知道通法就总是过意不去(不知道有没有和我一样的人233)。那么现在我们就一口气把它解决了吧(非专业性,只求看懂)

一、变形
(1)当x=0时,左边=1≠右边=0,故0不是该方程的根
(2)当x>0时,对两边同时取对,有
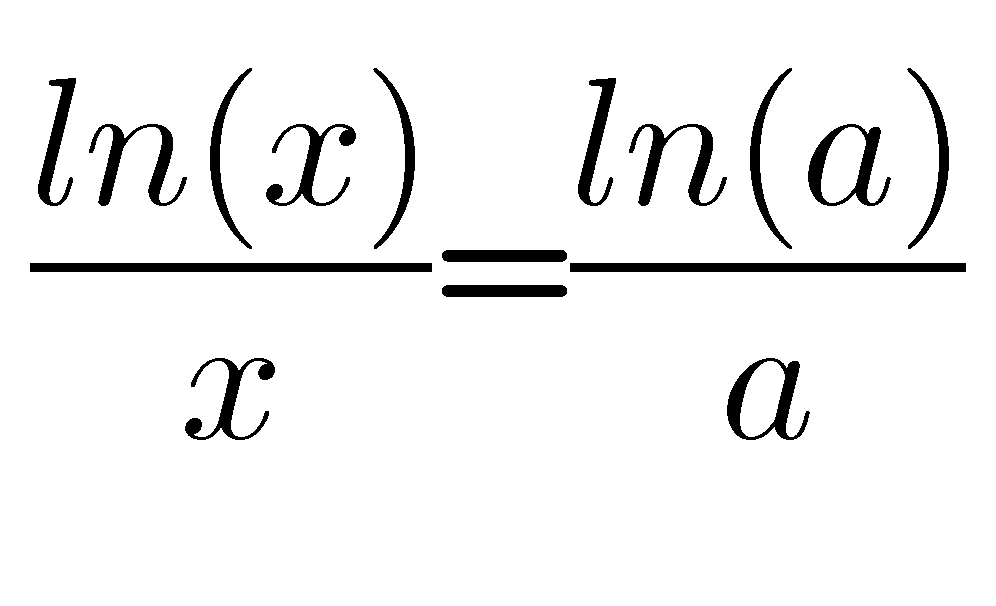
(3)当x<0时,我们就要注意一下幂函数的图像性质
①第一象限一定有图像且一定过点(1,1);第四象限一定没有图像
②若是奇函数,则第三象限有图像;若是偶函数;则第二象限有图像;若是非奇非偶函数,则只在第一象限有图像
(关于幂函数奇偶性的判断放在文章最后面)
再考虑指数函数的图像,我们可知只有y=x^a是偶函数时,x<0时该方程才有根,此时原方程化为
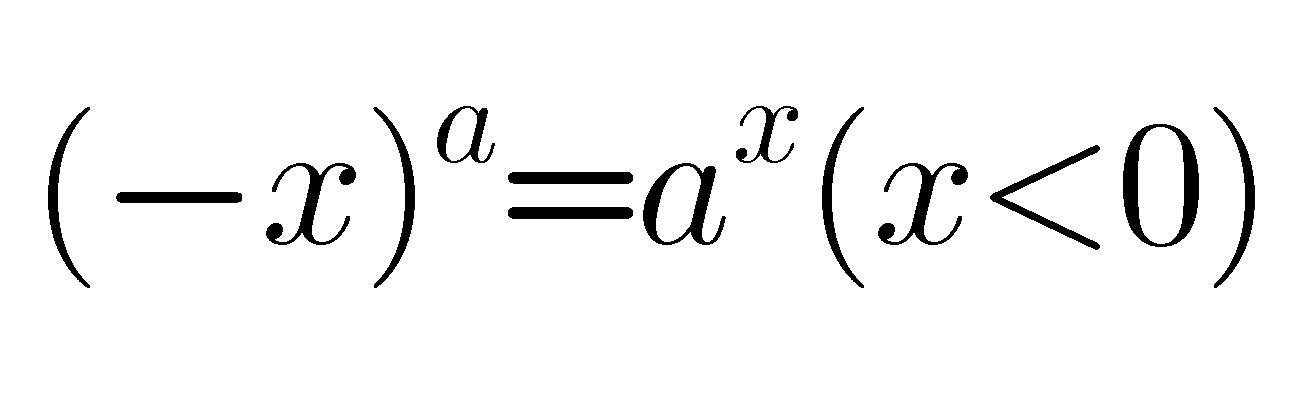
再取对,有
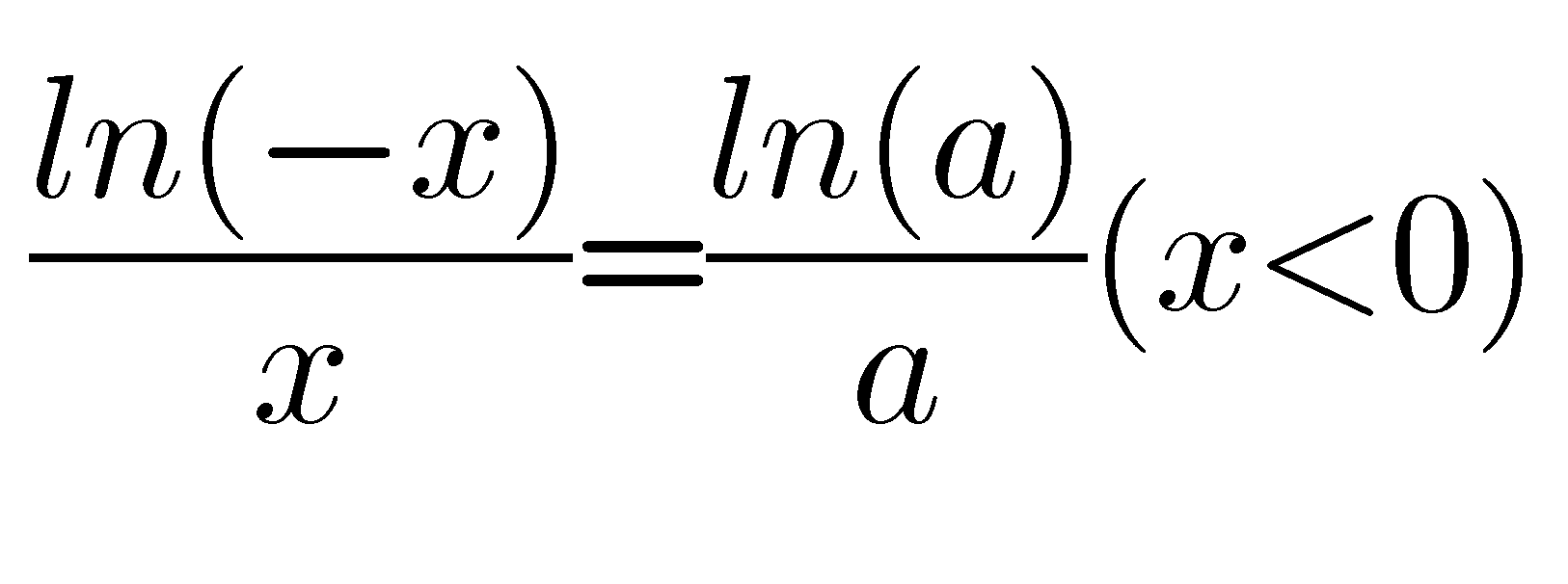
我们还注意到,上述两个方程的右边可以统一为ln|x|/x,为此,我们要讨论的就是
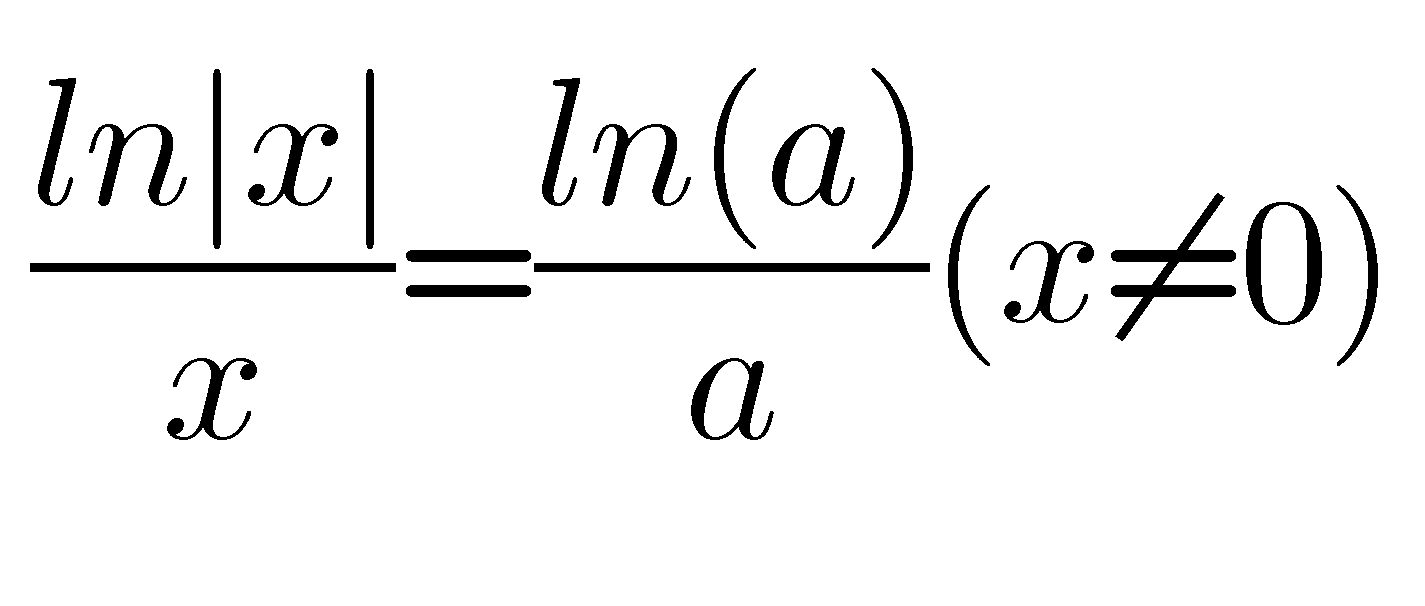
根的个数

二、作图(这一步大家应该都会我就不赘述了,看图吧)
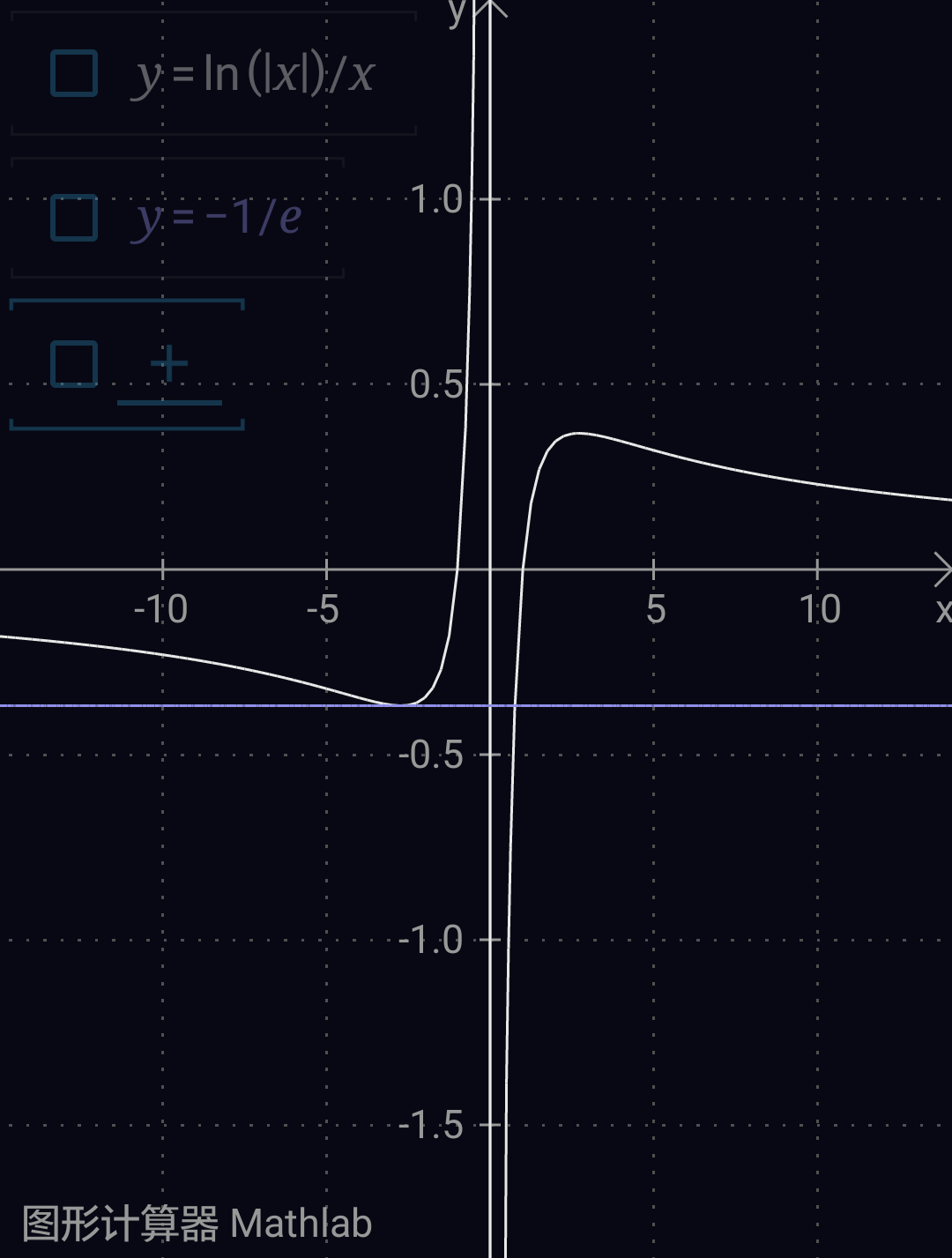
借助强大的图形计算器,我们还得到y=-1/e与右边曲线的交点横坐标是个无理数(这点很重要),且约为0.757。同时ln(a)/a的值就可以从右边曲线直接看出,因此我们得到
①0<a<0.757时,直线y=ln(a)/a只和曲线y=ln|x|/x左边无交点,和右边有一个交点,故此时方程只有一个正根,且这个根就是a
②a=0.757时,直线y=ln(a)/a和曲线y=ln|x|/x的左右两边各有一个交点,但注意,上面我们说了此时0.757只是一个近似值,它实际上是一个无理数,所以此时y=x^a其实是非奇非偶函数,故仍然只有一个正根,且这个根就是a
③0.757<x<1时,直线y=ln(a)/a和曲线y=ln|x|/x的左边有两个交点,右边有一个交点,此时一定有根a。若y=x^a还是偶函数,那么另有两负根,一根∈(-∞,-e),一根∈(-e,-1)
④x=1时,和②类似,虽然左右各有一根,但y=x是奇函数,所以只有一个正根,为1
⑤x>1且x≠e时,直线y=ln(a)/a和曲线y=ln|x|/x的左边有一个交点,右边有两个交点,此时一定有两正根,一根∈(1,e),一根∈(e,+∞),且有一个为a。若y=x^a还是偶函数,那么另有一负根∈(-1,0)【准确说是∈(-1,-0.757)】
⑥x=e时,y=x^e是非奇非偶函数,所以只有一个根e
因此,方程a^x=x^a最少有一根,最多有三根
最后,我们可以轻松求解开头的问题了,a=2符合⑤,故2^x=x^2有三个根:一个负根∈(-1,0)【准确说是∈(-1,-0.757)】,一根∈(e,+∞)【其实就是4】,还有一根为2

附录: 对于函数y=x^a(a∈R)
(1)a∈Q时
①若a∈Z,则
a为奇⇔y=x^a为奇函数;
a为偶⇔y=x^a为偶函数
②若a∉Z,设a=p/q(p、q∈Z),则
p为奇,q为奇⇔y=x^a为奇函数
p为偶,q为奇⇔y=x^a为偶函数
p为奇,q为偶⇔y=x^a为非奇非偶函数
(2)a∉Q时,y=x^a必为非奇非偶函数

好了,本人(高中生)的第一篇文章到这里就结束了,非常非常感谢看到这里的你。如果大家可以从这篇文章收获到什么,我会很开心的;如何大家对文章有疑义,也可以在评论区提出,有幸的话,我们下次再见
