 资源简介
资源简介
(共24张PPT)
人教版数学
五年级上册
人教版数学五年级(上)
练习二十三
多边形的面积
6
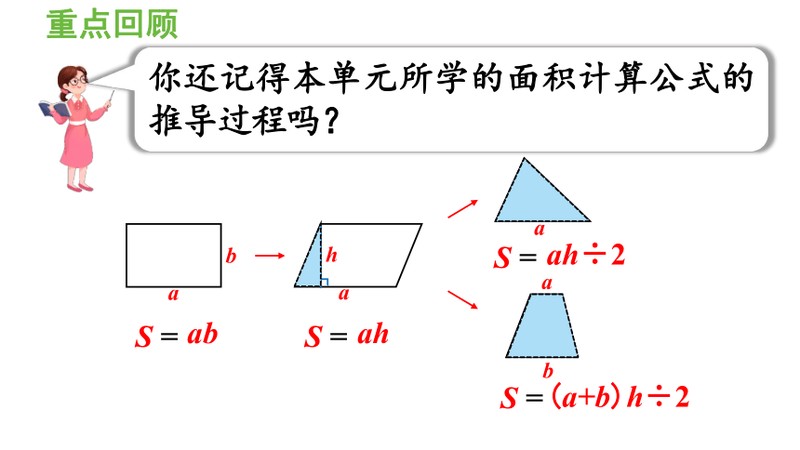
你还记得本单元所学的面积计算公式的推导过程吗?
a
b
S =
ab
a
h
S =
ah
a
h
S =
ah÷2
b
h
a
S =
(a+b)h÷2
重点回顾
怎样计算组合图形的面积?
组合图形面积的计算方法
1.根据已知条件对组合图形进行分割(添补),把组合图形转化成已学过的几个简单图形;
2.分别计算出简单图形的面积;
3.对这些简单图形的面积求和或求差。
怎样估算不规则图形的面积?
估算不规则图形面积的方法
1.数方格法
(1)通过数方格确定面积的范围;
(2)按照“不满一格的都按半格计算”的方法,数出不满一格的格数并换算成整格数;
(3)加上数出的整格数,即可估算出面积。
2.转化法:将不规则图形转化为已学过的规则图形来估算。
练习巩固
(教材第104页练习二十三)
1.计算下面每个图形的面积。
计算平行四边形、三角形面积时,注意底和高要相对应。
S=ah
=270(cm2)
=18×15
S=ah÷2
=144(cm2)
=36×8÷2
直角三角形是特殊情况,它的两条直角边就是三角形的底和高。
S=a2
=3.61(m2)
=1.9×1.9
S=ah÷2
=3.41(m2)
=2.2×3.1÷2
利用公式进行计算,先要找准相应的数值,再代入公式计算,最后还要加上单位。
S=ab
=4.5(dm2)
=2.5×1.8
S=(a+b)h÷2
=525(m2)
=(14+36)×21÷2
=50×21÷2
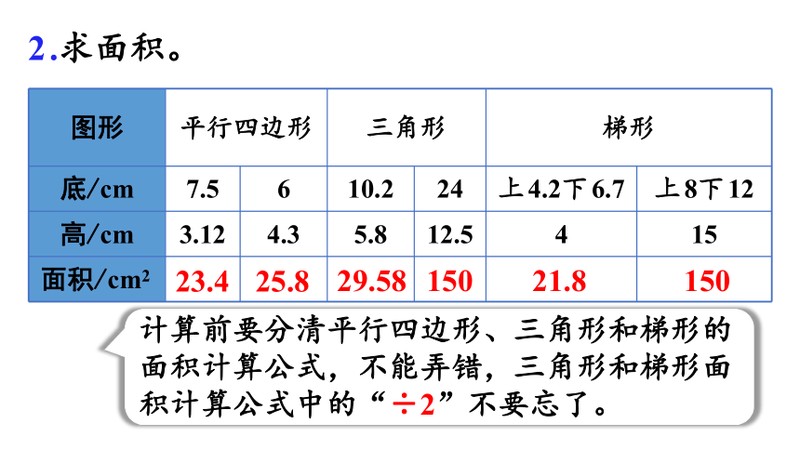
2.求面积。
图形 平行四边形 三角形 梯形 底/cm 7.5 6 10.2 24 上4.2下6.7 上8下12
高/cm 3.12 4.3 5.8 12.5 4 15
面积/cm2
23.4
25.8
29.58
150
21.8
150
计算前要分清平行四边形、三角形和梯形的面积计算公式,不能弄错,三角形和梯形面积计算公式中的“÷2”不要忘了。
3.下图是教室的一面墙。如果砌这面墙平均每平方米用砖 185 块,一共需要用多少块砖?
这面墙由一个三角形和一个长方形组成。先求面积,再求共需用砖的块数。
长方形:5×4 = 20(m2)
三角形:5×5÷2 = 3(m2)
墙:20+3 = 23(m2)
砖的块数:185×23 = 4255(块)
答:一共需要用 4255 块砖。
4.有一台收割机,作业宽度是1.8 m。每小时行5 km,大约多少小时可以收割完下边这块地?
200 m
330 m
100 m
先求这块地的面积,然后计算出收割机的工作效率,最后算工作时间。
5 km = 5000 m
1.8×5000 = 9000(m2)
(200+330)×100÷2 = 26500(m2)
26500÷9000 ≈ 3(时)
答:大约3小时可以收割完这块地。
5.先设法求出下面每个图形的面积,再比较它们的面积。你发现了什么?
先量出每个图形的底边或上底、下底的长度,然后量出它们的高,再根据面积公式计算,最后比较大小。
观察表格发现,四个图形的高相等,面积也相等。长方形的宽和平行四边形的底相等,梯形上下底的和与三角形的底都是平行四边形底的2倍。
长方形
平行四边形
梯形
三角形
量得宽1.5 cm、长2.4 cm,面积是3.6 cm 。
量得底1.5 cm、高2.4 cm,面积是3.6 cm 。
量得上底1 cm、下底2 cm、高2.4 cm,面积是3.6 cm 。
量得底3 cm、高2.4 cm,面积是3.6 cm 。
6.两艘军舰同时从相距948 km的两个港口对开。一艘军舰每小时行38 km,另一艘军舰每小时行41 km。经过几小时两艘军舰相遇?
948÷(38+41)
=12(时)
=948÷79
答:经过12小时两艘军舰相遇。
这是一道相遇问题,相遇时间=总路程÷两军舰的速度之和。
7.下面是一个火箭模型的平面图,计算它的面积。
三角形: 8×10÷2 = 40(cm )
长方形:70×8 = 560(cm )
梯形:(8+16)×8÷2 = 96(cm )
平面图:40+560+96 = 696(cm )
答:它的面积是 696 cm 。
这个平面图可分成一个三角形、一个长方形和一个梯形。
8*.图中小方格的边长是1 m,请你估计涂色部分的面积。
=26+42÷2
=47(m2)
=26+21
答:涂色部分的面积大约是47m2 。
本题可采用数方格的方法进行估计。
S=S全格+S半格
梯形:(4+8)×9÷2 = 54(m2)
涂色部分:54 - 8 = 46(m2)
长方形:4×2 = 8(m2)
答:涂色部分的面积大约是46 m2 。
也可把涂色部分看作中间挖去一个长方形的梯形。
8*.图中小方格的边长是1 m,请你估计涂色部分的面积。
9.如图是用手工纸剪的一棵小树,它的面积是多少?(单位:cm)
三角形:(0.6×2+1×2)×3÷2=4.8(cm2)
上面梯形:[1×2+(1+2.3)×2] ×3÷2=12.9(cm2)
小树:4.8+12.9+18.9+12=48.6(cm2)
下面梯形:[2.3×2+(3+1)×2] × 3÷2=18.9(cm2)
长方形:6×2=12(cm2)
答:它的面积是48.6 cm2 。
这棵小树可分成一个三角形、两个梯形和一个长方形。
1.用一张长45 cm、宽21 cm 的手工纸,能剪几棵上面第9题中的小树?(请画图展示)
依题意,要根据小树高和最宽处的数据,并结合操作实际加以确定。
5棵
6棵
拓展提升
小树高是3+3+6 = 15(cm),最宽处是3+2+3 = 8(cm)。根据实际情况排列,主要有以下5种情况:
8棵
8棵
10棵
解答本题时,不能简单地用手工纸的面积除以小树的面积,还要考虑实际操作的具体情况。
2.下图直角三角形中的空白部分是正方形,正方形的一个顶点D将这个直角三角形的斜边分成两部分(AD长3 cm),阴影部分的面积是6 cm ,则DB长多少厘米?
3 cm
如图所示:将涂色小三角形绕点D逆时针旋转90°,就可以把两个阴影部分合成一个直角三角形。
A
C
B
D
6×2÷3=4(cm)
答:DB长4 cm。
A1
(12+6+12)×5÷2=75(cm )
这样整理和复习中的第2题就有了另一种解法:转化为一个梯形。
从上面的解题中,我们发现有些组合图形通过平移、旋转等可以转化成已学过的规则图形,这样方便我们分析和解决问题。
展开更多......
收起↑
 资源预览
资源预览







 资源预览
资源预览








