050f663c0b56b5177f1f9a418febca2b.png

拉普拉斯方程

泊松方程：

现在仅仅对

的区域感兴趣，因此泊松方程约化为拉普拉斯方程：

先利用拉普拉斯方程在不同坐标系下展开的公式：

证明过程请看如下Note：

Young Quantum：拉普拉斯方程不同坐标系下的表示​zhuanlan.zhihu.com
35581d8edd0422446c004e255035f644.png

唯一性定理

第一唯一性定理：在某个区域

内的拉普拉斯方程的解由电势
在这个区域的边界面
上的值所唯一决定。

唯一性定理打开了我们的想象空间：无论用什么方法得到解毒无关紧要；只要（a）它满足拉普拉斯方程，（b）它满足边界条件，则它就是正确的解。

推论：如果（a）电荷密度遍布区域

，（b）电势在所有的边界都已指定，则区域
内的电势是唯一确定的。

第二唯一性定理：设在一个区域

中有导体存在，并且有给定的电荷密度
，如果每个导体上的总电荷已经给定，则电场是唯一确定的。（整个区域可以被另外的导体所包围，也可以不被包围。）

镜像法

典型镜像问题：假定一个点电荷

位于一个无限大接地导体板上方，与板距离为
，求解板上方的电势是什么？

从数学的观点看，我们关心的问题是在

区域求解泊松方程，在
处有一个点电荷，其边界条件为：
  1. 当
    时
    （因为导体板是接地的）；
  2. 当远离电荷时
    （远离是指
    ）

根据第一唯一性定理的推论保证了仅仅有一个函数满足上述要求，从而导致只要找到一个镜像电荷使得该系统依旧满足边界条件，那么解的函数是一致的。

其他镜像问题：此方法并不局限于单个点电荷：任何靠近接地导电面的稳定电荷分布都可以通过引入它的镜像电荷这种方法处理——因此命名为镜像法。（镜像法具有相反的符号：这保证了在接地导电面电势为零。）现在介绍一个优美的模型：

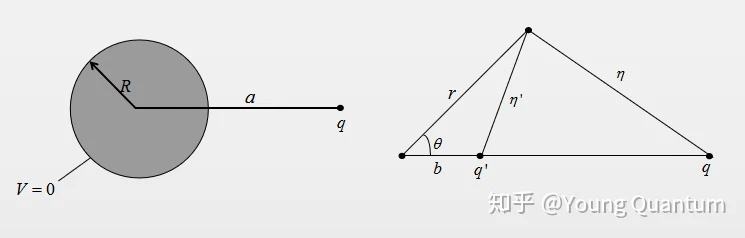
e502a5206cb23bd58d88ced3637dbcbc.png

其中根据上述技巧可以得出：

，

现在没有导体——仅两个电荷。其中可以得出这个构型的电势为：

结论：该电势方程就是一个靠近导体球点电荷的电势。（注意，

小于
，所以镜像电荷
安全地位于球内——你不能把镜像电荷放在你要计算
的区域；这将会改变
，导致你求解的泊松方程的源将是错误的。）

分离变量法

直角坐标系：

其步骤先设：

，然后带入拉普拉斯方程中将得到：
，根据独立变量线性无关可以得出：
，其中
。

然后求解各微分方程即可，最后根据边界条件求出各系数。（常常会采用傅里叶变换求解）

球坐标系：

若所给问题具有轴对称性，所以

不依赖于
；这种情况下拉普拉斯方程化为：

依旧采取同方法，设解为：

同样如此，求解微分方程。

对径向求解欧拉方程（技巧：换元

），其解为：

对

变量为勒让德方程:
，其解为（以变量
表示的勒让德多项式）：

可由罗德里格公式定义：

，

其通解是分离变量解的线性叠加：

其勒让德多项式的模方为：

上述是此模型满足轴对称性，当满足球对称性时

即不依赖
也不依赖
。

当非对称性模型时，其解将用球谐函数表示：

其简便记法可参考：

Young Quantum：勒让德多项式与球谐函数​zhuanlan.zhihu.com
a70611d351ccef3716fb2101d5c20abe.png

多极展开

远距离处的近似电势：如果你远离一个局域电荷分布，它“看起来”很像一个点电荷，它的电势—作为一个很好的近似—为

，这里
是总电荷。

现在对一种非常特殊的电荷分布情况：对任意的局域电荷分布，介绍以

幂次系统展开的方法。

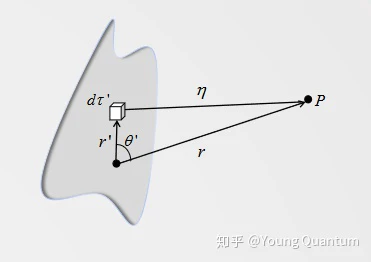
7b77a745b803d0da103adaf6a708e6ae.png

在

点的电势为：

利用远点近似以及相应的泰勒展开，可以得出公式：

，具体证明可以参考母函数：
Young Quantum：母函数的导出​zhuanlan.zhihu.com
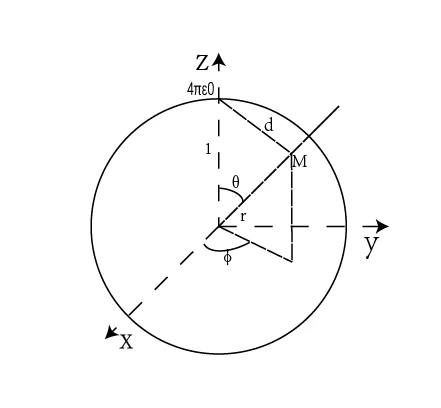
2c51afcd4e226ee6779a41fdae0d7472.png

从而得出：

展开前几项有：

这便是

按
幂次的
多极展开。

单极项和偶极项：多极展开的主要贡献来自于单极项：

，其中

，如果总电荷微零，对电势的主要贡献是偶极：

，其中

简化的表示为：

，偶极矩：
从而得出：

多极展开中坐标原点：移动原点时，单极矩

并不改变，因为总电荷显然不依赖于坐标系的。但是对偶极矩将会改变，假定将原点移动了
，新的偶极矩为：

特别有，当

，则
。（因此，在求解偶极矩的时候，如果
时，则要特别注意原点的选择。）

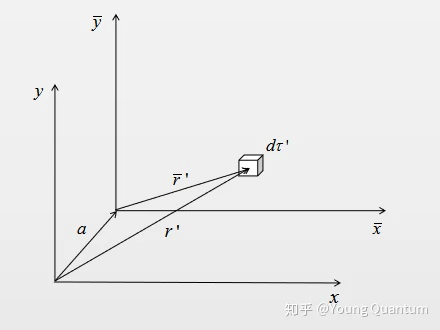
2098aa82acbf85030961951c22f09944.png

注：一个纯粹的偶极子的电场可以写为不依赖于坐标系的形式