【深度强化学习】2. 马尔科夫决策过程_马科夫决策过程-CSDN博客

【DataWhale打卡】周博磊博士-第二节马尔科夫决策过程，主要内容：

这部分主要讲的除了MDP问题本身，主要是动态规划方面的求解方法。

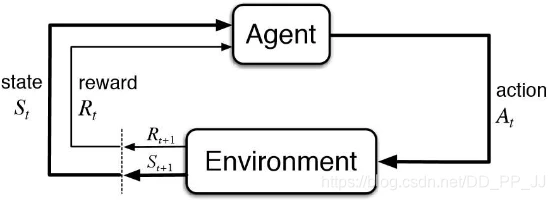
Agent 在得到环境的状态过后，它会采取行为，它会把这个采取的行为返还给环境。环境在得到 agent 的行为过后，它会进入下一个状态，把下一个状态传回 agent。

在强化学习中，这个交互过程是可以通过马尔可夫决策过程来表示的，所以马尔可夫决策过程是强化学习里面的一个基本框架。

在马尔可夫决策过程中，它的环境是 fully observable ，就是全部可以观测的。但是很多时候环境里面有些量是不可观测的，但是这个部分观测的问题也可以转换成一个 MDP 的问题。

如果一个状态转移是符合马尔可夫的，那就是说一个状态的下一个状态只取决于它当前状态，而跟它当前状态之前的状态都没有关系。
如果某一个过程满足马尔可夫性质(Markov Property)，就是说未来的转移跟过去是独立的，它只取决于现在。马尔可夫性质是所有马尔可夫过程的基础。

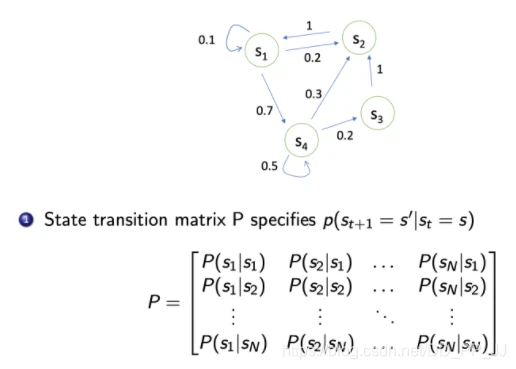
可以用状态转移矩阵(State Transition Matrix)来描述这样的状态转移。状态转移矩阵类似于一个 conditional probability，当知道当前在 s_tst 这个状态过后，到达下面所有状态的一个概念。所以它每一行其实描述了是从一个节点到达所有其它节点的概率。

马尔可夫奖励过程(Markov Reward Process, MRP) 是马尔可夫链再加上了一个奖励函数。

在 MRP 中，转移矩阵跟它的这个状态都是跟马尔可夫链一样的，多了一个奖励函数(reward function)。

奖励函数是一个期望，就是说当你到达某一个状态的时候，可以获得多大的奖励，然后这里另外定义了一个 discount factor \gammaγ 。

horizon
- 它说明了同一个 episode 或者是整个一个轨迹的长度
- 它是由有限个步数决定的。
return的定义
- Return 说的是把奖励进行折扣，然后获得的这个收益。
- Return 可以定义为奖励的逐步叠加，然后这里有一个叠加系数 $\gamma$ ，就是越往后得到的奖励，折扣得越多。
- 这说明其实更希望得到现有的奖励，未来的奖励就要把它打折扣。
state value function
- 然后对于这个MRP，它里面定义成是关于这个 return 的期望， $G_t$ 是之前定义的 discounted return。
- 这里取了一个期望，期望就是说从这个状态开始，你有可能获得多大的价值。
- 所以这个期望也可以看成是一个对未来可能获得奖励的它的当前价值的一个表现。就是当你进入某一个状态过后，你现在就有多大的价值。

这里解释一下为什么需要 discount factor。

有些马尔可夫过程是带环的，它并没有终结，想避免这个无穷的奖励。
并没有建立一个完美的模拟环境的模型，也就是说，对未来的评估不一定是准确的，不一定完全信任的模型，因为这种不确定性，所以对未来的预估增加一个折扣。想把这个不确定性表示出来，希望尽可能快地得到奖励，而不是在未来某一个点得到奖励。
如果这个奖励是有实际价值的，可能是更希望立刻就得到奖励，而不是后面再得到奖励（现在的钱比以后的钱更有价值）。
在人的行为里面来说的话，大家也是想得到即时奖励。
有些时候可以把这个系数设为 0，设为 0 过后，就只关注了它当前的奖励。也可以把它设为 1，设为 1 的话就是对未来并没有折扣，未来获得的奖励跟当前获得的奖励是一样的。

蒙特卡罗采样法：比如计算 $V(s_4)$ 的值，那么就采样从s4开始很多轨迹，到最终的价值，平均一下作为value值。

贝尔曼等式：Bellman Equation 定义了当前状态跟未来状态之间的这个关系。

s′ 可以看成未来的所有状态。
转移 P(s’|s) 是指从当前状态转移到未来状态的概率。
第二部分可以看成是一个 Discounted sum of future reward。
V(s’) 代表的是未来某一个状态的价值。从当前这个位置开始，有一定的概率去到未来的所有状态，所以要把这个概率也写上去，这个转移矩阵也写上去，然后就得到了未来状态，然后再乘以一个 $\gamma$ ，这样就可以把未来的奖励打折扣。

未来打了折扣的奖励加上当前立刻可以得到的奖励，就组成了这个 Bellman Equation。Bellman Equation 的推导过程如下：

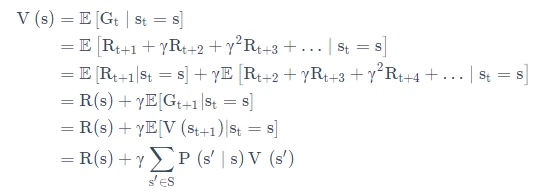
Bellman Equation 就是当前状态与未来状态的迭代关系，表示当前状态的值函数可以通过下个状态的值函数来计算。

Bellman Equation 因其提出者、动态规划创始人 Richard Bellman 而得名，也叫作“动态规划方程”。

可以把 Bellman Equation 写成一种矩阵的形式。首先有这个转移矩阵。当前这个状态是一个向量 $[V(s_1),V(s_2),\cdots,V(s_N)]^T$