一、几何证明法:对应于欧几里德的辗转相除法求最大公因子。
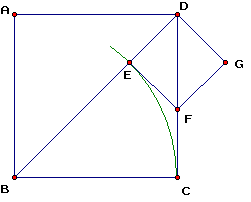
此方法是找BD和BC的公度量,BC为单位长(有理数长度,可公度),如果能找到,则BD长是有理数(可公度),否则是无理数(不可公度)。
求公度量的方法是:不断地用较长的那个线段减短的线段,直到两者相等。
如上图所示:1、用BD-BC=DE=CF;2、BC-CF=BC-DE=DF;3、DF-DE回到第一步,所以永无止境,故找不到共度量,得证。
二、数学反证法:
设sqrt(2)=p/q,则p^2=2*q^2,设p与q互质(不互质的话可约去公因子直到二者互质);所以p是偶数,设p=2*r,则4*r^2=2*q^2,所以q是偶数,与假设矛盾,故得证。
其他巧妙的比较现代的证法可参考:http://www.tzhledu.net/blog/user1/8355/20101129141616.html
