一、非齐次线性方程组,无解,多解,唯一解
非齐次线性方程组,就是方程组的等式右边不为0的方程组,系数加上方程等式右边的矩阵,叫做增广矩阵。
【例1】求解下列线性方程组
化简后的有效方程组个数小于未知数个数,有多个解。

第一步,先列出增广矩阵:
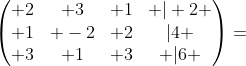
第二步,用高斯消元法化简,化简成阶梯矩阵
先把第2行换到第1行
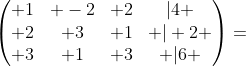
第2行减第1行的2倍,第3行减第1行的3倍,得到
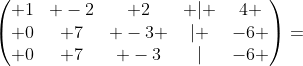
第3行减第2行,得到
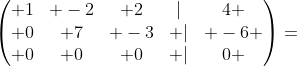
化简后的方程组,等于

这样,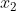 可以通过
可以通过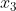 来表示,
来表示,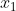 也可以通过
也可以通过 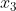 来表示,这样
来表示,这样 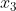 就叫做自由变量,
就叫做自由变量,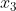 可以取任意值。所以
可以取任意值。所以 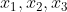 就有无穷多个解。
就有无穷多个解。
可见,化简后的有效方程组个数,小于未知数个数。
有效方程组个数=2,未知数个数=3
化简后的有效方程组个数,小于未知数个数。这样的方程组有无穷多个解化。即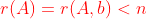 。
。
【例2】求解下列线性方程组
化简后的有效方程组出现(0=d)型式不兼容方程,则无解化。

第一步,先列出增广矩阵:
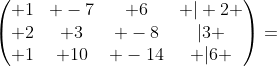
第二步,用高斯消元法化简,化简成阶梯矩阵。
第2行减去第1行*2,第3行减去第2行
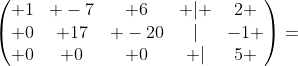
导出最后一个方程:
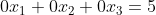
这个方程是不可能成立的,所以原线性方程组无解。
这种形式的方程叫做 {0=d} 方程,其中d是非零数,这种叫做不相容方程,也是自相矛盾的方程。
{0=d} 方程是一种自相矛盾的方程,左边全是0,右边是一个非零,这是自相矛盾的,是不相容的,所以无解。
化简后导出 {0=d} 形式的方程,方程组无解。
判断有解无解总结:
对于 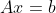 方程组
方程组
通过高斯消元法,化简,化成阶梯行方程组
- 先看看是否出现{0=d}形式的不相容方程,如果出现,无解。
- 有解的情况下,再看看有效方程个数是否小于未知数个数,如果是,则有无穷多个解。如果正好相等,则有唯一解。
二、齐次线性方程组,非零解,零解
齐次线性方程组,就是方程组的等式右边全部是0的方程组,只有系数矩阵,不需要增广矩阵,所以不会出现{0=d}形式的不相容方程。所以不会出现无解的情况,只需要考虑是多个解,还是唯一解。
对于齐次线性方程组,有多个解叫做有非零解。唯一解叫做零解。多个解叫做有非零解。唯一解叫做零解。
对于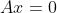 的齐次线性方程组,列出其系数矩阵(不需要增广矩阵),使用高斯消元法化简,化为阶梯形矩阵,化简后,判断有效方程组个数是否小于未知数个数。
的齐次线性方程组,列出其系数矩阵(不需要增广矩阵),使用高斯消元法化简,化为阶梯形矩阵,化简后,判断有效方程组个数是否小于未知数个数。
如果有效方程组个数小于未知数个数,叫做有非零解(多个解) 。如果等于,叫做只有零解(唯一解)。
三、什么是矩阵的秩(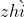 ),什么是detA?
),什么是detA?
detA就是矩阵A的行列式的值。
什么叫做矩阵的秩?
将矩阵用高斯消元法化简后,非零行的行数叫做行秩,非零列的列数叫做列秩。
矩阵的秩是方阵经过初等变换后的非零行行数或非零列列数。
可以将矩阵看成一个个行向量或者列向量,秩就是极大无关组中所含向量的个数。
定义: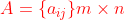 的不为零的子式的最大阶数称为矩阵A的秩。
的不为零的子式的最大阶数称为矩阵A的秩。
记做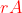 ,或者
,或者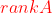 。
。
特别规定零矩阵的秩就是零。
若A中至少有一个r阶子式不等于零,且在r< min(m,n)时,A中所有的r+1阶子式全为零,则A的秩为r。
由定义直接可得n阶可逆矩阵的秩为n。
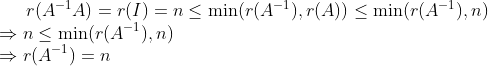
满秩矩阵才可逆(以下记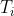 为第i个矩阵的初等变化):
为第i个矩阵的初等变化):
如果矩阵A是满秩的,我们就可以通过一系列的初等变化将矩阵A变换为单位矩阵。
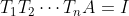
则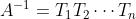
所有通常又将可逆矩阵称为满秩矩阵,满秩矩阵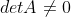 。
。
不满秩矩阵就是奇异矩阵,奇异矩阵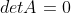
由行列式性质知道,矩阵A的转置AT的秩与A的秩是一样的。
四、通过矩阵的秩(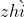 )来判断线性方程组无解,有多个解,唯一解的问题
)来判断线性方程组无解,有多个解,唯一解的问题
线性方程组什么时候无解,有多个解,唯一解?
1.对于非齐次线性方程组,用矩阵的秩r(A)来判断
对线性方程组进行初等变换(高斯消元法),化为最简型(阶梯形)矩阵。
考查系数矩阵r(A),增广矩阵r(A,b),以及方程组未知数个数n。
如果系数矩阵的秩r(A)小于增广矩阵的秩r(A,b),r(A)<r(A,b),那么方程组无解;
如果系统矩阵的秩小于方程组未知数个数,r(A)=r(A,b)<n,那么方程组有多个解。
如果系统矩阵的秩等于方程组未知数个数,r(A)=r(A,b)=n,那么方程组有唯一解。
2.对于齐次线性方程组,用行列式的值 detA来判断。
不存在无解的情况。至少有全0的解。
判断detA,如果detA=0,则有非零解(无穷多个解)。
判断detA,如果detA≠0,则只有零解(只有唯一解)。
总结
无论是对于齐次线性方程组还是非齐次线性方程组,都可以通过矩阵的秩来做判断。
只要矩阵为满秩的,则必然只有唯一解
- 对于齐次线性方程组来说唯一解为0解
- 而非齐次线性方程组的唯一解就不一定了
如果矩阵不是满秩的
- 对于齐次线性方程组而言,则有无穷多解,故存在非零解。
- 对于非齐次线性方程组而言,有两种情况:
- 一种为系数矩阵的秩与增广矩阵的秩相同,则有无穷多解。
- 如果系数矩阵的秩小于增广矩阵的秩,则无解。
参考文章
线性方程组什么时候无解?多个解?唯一解?
