这个帖子将解决一种悖论。当特征方程有双根时，解差分或微分方程的过程是不同的。但从直觉上看，有双根和有两个非常接近的根之间应该没有什么区别。

我先说说双根对寻找差分方程和微分方程的解有什么影响，然后我将重点讨论微分方程，看看双根和两根相近之间的区别。

双重根

上一篇文章看了一个二阶差分方程和一个二阶微分方程。两者都是通过类似的技术来解决的。解决差分方程的第一个步骤是

ay**n+byn-1 +cyn-2 = 0

或微分方程

ay″ +by′ +cy= 0

的第一步是找到特征方程的根

aλ² +bλ +c= 0。

如果特征方程有两个不同的根，那么每个根都会产生一个独立的差分或微分方程的解。根可能是复杂的，这改变了解决方案的定性行为，但并不改变解决的过程。

但如果特征方程有一个双根λ呢？用同样的方法可以找到一个解：λn为差分方程，exp(λt)为微分方程。根据一般定理，我们知道第二个独立的解一定存在，但我们如何找到它呢？

对于微分方程，第二个解是nλn而对于微分方程来说，t的exp(λt)就是我们的第二解。

接近的根

在文章的其余部分，我将重点讨论微分方程，尽管类似的言论也适用于差分方程。

如果λ=5是我们的微分方程的双根，那么一般解是

α exp(5t) + βtexp(5t)

但如果我们的根是λ=4.999和λ=5.001，那么一般解是

α exp(4.999t) + β exp(5.001t)

当然，这两个解不可能有那么大的差别。如果微分方程的参数是根据经验确定的，我们甚至可以分辨出双根和一对相距一线的不同根之间的区别吗？

另一方面，β exp(5t)和βtexp(5t)在大t下有很大差别。然而，这就碰上了希腊字母悖论：假设两个方程中具有相同名称的参数意味着同样的事情。当我们将相同的初始条件应用于上述两个解决方案时，我们会得到不同的α和β值，所以比较exp（5t）和texp（5t）是错误的比较。正确的比较是在两个初值问题的解之间。

我们将看两个例子，一个是λ为正，一个是λ为负。

λ>0的例子

如果λ>0，那么随着t的增加，解以指数形式增长。无论β有多小，βtexp(λt)的大小最终都是重要的。然而，微分方程中的任何误差，如初始条件的测量误差或数值计算解的误差，也将以指数形式增长。一个双根和两个附近的根之间的差异可能比初始条件的准确性更重要。

让我们看一下

y″ - 10y′ + 25y= 0

和

y″ - 10y′ + 24.9999y= 0

两者的初始条件都是y（0）=3和y′（0）=4。

前者的特征方程有一个双根λ=5，后者的特征方程有根4.99和5.01。

第一个初值问题的解是

3 exp(5t) - 11texp(5t)

而第二个初值问题的解是

551.5 exp(4.99t) - 548.5 exp(5.01t)。

注意，系数非常不同，说明了希腊字母悖论。

两个解决方案的表达式看起来是不同的，但是对于小的t，比如说小于1，它们是无法区分的。但是当t变大时，解决方案就会发散。如果我们把第一个方程解了两次，y(0)=3和y(0)=3.01，情况也会一样。

λ<0的例子

现在我们来看看

y″ + 10y′ + 25y= 0

和

y″ + 10y′ + 24.9999y= 0

两者的初始条件都是y（0）=3和y′（0）=4。注意速度系数的符号从-10变为10。

现在第一个微分方程的特征方程在-5处有一个双根，第二个方程有根-4.99和-5.01。

第一个初值问题的解决方案是

3 exp(-5t) + 19texp(-5t)

而第二个初值问题的解是

951.5 exp(-4.99t) - 948.5 exp(5.01t)。

同样，这两个解的书面形式看起来很不一样，但它们的图是无法区分的。

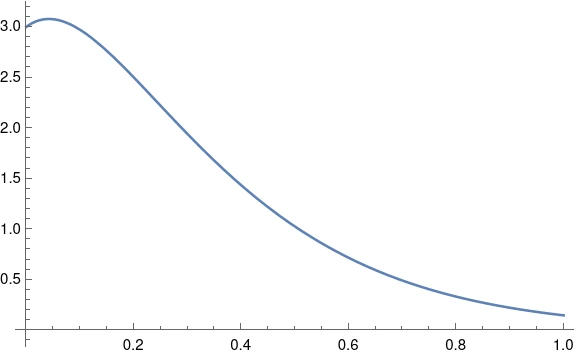
与λ>0的情况不同，现在λ<0时，两个解决方案之间的差异是有界限的。以前，这两个解开始时很接近，最后会出现分歧。现在，这些解永远都在一起了。

这是两个解决方案之间的差异图。

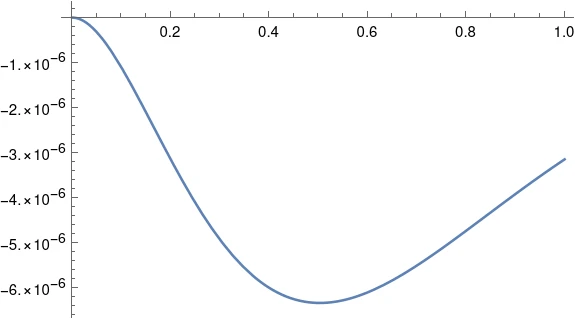
因此，两个解决方案之间的最大分离发生在t=0.5附近，在那里，两个解决方案在小数点后第六位有差异。

结论

特征方程是有双根还是有两个接近的根，对微分方程的解的书面形式有很大的影响。如果根是正的，解最初是接近的，然后发散。如果根是负的，则解总是紧密相连的。