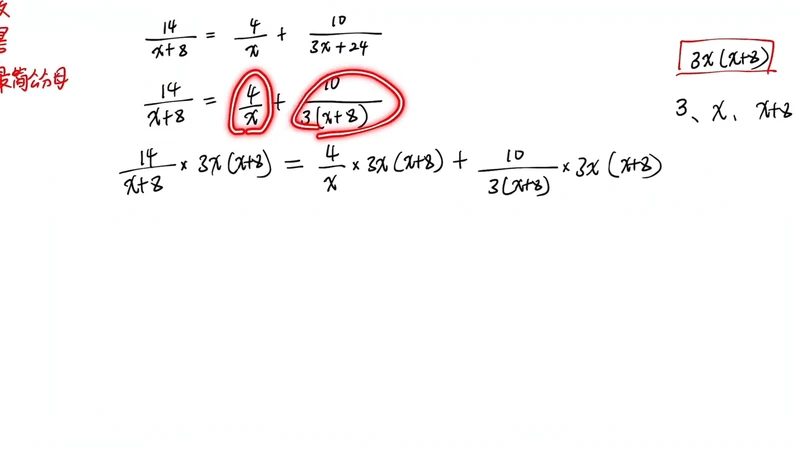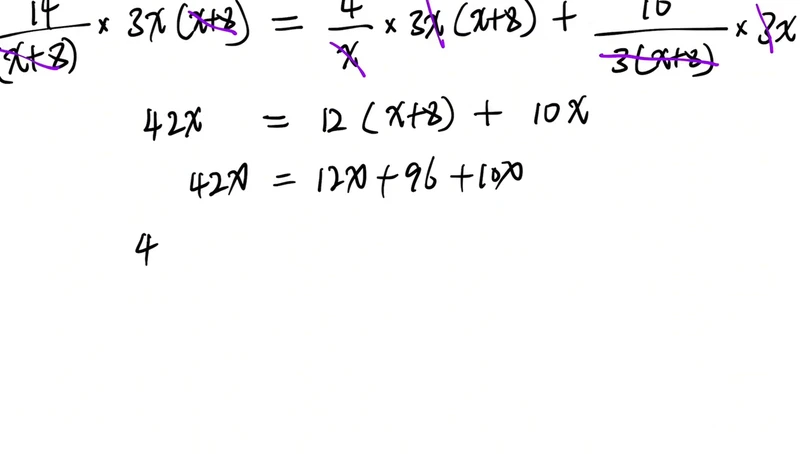说说分式方程的解法！

1. 解分式方程一共有五个步骤，每个步骤还有细分的。比如第一个步骤找最简公分母，具体如下：

- 先将所有的分母因式分解，分解完以后，分数、字母、英式找最小公倍数，字母、英式找最高次幂，把它们相乘就得到了一个最简公分母。

- 找到最简公分母以后，方程两边同时乘以最简公分母，就会把分母去掉，得到一个整式方程。求整式方程，整式方程会求出一个 x 的值，就叫做整式方程的解。将这个解带入到最简公分母里面。

- 如果最简公分母不是零，分式方程有意义，整式方程的解就是分式方程的根。如果最简公分母是零，分式方程就没有意义，整式方程的解叫做分式方程的增根，分式方程是没有意义的。

2. 来看一道题，第一步先不找最简公分母，先将所有的分母因式分解。第一个分母 x 等于 x 加 8，不需要因式分解。第二个也不需要。第三个 3x 加 24，需要因式分解，把 3x 加 24 拆成提个公因式提个 3，剩于 x 加 8。也就是说分式方程等于 x 加 8 分之 14，x 分之 4 加上，这是第三个分式的分母，分子不变，把它拆成分式方程。拆完之后，现在是把所有的分式分母因式分解。

3. 然后找数字因式，数字因式就是 3 和 1 和 1，13 的最小公倍数是 3。

4. 接着找字母因式的最高次幂，字母因式有一个 x 加 8，x 加 8 这是一样的，还有一个 x，所以字母因式的最高次幂就是 x，还有一个 x 加 8。

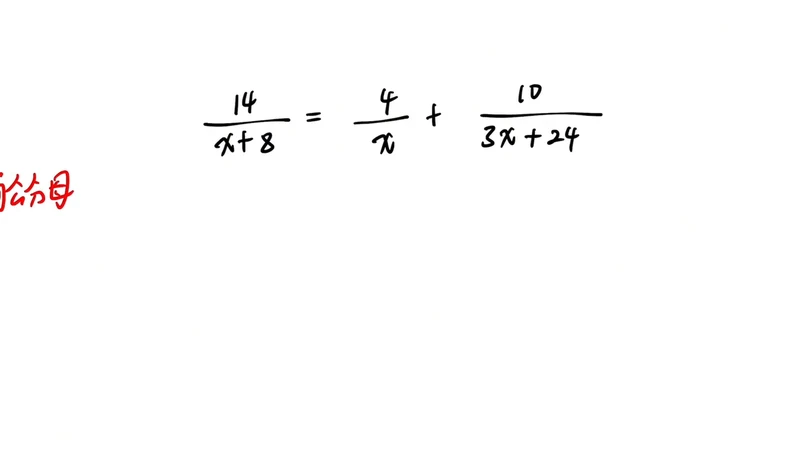
5. 把它们都相乘，就得到了一个最简公分母。也就是分式方程的最简公分母是三倍的 x 加 8，把它们乘到一块就是最简公分母，这个叫分式方程的最简公分母。

6. 方程两边同时乘以最简公分母，左边是 x 加 8 分之 14 乘以 3x 写成 3 倍的 x 加 8，右边等于它乘以最简分母。直接拆括号是每一项都要乘 x 分之 4 乘以 3x 倍的 x 加 8，还要加上三倍的 x 加 8 分之 10 乘以 3x 倍的 x 加 8。

7. 把这个稍微往外挪一挪，放这儿，长完之后是这个位置，它乘以最简公分母也要乘，变成分式乘法的化简。这是一个整体，它俩可以直接约分，换一个颜色，它俩可以直接约分掉。也就说这一步相当于区分母 x 和 x 约掉了，三倍的 x 加 8 和三倍的 x 加 8 约掉了，这一步的结果就是约分的结果化简结果。

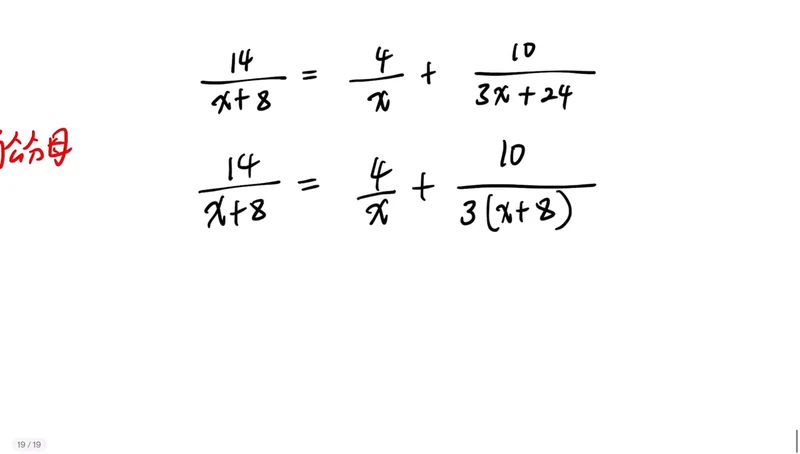
8. 4 乘以 3x 也就是 42x 等于 4 乘 3 乘 x 加 8 是 12 倍的 x 加 8 加上这个是 10，还有个 x，比方说这还有个 x 加上 10x，也就是方程两边同时乘以最简公分母会得到一个整式方程。这里乘完化简以后得到一个整式方程，整式方程求解。

9. 也就是把整式方程算出来，42x 等于去括号，12x 加上 96 加上 10x，一项 42x 减去 12x 减去 10x 等于 96，42 减 12 是 30 减 10 是 20x 等于 96，x 等于 96 除以 20，也就是五分之二十四或者是 4.8 都可以。

10. 五分之二十四或者 4.8 是整式方程的结，不一定是分式方程的根，怎么办？验证一下，刚刚算出最简公分母是不等于零，当 x 等于 4.8 时，3x 倍的 x 加 8 是不是不等于零，不等于零，也就是分式方程肯定是有意义的，最简公分母不是零，所有的分母都不是零，x 等于 4.8 就是分式方程的根，就不是增根，所以得写上。经检验 x 等于 4.8 是分式方程的根，算一下最简公分母是不是零，不是零就是根，如果这个位置正好等于零，x 等于 4.8 是分式方程的增根。看一下整个题的解题过程，画红线的部分可以不写，在草纸上算出来，比如这个步骤，这个步骤，这个步骤其实是可以不写的，但是初学者一定要写全，这是解题过程，这是解图的解题思路，同学们可以截图看一下。