贝塞尔函数
贝塞尔函数是下列常微分方程的标准解函数,这个方程是在柱坐标或球坐标系下使用分离变量法求解拉普拉斯方程和赫姆霍兹方程得到的。
贝塞尔函数的具体形式随着上述的实数
第一类贝塞尔函数
第一类贝塞尔函数
若
第二类贝塞尔函数
汉克尔函数
汉克尔函数也是贝塞尔方程的一对线性无关的解
贝塞尔函数的仿真
matlab中可以直接使用函数
besselj(n, x)
bessely(n, x)来生成第一类和第二类贝塞尔函数。
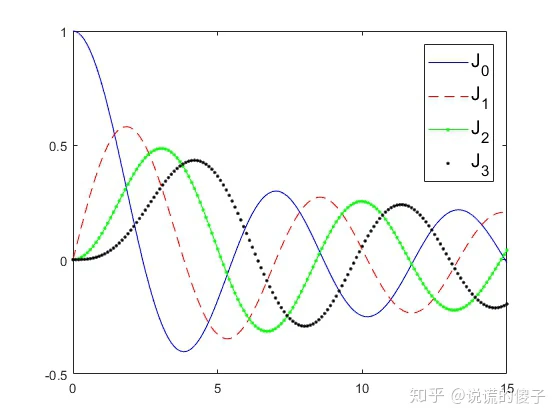
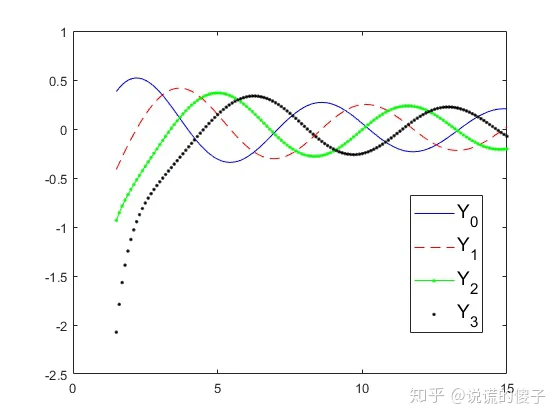
贝塞尔函数的递推关系
容易得到:
由上面两式可以得到:
对应的,可以得到:
勒让德函数
勒让德函数是勒让德方程的解:
其中
这里需要考虑
连带勒让德函数
连带勒让德函数是连带勒让德方程的解:
勒让德函数的正交性
勒让德函数的仿真
matlab里面有直接计算连带勒让德函数的函数
legendre(n, x)其中
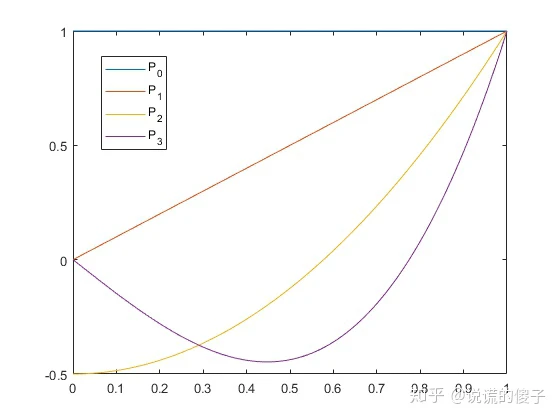
勒让德函数的递推公式
特别地,有:
