目录
〇,约定
约定:p表示素数,其他字母默认表示正整数
(a,b)表示a和b的最大公约数,即gcd(a,b)
一,数论基础
1,生成元



二,数论常用知识
1,欧拉φ函数
(1)对正整数n,欧拉函数是小于或等于n的正整数中与n互质的数的数目。
 (其中p1, p2……pn为x的所有质因数)
(其中p1, p2……pn为x的所有质因数)
(2)若(a,b)=1,则 ,即这是积性函数
,即这是积性函数
(3)1,2,3......n中,与n互素的所有数之和为
(4)由于 是积性函数,所以可以推出
是积性函数,所以可以推出
(5)如果函数f满足,任意n, ,那么f就是欧拉φ函数
,那么f就是欧拉φ函数
2,欧拉定理

PS:


3,费马小定理
若 ,则
,则
4,欧拉费马定理

5,威尔逊定理

PS:欧拉定理、费马小定理、欧拉费马定理、威尔逊定理 统称数论四大定理。
PS:出于实用性的考虑,补充一个丑陋的式子:
,其中x大于等于m的所有素因子次数中的最高次数。
6,gcd、lcm、裴蜀定理
(a,b)是最大公约数,[a,b]是最小公倍数,(a,b)[a,b] = ab
裴蜀定理: 裴蜀定理
7,唯一分解定理
(1)每个整数都有唯一的一种素因子分解形式
(2)n的正约数的个数是
(3)n的所有正约数的和是

(4)
8,取整函数
向下取整  , 也叫高斯函数
, 也叫高斯函数
向上取整 
取小数部分 
PS: 也可以写作 [x]
也可以写作 [x]
9,阶乘的性质
(1)
(2)n!中素因子p的次数d,指的是满足p^d || n!的d
利用富比尼原理得到, ![d=[\frac{n}{p}]+[\frac{n}{p^2}]+[\frac{n}{p^3}]+......](http://news.iaiso.net/uploads/202410/01/e8c1be70d4113341.webp)
(3)
![\therefore f(n,p)=[\frac{n}{p}]+f([\frac{n}{p}],p)](http://news.iaiso.net/uploads/202410/01/ff0f33b548404f59.webp) 这里的f的含义同d
这里的f的含义同d
(4)n!的十进制表示中,末尾0的个数是f(n,5)
(5)(p-1)f(n,p)=n-s(n,p),其中s是n的p进制表示法中各位数之和。
10,斯特林公式
11,费马数、梅森数、完全数
(1)若2^m+1是奇素数,则m=2^n,形如 的素数称为费马数,所有费马数之间都是互素的
的素数称为费马数,所有费马数之间都是互素的
(2)若a^m-1是奇素数,则a=2且m是素数p,形如 的素数称为梅森数
的素数称为梅森数
(3)如果 是素数,则
是素数,则 是完全数。如果n是偶完全数,则n=
是完全数。如果n是偶完全数,则n= ,其中
,其中 是梅森数
是梅森数
12,勾股数
不定方程_nameofcsdn的博客-CSDN博客
13,数论组合
(1) ,则n!中p的次数为
,则n!中p的次数为![[\frac np]+[\frac n{p^2}]+[\frac n{p^3}]+...=\frac{n-s}{p-1}](http://news.iaiso.net/uploads/202410/01/0f4a98d05ee2fa6c.webp) ,其中
,其中 是n的各位数字之和。
是n的各位数字之和。
(2)
(3)
(4)](http://news.iaiso.net/uploads/202410/01/7b8922c1cc5bf3c8.webp)
14,卢卡斯定理

其中 0<= q,r <p
15,高斯定理
n为平方和等价于n的任一4k+3型素因子的幂次为偶数
https://blog.csdn.net/nameofcsdn/article/details/79459432
16,逆元
若(a,m)=1,则 ,所以a的逆元是
,所以a的逆元是
若(a,m)不为1,则没有逆元
17,和式

其中-1次方表示逆元
18,切比雪夫定理
对于任意实数 ,一定存在素数p,使得
,一定存在素数p,使得 成立。
成立。
换句话说,所有素数从小到大排列,任意一个素数都小于前一个素数的2倍。
PS:证明在下文
19,多项式模
 则
则  有 n 个解
有 n 个解 除以 f(x)的余式的系数都是 p 的倍数。
除以 f(x)的余式的系数都是 p 的倍数。
20,二次剩余
(1)一般二次同余式 可以规约成
可以规约成 的形式
的形式
(2)如果 有解,则a叫mod m的平方剩余,否则叫非平方剩余
有解,则a叫mod m的平方剩余,否则叫非平方剩余
21,勒让德符号

22,欧拉准则
若p为奇素数,则
23,高斯引理
 对模 p 的最小非负剩余是
对模 p 的最小非负剩余是  , 若大于
, 若大于 的
的 个数为m, 则
个数为m, 则 
24,二次互反律
(1)  , 若
, 若  且 a 为奇数 , 则
且 a 为奇数 , 则 ![\left(\frac{{a}}{p}\right)=(-1)^{\sum_{k=1}^l\left[\frac{a k}{p}\right]}](http://news.iaiso.net/uploads/202410/01/5da4099388011584.webp) , 其中
, 其中 
(2) p, q 为奇质数, ![\sum_{k=1}^{u}\left[\frac{{p} k}{q}\right]+\sum_{k=1}^{l}\left[\frac{q k}{p}\right]=ul](http://news.iaiso.net/uploads/202410/01/7cfdc98ac61b8fc5.webp) , 其中
, 其中
(3) 
25,雅克比符号

其中 表示m中的所有素因子
表示m中的所有素因子
当m为素数时,雅克比符号和勒让德符号含义相同,所以用相同的符号来不矛盾。
26,合数模
(1)p为奇质数,  , 若x有解则恰有 2 解
, 若x有解则恰有 2 解
(2) ,若x有解则恰有 4 解
,若x有解则恰有 4 解
27,单质数平方和
(1)
(2)若  , 设
, 设 , 则S(k)是偶数, 且

(3)若 则
则 
 为mod p的简化剩余系
为mod p的简化剩余系
(4)若 p=4m+1, 则 
28,阶
(1)若 , 则存在 j 满足
, 则存在 j 满足 ,其中满足条件的最小j叫a模m的指数,也叫阶(Multiplicative order)
,其中满足条件的最小j叫a模m的指数,也叫阶(Multiplicative order)
In other words, the multiplicative order of a modulo n is the order of a in the multiplicative group of the units in the ring of the integers modulo n.
即以a作为单位元素的乘法同余群的阶
(2)若 x 的阶为ab,a>0,b>0,则 的阶为b
的阶为b
(3)若 x 的阶为j, 则  的阶为
的阶为 
(4)x 的阶为 a, y 的阶为 b, 如(a,b)=1,则 xy 的阶为ab
29,原根
(1)使阶为  的a 叫模m的原根f
的a 叫模m的原根f
(2)奇质数p有原根
(3)g是mod奇质数p的原根,则  ,且对于这个c,
,且对于这个c, ,进一步可证明g+pc是
,进一步可证明g+pc是 的原根
的原根
(4)奇质数p,设g是  的原根,则g与
的原根,则g与  中的奇数是
中的奇数是  的原根
的原根
(5)mod m的原根存在的充分必要条件是m=2或4或 或
或 ,其中p是奇质数
,其中p是奇质数
(6)求原根的方法:设m>1, (g,m)=1,φ(m)的所有不同质因数是
则g是mod m的原根
(7)奇质数p的原根个数是φ(p-1)
PS:(2)(7)证明在下文
30,无穷素数
(1)素数有无穷多个
(2)存在无穷多素数模4余3,存在无穷多素数模4余1
(3)狄利克雷定理:gcd(a,m)=1,则存在无穷多素数p,
(4)设不超过x的素数的个数为π(x),则 ,即x很大时,不超过x的素数个数大约就是x/lnx
,即x很大时,不超过x的素数个数大约就是x/lnx
31,素数猜想
(1)哥德巴赫猜想:大于2的偶数都可以表示成2个素数之和
陈景润证明了大于2的偶数都可以表示成一个偶数加一个2-殆素数,2-殆素数表示素数或者2个素数的乘积。
(2)孪生素数猜想:存在无穷多对孪生素数,即有无穷组素数(p1,p2)满足p2-p1=2
自从张益唐证明有无穷多组满足p2-p1<=70000000之后,这个数字在不断缩小,现在已经到246了。
(3)N^2+1猜想:有无穷多形如N^2+1的素数
目前已经证明,有无穷多形如N^2+1的数都是素数或者2个素数的乘积
32,素数测试
(1)暴力测试
枚举不超过sqrt(n)的所有素数,判断有没有n的因子
(2)费马测试
随机取1个整数a,如果 ,那么m不是素数
,那么m不是素数
多取几个a,如果 都成立,那么n有极大可能是素数
都成立,那么n有极大可能是素数
存在反例:卡米歇尔数
(3)米勒-拉宾测试(Miller–Rabin)
对于奇数n,设n-1=2^k * q,k>0,q是奇数
如果 ,且对i=0,1,2...k-1都有
,且对i=0,1,2...k-1都有
则n不是素数,反之多取几个a之后就能推断n有极大可能是素数。
事实上,如果n是合数,至少有75%的a可以用来证明n不是素数,所以只要多取几个a,准确性就非常高。
三,定理证明
1,切比雪夫定理
(1)当 时,
时,

(2)设正实数b>10, ,则
,则
设m是使得a_m>5的最大整数,则 ![(a_m,2a_m]\cup(a_{m-1},2a_{m-1}]\cup...\cup(a_1,2a_1]](http://news.iaiso.net/uploads/202410/01/2726967683135b75.webp) 覆盖(10,b],故而
覆盖(10,b],故而 
(3) 中显然没有超过2n的素数,且有如下三条定理:
中显然没有超过2n的素数,且有如下三条定理:
对于区间(1,2n]内任一素数,存在r使得,则
 中p的幂次t不超过r
中p的幂次t不超过r
对于区间![(\sqrt{2n},n]](http://news.iaiso.net/uploads/202410/01/cf1c474fb66b0cad.webp) 内任一素数p(如果存在,下同),
内任一素数p(如果存在,下同), 中p的幂次不超过1
中p的幂次不超过1
对于区间![(\frac{2n}3,n]](http://news.iaiso.net/uploads/202410/01/717eccdb6fb513af.webp) 内任一素数p,
内任一素数p, 中p的幂次为0
中p的幂次为0
故而,当n>24时有:



(4)当 时,
时, ,结合(1)(3)得,当n>500时有
,结合(1)(3)得,当n>500时有 ,即(n, 2n]内有素数。
,即(n, 2n]内有素数。
当n<=500时显然也成立,故切比雪夫定理成立。
2,奇质数有原根
对奇质数p,设 1,2,3...p-1 的阶分别为  , 令
, 令 ![{t}=lcm\left[{j}_{1}, {j}_{2} \ldots {j}_{p-1}\right]](http://news.iaiso.net/uploads/202410/01/cc3d8539265e9185.webp)
设 ,则
,则 ,
,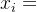 的阶是
的阶是 , 所以
, 所以  的阶是t
的阶是t
而t可以证明是等于p-1的,所以g是mod p的原根
3,奇质数p的原根个数是φ(p-1)
(1)如果n整除p-1,那么方程 恰好有n个解
恰好有n个解
(2)假设f(d)是集合{0<x<p且x mod p的阶是d}的元素个数
(3)如果n整除p-1,那么方程 的解的个数是
的解的个数是
(4) ,所以f就是欧拉φ函数
,所以f就是欧拉φ函数
(5)取n=p-1,则集合{0<x<p且x mod p的阶是p-1}的元素个数是φ(p-1),即原根个数是φ(p-1)
