今天要讲解的是这么一道题目:
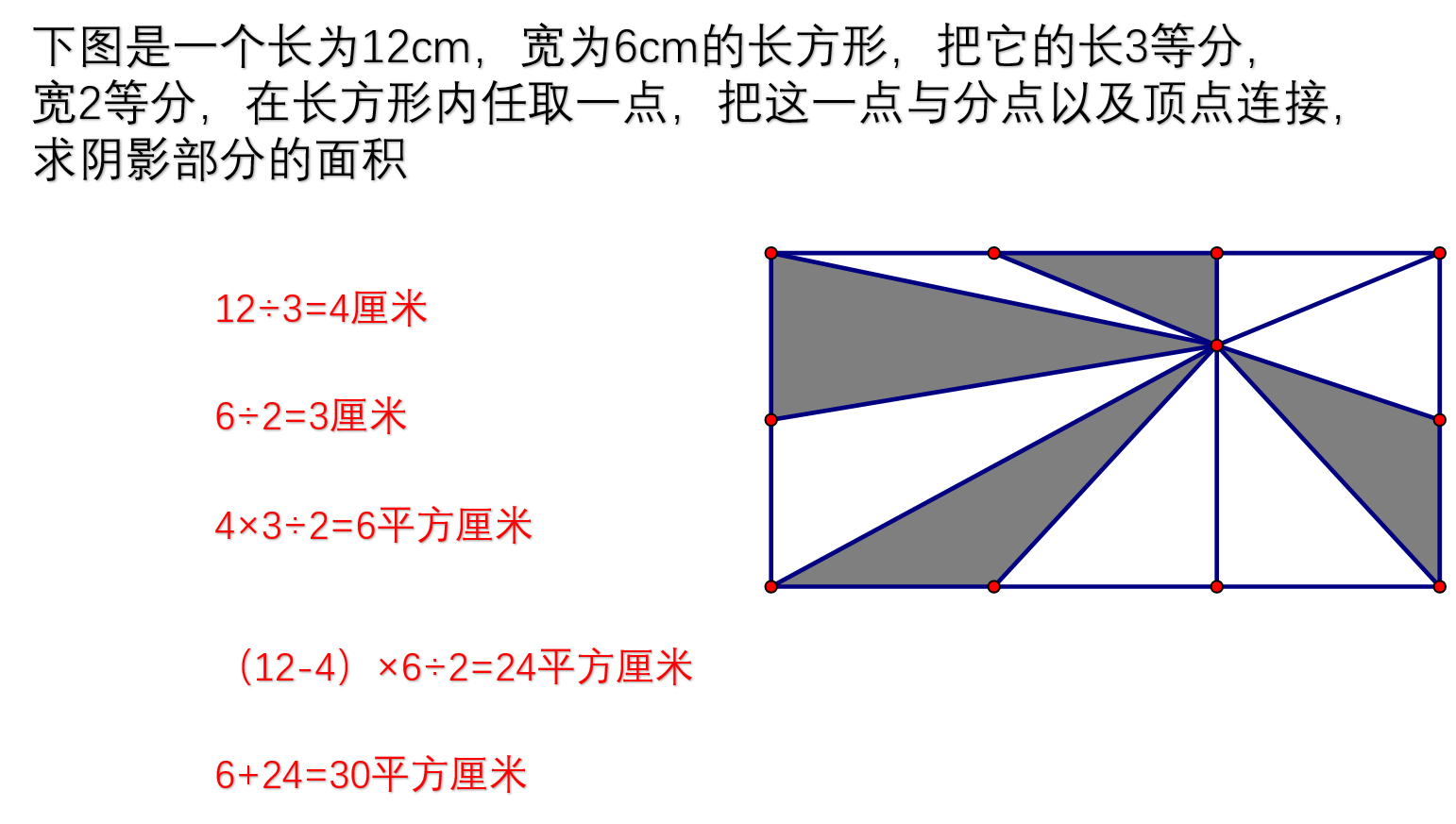
下图是一个长为12cm,宽为6cm的长方形,把它的长3等分,宽2等分,在长方形内任取一点,把这一点与分点以及顶点连接,求阴影部分的面积
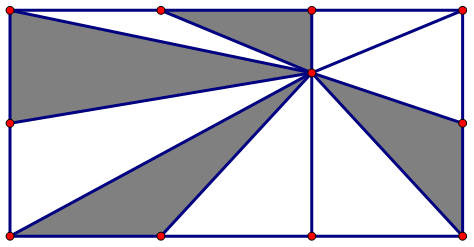
粗看这些面积,我们发现是很松散的一些,这样子不行,我们需要简单整理一下这些面积看看能发现什么。
如果分成左右两部分,我们发现,左边很密集的一片,右边只有一个三角形。
所以我们把这个图形分成左右两边
右边比较少,先计算右边,通过观察发现,右边这个三角形可以看做一个底为大长方形的宽的一半,即右边这个三角形底为6÷2=3cm,高为大长方形三等分之后的一份长度,即高为12÷3=4cm,
根据三角形面积公式:三角形的面积=底×高÷2,列出算式为3×4÷2=6平方厘米
再来看左边,左边这个长方形中可以分成3块,每块中两个三角形的面积都是相等的(以最上面的两个三角形举例,他们的底都是一样长的,都是大长方形三等分之后的一份,又公用一条高,即同高等底,因此虽然外观不同,但是面积相等。最左边的两个三角形,和下面的两个三角形亦是)
所以阴影部分面积是长方形的面积的一半
长方形面积是(12-4)×6=48平方厘米,一半就是48÷2=24平方厘米
写成综合算式就是(12-4)×6÷2=24平方厘米
所以阴影部分面积24+6=30平方厘米