事物是由数构成的,这是毕达哥拉斯派所认为的世界之本原。可能有人会疑问,为什么不称他们学派?很多人不知道的是 ,毕达哥拉斯即是一个数学学派的创始人,也是一个宗教派别的创始人。毕达哥拉斯宗派产生于人们对深沉的精神宗教的渴望,这种宗教可以提供手段来净化灵魂并保证它不朽。[1] 毕达哥拉斯学派发现在算数与几何之间有一种关系:作为点的一;一条线段上的两个端点表示二;三个点(不共线)又可以决定一个平面...... 数量和大小之间的相关性对于那些爱为宇宙中的结构和秩序寻找规则的人来说,是一个非常好的安慰。毕达哥拉斯定理就是最好的佐证[2] 在如此巨大的发现下,哲学界和科学界似乎都兴兴向荣,但是一个“异端”出现了......
芝诺悖论所带来的
当今,芝诺本人的著作早已消失在历史的长河中,我们当今熟知的(两分法悖论、阿基里斯悖论、飞矢不动、运动场悖论)则是记载在亚里士多德的《物理学》中,并被亚里士多德与后人成功解释完毕,但是芝诺悖论从根本上质疑并挑战了毕达哥拉斯学派所一直贯彻的度量和计算方式。并为后续数学的发展,打下了基础。
无理数的发现
把时针拨回现在,当代教育下,为了方便学生们的理解,便引入了“数轴”这种模型来认识数。我们最先认识到的数是自然数--N *,即0、1、2、3、4......这样数下去的0和正整数。在讲述正整数的概念时,我们又分别引出了两个和它性质各有不同的概念,即负数(第二次数系的扩充)和分数、小数(第一次数系的扩充)。我们采用在数轴上标出点的位置以表示点的大小,随着负数和分数、小数概念的引入,老师们总会问上一句:”数轴上的点越来越密, 似乎 已经将数轴填满了,真的填满了吗?“
毕达哥拉斯学派,这个曾今辉煌的学派也止步于此,毕达哥拉斯认为:
世界上只存在整数与分数,除此之外没有别的什么数了。
但就像矛和盾一样,完美无瑕的毕达哥拉斯定理的矛,终会捅破万物都是”有理数“的盾,他的门徒希帕索斯发现,当一个正方形的边长为1时,对角线的长度无法表示成一个分数的形式。这一发现,推翻了学派的理论,触动了整个学派的根基,引起了恐慌。学派封锁了该项发现,并严厉打压,但希帕索斯将自己的发现透露出去。为了躲避极刑的惩罚,他只好出逃。不幸的是,几年后他被学派忠实信徒认出,葬身赫勒斯旁海峡。
无理数
从有理数集 Q 到实数集 R
那么,有理数和无理数的差别到底在哪呢?我们不如返回到毕达哥拉斯的视角,他认为只有整数和分数是数,这已经和有理数的范围很接近了。应为那是还没有负数的概念,负数的概念要到魏晋时期的刘徽才给出准确定义。那么加上负数的这一部分,我们终于填满了有理数域。这里我们直接给出有理数(λογος,成比例的数)的定义:可以表达为两个整数比的数。
有了定义以后我们便可以开始证明为什么根号2不是有理数了。证明这种有关定义的问题,又是这种是非问题,很容易就能让人联想到利用反证法。有趣的是,不但证明一个无理数是无理数的时候我们需要用到反证法,在我们证明π是超越数这个命题的时候我们还要用到反证法。兴趣浓厚的读者可以看看这篇科普,从无理数的定义一直讲整理到π是超越数的证明:如果是真心想弄懂呢,可以把知乎上这个问题下的所有回答都看一遍,我保证你肯定能有所收获。就算不能学到实打实的数学知识,也能感悟到人外有人,天外有天嘛,说不定你还能从中找到生活中新的乐趣呢。
而根号2是无理数的证明过程大家可以参照这个博主的视频:
在这之后,无理数和有理数合称作实数,人们将实数作为一个整体,给出了实数定义和性质,并在之后成为与虚数相对的数学概念。
”现在,数轴上终于被无数个点充满了。“老师们一般会轻松写意的再加上这句话,但是,怎么填满的呢?
怎么进行第三次数系的扩充
今天我们习以为常含无理数的运算,在一开始,是如何融入之前的体系中去呢?首先要说明的是,我们是在运算法则不变的情况下进行数系的扩充的,数系的扩充又如下几条原则:
①扩充的目的:在原数集中某种运算不封闭,在扩充后的新数集中该运算封闭;
②扩充后的集合要扩大:进行的每一次扩充都是从一个较小的原数集扩充到一个较大的新数集,且使得原数集是新数集的一部分;
③保持原有的运算:进行扩充时,要使原数集中所能够进行的运算在新的数集中有意义,并且当把原数集中的数看成新数集中的数进行运算时,其结果应与它们在原数集中所得到的结果完全相同;
④扩充的最小性与唯一性:要使扩充后的新数集是原数集满足以上的①、②、③原则的最小扩充,并且该扩充是唯一的。
这些东西看起来高深莫测,我来举几个例子加深理解吧:
①封闭性是指什么呢?好比有理数运算的封闭性:有理数在四则运算下只能得到有理数,等到将数系扩充到实数以后,即实数的四则运算只能得到实数.
②这一点很好理解了嘛,例如有理数是实数的子集咯
③和我们所习惯的那样,从有理数发展到实数的时候,那加减乘除法则不还是照用嘛.
就是考试题越出越难了(这句划掉)④这就是告诉你,饭得一口口吃,如果一下从整数跳到实数,那样就会有很多数的定义和性质以及一些通性都难以寻觅
第一次数学危机的结束
经由此役,人们终于算是完全解决了第一次数学危机,第一次数学危机带来的影响是深远的,它象征着希腊数学的改变,自此走上完全不同的发展道路:
几何学的某些真理与算术无关,几何量不能完全由整数及其比来表示。反之,数却可以由几何量表示出来。整数的尊崇地位受到挑战,古希腊的数学观点受到极大的冲击。于是,几何学开始在希腊数学中占有特殊地位。同时也反映出,直觉和经验不一定靠得住,而推理证明才是可靠的。从此希腊人开始从“自明的”公理出发,经过演绎推理,并由此建立几何学体系。这是数学思想上的一次革命,是第一次数学危机的自然产物。
但是,自此以后希腊人把几何看成了全部数学的基础,把数的研究隶属于形的研究,割裂了它们之间的密切关系。这样做的最大不幸是放弃了对无理数本身的研究,使算术和代数的发展受到很大的限制,基本理论十分薄弱。这种畸形发展的局面在欧洲持续了2000多年。[3]
当然了,此后还会有第二次、第三次数学危机,他们虽然解决的问题表面上看起来并不相同,但实际上都是直指数学根本根基的问题。前人的成果推动了数学的发展,也同样为我们提供更复杂的角度,更尖锐的视角去拷问本质。用悖论提出问题,促使人们去回答,让思考一直在路上。至于提出悖论的人,例如芝诺,唔,由于篇幅原因就不赘述了。不过他的悖论也是第二次数学危机的由头呢。
π
兜兜转转说了那么多,终于讲到π了,今天是3月14日,正好是圆周率π的整数部分和它的小数点后两位,所以又称今天为π日。同时,今天也是爱因斯坦的诞辰以及霍金和马克思的忌辰。在缅怀思想家和科学家时,我们依旧不能忘记他们所留下的思想和成果,还有科学的精神,那是每一个科学家都共有的。所以,在今天,我们不妨看一看有关于π的、前人的成果。
π的定义为圆周长与圆直径之比,这使我们可以直接但不准确地对圆进行测量,抑或对其进行精确而但却毫无意义的计算。
π的发现
人们是怎么发现π的呢?我们又是怎么知道π近似于3.14...的呢
很可惜,《物理学家》杂志早在2018年8月24日发文称:
很遗憾,π的使用时间比历史上的记载时间还要早,所以,这个问题没人能解答。
π的计算史和π的计算方法
既然没有办法追究其发现,我们不如去看一看计算π的历史和一些计算方法吧。在计算π这件事的历史上,东方人还真的能和西方人打个有来有回。
祖冲之是最早计算出圆周率的人,祖冲之算出圆周率(π)的真值在3.1415926和3.1415927之间,即精确到了小数点后第7位。
除此之外,刘徽

(没错,就是那个精确定义负数的刘徽)的“割圆法”可以说是古代人解决求圆周率问题的妙计之一,就连阿基米德都使用了这种方法,可惜的是他最终死在了无名士兵的刀下,一颗巨星就此陨落......
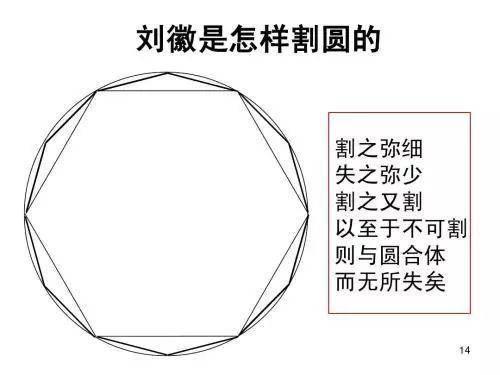
现代计算机的出现,大大加快了计算的速度,准确数字越来越多,前辈们的计算结果与现在的相比虽然不值一提,但我们不能忘记,没有他们的计算,就不会有我们的今天。
注:后面的部分会有以计算机算法在圆周率计算上的实现,所以我在此就不再赘述了。
关于π的各种不可思议
我个人嘛,是一个的忠实粉丝,在这一部分的结尾,我也不再关公面前舞大刀了,所以我整理了有关π的一些很烧脑但是又很有趣的3B1B的视频,由衷地希望各位读者们能够发自真心的感受到数学之美
[1]、[2] 西方哲学史 第九版 斯通普夫著
[3]资源来自网络
