数制（二进制、八进制、十进制）与码制（原码、反码、补码）_数制和码制-CSDN博客

前言

此篇文章是由于我对补码的概念不是很理解，而且对补码的计算方法也有很多说法，整体比较乱。所以才想着写一篇来阐述补码的用法与来历。很多书籍讲的太过于繁杂，而且还很不好理解，所以我用我认为好理解的方式来总结一下。想直接看补码请跳到2.3章节

一、数制

数制：不同数码可以表示不同数量大小，又可表示不同事物或事物不同状态。多位数码中每一位构成方法和从低位到高位的进位规则称为数制。例如十进制是逢十进一，相类似的八进制是逢八进一，二进制是逢二进一。这样的称为数制。
所有数制的数我们都可以用如下方法转换为十进制数值：
$\sum {k_iN^i}$
N：计数基数，如果是二级制这个值就是2，如果是十进制这个数就是10
$K_i$ ：第i位的系数，可以是0~9中的任意一个
$N^i$ ：第i位的权
假设整数部分位数为n、小数部分位数为m，则i包含从n-1到0的所有正整数和从-1到-m的所有负整数。即整数部分最高位为n-1，最低位为0；小数部分最高位为-1，最低位为-m。

1.1 十进制

概念：每一位有0~9十个数码，计数基数是10，超过9用多位表示，逢十进一。
计算：
$12345.67=1\times10^4 + 2\times10^3 + 3\times10^2 + 4\times10^1 + 5\times10^0 + 6\times10^{-1} + 7\times10^{-2}$
通式： $\sum {k_i10^i}$

1.2 八进制

概念：每一位都有0~7八个不同的数码，计数基数为8，逢八进一。
计算：
$(12.4)_8=1\times8^1 + 2\times8^0 + 4\times8^{-1}=(10.5)_{10}$
通式： $\sum {k_i8^i}$
脚注8和10表示括号里的数是八进制数和十进制数，有时也用O和D代替8和10

1.3 二进制

概念：每一位有0、1两个可能的数码，计数基数是2，逢二进一。
计算：
$(101.11)_2=1\times2^2 + 0\times2^1 + 1\times2^0 + 1\times2^{-1} + 1\times2^{-2}=(5.75)_{10}$
通式： $\sum {k_i8^i}$

1.4 数制转换

这里不再赘述，请参考相关文章^[1]。

二、整数在计算机中表示法

2.1 无符号整数表示法

无符号整数也就是我们常说的0和正整数（也就是0到 $+\infin$ ）。而负数前面带了符号（-）所以他属于有符号整数。

首先将整数变成二进制数。 在计算机中存储的都是二进制数故都需要转换。
如果二进位数不足n位，则在二进制整数的左边补0，使它的总位数位n位。如果位数大于n，该整数无法存储。导致溢出的情况发生。 一般在计算机中存储一个数值都是用固定长度。例如我们用8bit去存十进制 $4)_D$ 这个数值，那我们存储的值就为 $0000 0100)_B$ 。前面几个0是补的。

2.2 有符号整数表示法

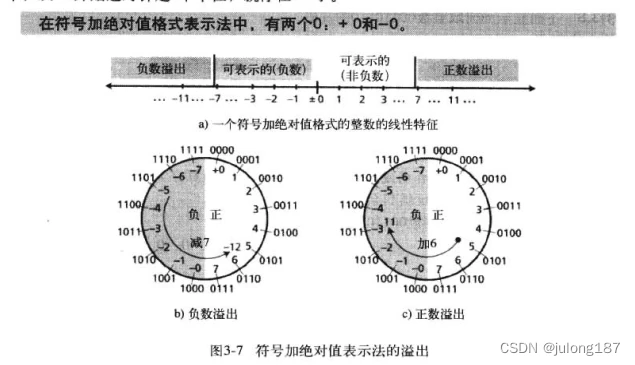
在这种方法中，用于无符号整数的有效范围(0到2ⁿ-1)被分成2个相等的子范围。前半个表示正整数，后半个表示负整数。例如:n为4，该范围是0000到1111。这个范围被分为两半:0000到0111以及1000到1111(参见图3-6)这种位模式赋值为正的和负的整数。注意，负数出现在正数的右边，与常规的关于正负数的思维相反。还要注意该系统中有两个0:正0(0000)和负0(1000)。这里跟补码有区别。
在这里插入图片描述
用符号加绝对值格式存储一个整数，需要用1个二进制位表示符号(0表示正，1表示负)。这就意味着在一个8位存储单元中，可以仅用7位表示数字的绝对值(不带符号)。因此，最大的正数值仅是无符号最大数的一半。在n位单元可存储的数字范围是-(2ⁿ-1)至+(2ⁿ-1)，n位单元中最左位分配用于存储符号(0表示正，1表示负)。 这里就涉及到一个数制和码制的概念，我们一般认为数制是可以比大小的，而码制也就是这里的最高位（最左位）代表了另外一个意义即正负。
在这里插入图片描述

2.3 有符号整数原码、反码、补码

几乎所有的计算机都使用二进制补码表示法来存储位于n位存储单元中的有符号整数。这里我们需要提前了解一下原码、反码，最后再计算补码。

2.3.1 原码

原码就是2.2章节中有符号整数使用符号加绝对值的表示方法所得到的二进制码。
最高位为符号位，0表示正数，1表示负数。

例如：
X = 0b11 (3)，四比特表示原码 = 0011(3)；
X = - 0b11(-3) ，四比特表示原码 = 1011(11)；

2.3.2 反码

2.3.2.1 反码的计算

最高位为符号位，0表示正数，1表示负数。
正数的反码等于本身，负数的反码除符号位外，各位取反（从这里我们也可以看出原码的反码的反码等于原码）：

例如：
X = 0b11 (3)，四比特表示原码 = 0011(3)，对应反码为 = 0011(3)；
X = - 0b11(-3) ，四比特表示原码 = 1011(11)，对应反码为 = 1100(12)；

上面我们所说的是通常意义上的反码，不过在有些书里面反码也指

正数的反码为正数本身
X = 0b11 (3)，四比特表示原码 = 0011(3)，对应反码为 = 0011；
负数的反码是按位取反得到的数据，因为他们认为一个整数的绝对值的二进制表示称之为原码
X = - 0b11(-3) ，四比特表示原码 = 0011(-3的绝对值为3)，对应反码为 = 1100；
注意：这种说法教科书里不常用，不建议使用。

正常我们对反码有这些了解就可以了。不过有时我们想了解一下为什么会有反码这个东西，作用是什么？

2.3.2.2 反码的意义

反码的作用就相当于数学中的负数。 3-5=3+[-5]=[-2]，中括号代表“负数”，“负数”就是我们人为给出的数学术语。对于计算机来说，会做的算术题是：5+3，但是不会做3-5。于是，我们就在编码里引进了一个新的概念：反码。引入反码之后，本来是减法的运算就可以变成加法来实现：
3-5=3+[-5]=[-2]，中括号代表“反码”，“反码”就是我们人为给出的计算机术语。
因为在计算机的数字电路中只有加法器，没有所谓的“减法器”。不是说计算机厂商不会设计减法器，因为聪明的人既然发明了方法能够用加法来实现减法操作，那为什么还需要画蛇添足的弄一个减法器？
我们御用上述所学到的方法分别计算3和[-5]的反码：

正数的反码保持原码不变：3 = [0_0000011]
负数除最高位（正负符号位）外，全部取反(0变1,1变0)：-5=1_0000101取反=[1_1111010]
于是3+[-5]=[-2]的计算过程为：
[0_0000011]+[1_1111010]=[1_1111101]
这样我们就得到了一个反码1_1111101，我们可以知道他是有符号整数1_0000010的反码，也就是[-2]

补码也有与反码相同的作用，那么有人就会问：“既然有了反码，为什么还需要补码呢？”。我们在下一章节解决这个问题。

2.3.1 补码

2.3.1.1 补码的计算

最高位为符号位，0表示正数，1表示负数。
正数的补码等于本身，负数的补码等于反码(除符号位外，各位取反)+1
有些文章里面说是数值位逐位取反+1，其实是一个意思，符号位以外的地方都是数制位

例如：
X = 0b11 (3)，四比特表示原码 = 0011(3)，对应反码为 = 0011(3) ，补码为 = 0011(3)；
X = - 0b11(-3) ，四比特表示原码 = 1011(11)，对应反码为 = 1100(12)，补码为1101(13)；

还有有些文章里面说负数的补码等于各位取反加1，因为他们认为一个整数的绝对值的二进制表示称之为原码。注：这种说法更不常用，尽量不要使用。

例如：
X = - 0b11(-3) ，四比特原码表示 = 0011（这里为-3的绝对值），补码为1101(也就是说计算的绝对值各位取反+1)；

我们用上面的方法去算就可以，其他不必理会。当然我们还有其他算法，比如用溢出的算法计算负值N的补码2ⁿ-|N|（也就是2的n次方减N的绝对值）所得到的正数，对应的原码就是负值N的补码。
正常我们对反码有这些了解就可以了。下面关于补码的不用看。

2.3.1.2 补码的意义

从上一个章节我们了解到反码的作用 – 为了应对加法器运算负数值的情况。其实补码的作用也是这个，只不过反码有一些不足，我们没法使用，所以最后用的是补码。
先问你一个问题:0是正数还是负数？你肯定会说：0既不是正数也不是负数，这是我们初中学到的数学知识。这个回答没有问题，所以以后每次碰到0，人们都不会把它当正数或负数。
那么计算机呢？计算机不同于人脑，计算机在碰到任何数字之前只根据最高位的符号位来判断正负性，“0”表示正数,“1”表示负数。
前面我们推论了为何要用反码，那么用8位二进制反码表示的正数范围： +0 —— +127；负数范围： -127 —— -0。但是，其中有两个特殊的编码会出现：

[0_0000000] = +0 （反码）
[1_1111111] = -0 （反码）

+0和-0会导致以下两个问题出现：

对于计算机来说，这是绝对不行的，因为任何数字都只能有1个编码。
使用+0还是-0计算，计算机是不知道的。一旦用-0来参加计算，很多运算结果就是错误的。

用反码计算
[+0] + [-0] = [0_0000000] + [1_1111111] = [1_1111111] = [-0] 这个我们还可以认为他是对的
[+1] + [-0] = [0_0000001] + [1_1111111] = [0_0000000] = [+0] 由于有数据溢出，我们得到的值为0，这就不是我们想要的了

我们为了保证0编码的唯一性和计算的正确性，引入了补码的概念。下面我们做一个通俗的解释：

把0当成正数，也即+0，这样0的编码就变成：0_0000000。那8位二进制表示的正数范围仍然是： +0 — +127。
对于负数就必须要做调整，也即-0必须要让位1_1111111这个编码不能表示-0。我们可以把负数整体向后“挪动1位”：只要将8位二进制表示的负数范围从：-127 — -0变成：-128 — -1，就能成功解决问题。
那么怎么整体挪动1位呢？方法就是反码+1。{1_1111111}编码就不再表示-0，而变成了-1。顺着推，最小的编码{1_0000000}就是-128。
我们给这个反码+1又人为的取了一个新的名字，叫补码。

上面的解释是我在参考文章^[3]里面看到的解释，有一定道理而且很好理解，但是数学是一个比较严谨的学科，-128的补码不仅仅是一个简单的定义，是有一个严谨的表达式的。参考清华大学的数电课程^[4]给出的补码表达式如下：
在这里插入图片描述
用这个公式我们计算两个二级制的补码对应的十进制的值：

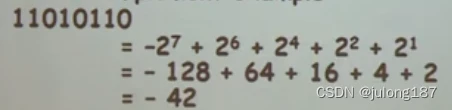
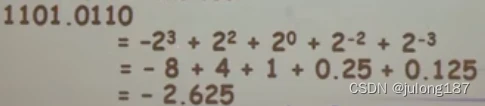
我们可以看到最高位bit代表了两个含义：
1. 最高位bit本身就带一个负号（码制：0代表正，1代表负），
2. 还代表了数值大小（数制）。
这是数制和码制的结合使用。后面我们会简单介绍一下码制。
为了证明我们已经解决了反码的不足，我们用上面-0反码[1_1111111]也就是-1[1_1111111]补码，再重新计算一次上面的例子：

反码：[+0] + [-0] = [0_0000000] + [1_1111111] = [1_1111111] = [-0] 结果还可以认为是对的
补码：[+0] + [-1] = [0_0000000] + [1_1111111] = [1_1111111] = [-1] 结果正确

反码：[+1] + [-0] = [0_0000001] + [1_1111111] = [0_0000000] = [+0] 结果错误
补码：[+1] + [-1] = [0_0000001] + [1_1111111] = [0_0000000] = [0] 结果正确

2.3.4 原码、反码、补码总结

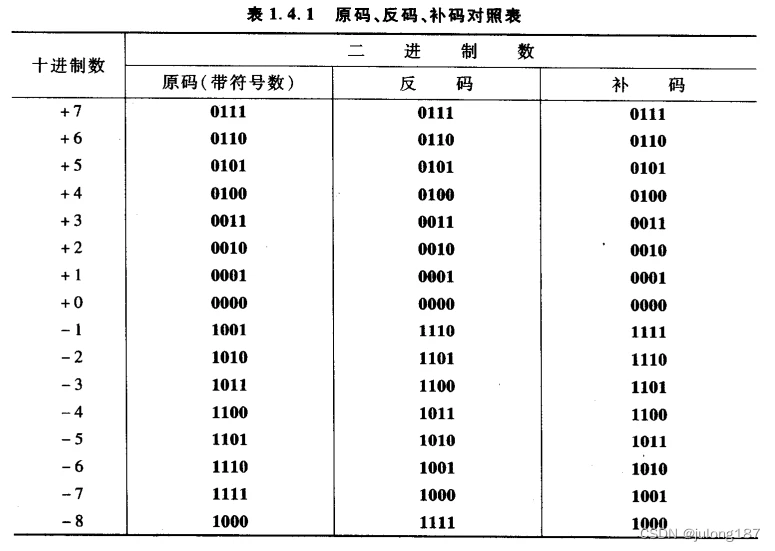
在这里插入图片描述
这里我想提一下的是原码、反码、补码定义计算方法不是一成不变的，但是最后计算出来的值和最终值的使用方法都是相同的。有兴趣的可以看看《计算机科学导论》佛罗赞著。这里面对反码和补码有不一样的定义和计算，（一般概念上述就够了，下面不用看，容易混淆）。

他认为反码和补码只是通过特定运算方式得到的二进制数，不会区分正数还是负数。像我们上面讲的正数的反码和补码与原码相同，他不是这么认为。举个例子：

我们认为计算机存的是正数的补码和负数的补码。
而《计算机科学导论》这本书的认为正数是直接存在计算机存储器中的认为他是补码，而负数是以补码运算之后的二进制形式存储在存储器中的。

这里看似好像最终结果都是一样的，但是这对反码和补码的计算公式有很大影响，因为他计算反码和补码的时候不会去判断正负号了，他认为原码是无符号整数：

原码的定义：
我们认为-3的4bit原码是0b1011，是有符号整型
而他认为-3的4bit原码是0b0011，是一个无符号整型，是原值的绝对值

反码的计算：
我们认为原码是有符号整数，反码是符号位不变，其他位逐位取反。-3的4bit原码是0b1011，反码是最高位不变，其他位取反结果是0b1100
而他认为原码是无符号整型，反码是所有位按位取反。-3的4bit原码是0b0011，所有位按位取反的结果是0b1100。他认为3的反码也是0b1100（实际上就是一个按位取反的操作）
我们看似结果好像都是一样的，但我们要是把他运用到计算中就不同了。

补码的计算：
这里还是比较统一的，都认为补码是反码 + 1

这使得在加减运算的过程中所使用的公式不一样《计算机科学导论》认为

这里就用了他所说的补码计算方式B的反码（按位取反）加1，他没有去管B值的符号位。
如果按照我们的计算方式来用公式就有问题。

三、码制

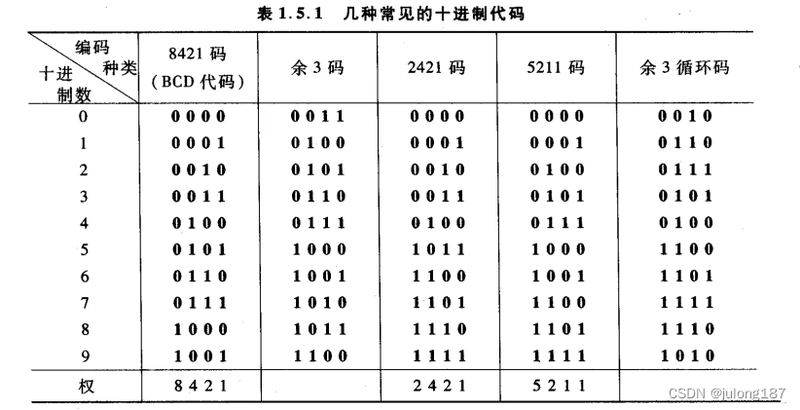
码制：当数码表示不同事物或事物不同状态时，数码成为了不同事物的代号，称为代码。编制代码时遵循的一定规则称为码制。例如ASCII码可以对应字符，8421码对应数字等。
为了用二进制代码表示十进制数的0~9这十个状态,二进制代码至少应当有4位。4位二进制代码一共有十六个(0000~1111)，取其中哪十个以及如何与0~9相对应,有许多种方案。下表中列出了常见的几种十进制代码，它们的编码规则各不相同。
在这里插入图片描述

参考文章

数电基础：数制与码制
补码的计算方法
为什么计算机要使用反码/补码
清华数电课程--信息与编码