常微分方程这部分内容,每年都会考察,也会和其它知识点结合在一起出一个大题,分数一般在4分左右,难度不是很大。除了各种微分方程的求解,对常系数线性微分方程解的结构和性质的考查也是考试的一个重要方面。下面总结一下一些二阶及高阶微分方程的种类及其解法,希望对正在备考2020年考研和即将备考同学们有些帮助。
(1)二阶线性微分方程

(2)二阶常系数线性微分方程

(3)二阶常系数非齐次线性微分方程

(4)高于二阶的某些常系数齐次线性微分方程
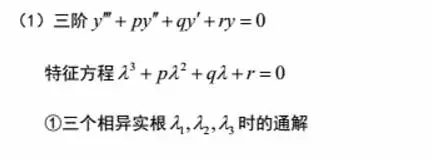


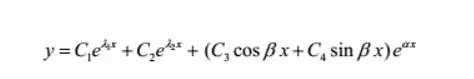
题型一:已知通解确定微分方程的形式
例1:(2018年考研真题)
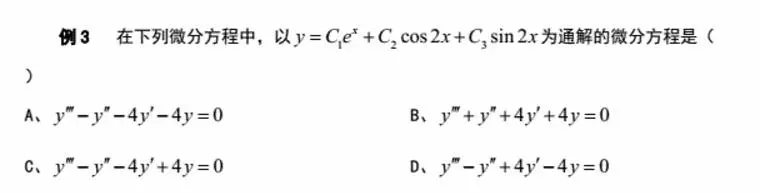
分析:通过通解的形式可以得到微分方程的特征根。
解:

题型二:高阶齐次线性微分方程的求解
例2:(2010考研真题)
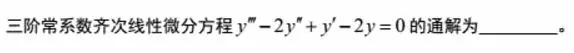
分析:写出微分方程的特征方程,求出特征方程的特征根。
解:

题型三:二阶非齐次线性微分方程的求解
例3:(2007年真题)

解题思路:
第一步:写出对应的齐次微分方程的通解Y(x)
第二步:求该非齐次微分方程的特解
解:

