文章转载请注明出处,加上原文地址链接,谢谢!
文章目录
前言
矩阵对角化一节略有琐碎,对于如何判断矩阵对角化——代数重数和几何重数相等,笔者已经在第五篇线代笔记中给出了相应的定义以及数学层面的证明。在第六篇笔记中笔者将对矩阵的对角化给出粗略的梳理,涉及定义、矩阵对角化相应的例题(经典斐波那契数里的通项求解、MIT线代习题公开课T23求矩阵的方幂、MIT线代习题公开课T25粒子的跳跃)以及相应的结论。对于对角化一节会粗粗略过,该篇重点回放在第二部分——特征值在微分方程中的应用。对上一篇笔记有印象的朋友肯定会记得,笔者在已经给出一个常系数微分方程的例题。在这里笔者会涉及更多的东西,如以微分方程的角度探讨矩阵对角化的情形,从指数函数的层面推出矩阵 e A t e^{At} eAt 的导数公式,最后给出微分方程解的稳定性分析以及归纳图。下面我们正式开始。
矩阵对角化的定义
定义 如果n阶矩阵A有n个线性无关的特征向量 ( v 1 , ⋯ , v n ) , \mathsf{(v_1,\cdots,v_n)}, (v1,⋯,vn), 令 S = ( v 1 , v 2 , ⋯ , v n ) , \mathsf{S=(v_1,v_2,\cdots,v_n)}, S=(v1,v2,⋯,vn), 则有 A S = S ( λ 1 λ 2 ⋱ λ n ) = S Λ \mathsf{AS=S\begin{pmatrix}\lambda_1& & \\ &\lambda_2& \\ & & \ddots& \\ & & &\lambda_n\\\end{pmatrix}=S\Lambda} AS=S λ1λ2⋱λn =SΛ故 S − 1 A S = Λ \mathsf{S^{-1}AS=\Lambda} S−1AS=Λ 为对角阵。此时称矩阵 A \mathsf{A} A可对角化。
光有定义印象还不够深刻,下面笔者引用经典的斐波那契数列的通项和两道MIT线代习题课内的两道题帮助大家加深印象。对于已经熟悉的朋友快速过一篇例题,略有生涩的朋友可以点击链接,跳转观看讲解视频。
对角化应用例题方面的分析
|经典的斐波那契数列求通项
题 求斐波那契数列 0 , 1 , 1 , 2 , 3 , 5 , 8 ⋯ \mathsf{0,1,1,2,3,5,8\cdots} 0,1,1,2,3,5,8⋯ 的通项?
解: 令 u k = ( F k + 1 F k ) , \mathsf{u_k=\begin{pmatrix}F_{k+1}\\F_k\\\end{pmatrix}}, uk=(Fk+1Fk), 推敲数列前后两项可得 { F k + 2 = F k + 1 + F k F k + 1 = F k + 1 \mathsf{\begin{cases}F_{k+2}=F_{k+1}+F_k\\F_{k+1}=F_{k+1}\\\end{cases}} {Fk+2=Fk+1+FkFk+1=Fk+1则 u k + 1 \mathsf{u_{k+1}} uk+1 矩阵的形式为 u k + 1 = ( 1 1 1 0 ) u k ⟶ A u k = u k + 1 \mathsf{u_{k+1}=\begin{pmatrix}1&1\\1&0\\\end{pmatrix}u_k\longrightarrow Au_k=u_{k+1}} uk+1=(1110)uk⟶Auk=uk+1 故有 d e t ( A − λ I ) = ∣ 1 − λ 1 1 − λ ∣ = λ 2 − λ − 1 = 0 \mathsf{det(A-\lambda I)=\begin{vmatrix}{1-\lambda}&{1}\\{1}&{-\lambda}\\\end{vmatrix}=\lambda^2-\lambda-1=0} det(A−λI)= 1−λ11−λ =λ2−λ−1=0 解得 λ 1 = 1 + 5 2 , λ 2 = 1 − 5 2 < 0 \mathsf{\lambda_1=\frac{1+\sqrt5}{2},\lambda_2=\frac{1-\sqrt5}{2}\lt 0} λ1=21+5,λ2=21−5<0 故通项 F n = C 1 ( 1 + 5 2 ) n + C 2 ( 1 − 5 2 ) n \mathsf{F_n=C_1(\frac{1+\sqrt5}{2})^n+C_2(\frac{1-\sqrt5}{2})^n} Fn=C1(21+5)n+C2(21−5)n
因通项的后半段中 1 − 5 2 < 0 , \mathsf{\frac{1-\sqrt5}{2}\lt0}, 21−5<0, 故无穷后趋向于零。这里有一个非常深刻的地方,为什么一个全部是有理数的数列,其数列的通项推导出来会有无理数被包含在内呢? 这里笔者对于数论并没有研究,无法深入探讨,阅读的朋友可以自行挖掘。
|矩阵方幂的求取——MIT线代习题课 T23
教学视频链接 https://www.bilibili.com/video/BV19b411E7ue?p=23
题 对矩阵 C = ( 2 b − a a − b 2 b − 2 a 2 a − b ) , \mathsf{C=\begin{pmatrix}{2b-a}&{a-b}\\{2b-2a}&{2a-b}\\\end{pmatrix}}, C=(2b−a2b−2aa−b2a−b), 并计算当 a = b = − 1 \mathsf{a=b=-1} a=b=−1 时,求取 C 100 \mathsf{C^{100}} C100。
解:
d e t ( C − λ I ) = d e t ∣ ( 2 b − a ) − λ a − b 2 b − 2 a ( 2 a − b ) − λ ∣ = ( λ − a ) ( λ − b ) = 0 \mathsf{det(C-\lambda I)=det\begin{vmatrix}{(2b-a)-\lambda}&{a-b}\\{2b-2a}& {(2a-b)-\lambda}\\\end{vmatrix}=(\lambda-a)(\lambda-b)=0} det(C−λI)=det (2b−a)−λ2b−2aa−b(2a−b)−λ =(λ−a)(λ−b)=0 解,得 λ 1 = a , λ 2 = b \mathsf{\lambda_1=a,\lambda_2=b} λ1=a,λ2=b
对应特征值
λ
1
=
a
\mathsf{\lambda_1=a}
λ1=a 特征向量
v
1
\mathsf{v_1}
v1 的计算:
(
c
−
a
I
)
v
1
=
(
2
b
−
2
a
a
−
b
2
b
−
2
a
a
−
b
)
v
1
=
0
→
v
1
=
(
1
2
)
\mathsf{(c-aI)v_1=\begin{pmatrix}{2b-2a}&{a-b}\\{2b-2a}&{a-b}\\\end{pmatrix}v_1=0 \rightarrow v_1=\begin{pmatrix}1\\2\\\end{pmatrix}}
(c−aI)v1=(2b−2a2b−2aa−ba−b)v1=0→v1=(12)
对应特征值
λ
2
=
b
\mathsf{\lambda_2=b}
λ2=b 特征向量
v
2
\mathsf{v_2}
v2 的计算:
( c − b I ) v 2 = ( b − a a − b 2 b − 2 a 2 a − 2 b ) v 2 = 0 → v 2 = ( 1 1 ) \mathsf{(c-bI)v_2=\begin{pmatrix}{b-a}&{a-b}\\{2b-2a}&{2a-2b}\\\end{pmatrix}v_2=0 \rightarrow v_2=\begin{pmatrix}1\\1\\\end{pmatrix}} (c−bI)v2=(b−a2b−2aa−b2a−2b)v2=0→v2=(11)
故特征向量矩阵 S = ( 1 1 2 1 ) , \mathsf{S=\begin{pmatrix}1&1\\2&1\\\end{pmatrix}}, S=(1211), 其逆矩阵 S − 1 = 1 d e t S ( S i j ) T = ( − 1 1 2 − 1 ) , \mathsf{S^{-1}=\frac{1}{det S}(S_{ij})^T=\begin{pmatrix}-1&1\\2&-1\\\end{pmatrix}}, S−1=detS1(Sij)T=(−121−1),
则有 C = S − 1 Λ S = ( 1 1 2 1 ) ( a b ) ( − 1 1 2 − 1 ) \mathsf{C=S^{-1}\Lambda S=\begin{pmatrix}1&1\\2&1\\\end{pmatrix}\begin{pmatrix}a& \\ &b\\\end{pmatrix}\begin{pmatrix}-1&1\\2&-1\\\end{pmatrix}} C=S−1ΛS=(1211)(ab)(−121−1)
所以
C
k
=
S
−
1
Λ
K
S
=
(
1
1
2
1
)
(
a
K
b
K
)
(
−
1
1
2
−
1
)
=
(
2
b
k
−
a
k
a
K
−
b
k
2
b
K
−
2
a
K
2
a
K
−
b
K
)
\mathsf{C^k=S^{-1}\Lambda^K S=\begin{pmatrix}1&1\\2&1\\\end{pmatrix}\begin{pmatrix}a^K& \\ &b^K\\\end{pmatrix}\begin{pmatrix}-1&1\\2&-1\\\end{pmatrix}=\begin{pmatrix}{2b^k-a^k}&{a^K-b^k}\\{2b^K-2a^K}&2a^K-b^K\\\end{pmatrix}}
Ck=S−1ΛKS=(1211)(aKbK)(−121−1)=(2bk−ak2bK−2aKaK−bk2aK−bK)
故
C
100
=
S
Λ
100
S
−
1
=
(
1
0
0
1
)
=
I
\mathsf{C^{100}=S\Lambda^{100}S^{-1}=\begin{pmatrix}1&0\\0&1\\\end{pmatrix}=I}
C100=SΛ100S−1=(1001)=I
想必仔细阅读下来的朋友可以理解矩阵的对角化对于求幂次矩阵的的强大威力。注意 ( S i j ) T (S_{ij})^T (Sij)T 是代数余子式矩阵的转置矩阵。
|马尔可夫矩阵计算粒子跳跃——MIT线代习题课T25
教学视频链接 https://www.bilibili.com/video/BV19b411E7ue?p=25

矩阵对角化的结论
- 矩阵A可对角化,值存在可逆矩阵S,使 S − 1 A S = Λ \mathsf{S^{-1}AS=\Lambda} S−1AS=Λ 为对角阵且 A k = S Λ k S − 1 \mathsf{A^k=S\Lambda^kS^{-1}} Ak=SΛkS−1;
- n × n n\times n n×n 矩阵对角化 ⟷ \longleftrightarrow ⟷A有n个线性无关的特征向量;
- n × n n\times n n×n 复矩阵A有n个互异特征值,则A可对角化;
- n × n n\times n n×n 复矩阵A可对角化 ⟷ \longleftrightarrow ⟷任意特征值的几何重数等于代数重数;
- 差分方程 u k + 1 = A u k \mathsf{u_{k+1}=Au_k} uk+1=Auk的解为 u k = A k u 0 = S Λ k S − 1 u 0 = c 1 λ 1 k x 1 + ⋯ + c n λ n k x n , \mathsf{u_k=A^ku_0=S\Lambda^kS^{-1}u_0=c_1\lambda_1^kx_1+\cdots+c_n\lambda_n^kx_n}, uk=Aku0=SΛkS−1u0=c1λ1kx1+⋯+cnλnkxn,其中 u 0 = c 1 x 1 + ⋯ + c n x n , A x i = λ i x i ( 1 ≤ i ≤ n ) . \mathsf{u_0=c_1x_1+\cdots+c_nx_n,Ax_i=\lambda_ix_i(1\le i \le n)}. u0=c1x1+⋯+cnxn,Axi=λixi(1≤i≤n).
矩阵的指数函数形式
对于 e x = ∑ n = 0 ∞ = 1 + x + x 2 2 ! ⋯ + x n n ! + ⋯ \mathsf{e^x=\displaystyle\sum_{n=0}^{\infty}=1+x+\frac{x^2}{2!}\cdots+\frac{x^n}{n!}+\cdots} ex=n=0∑∞=1+x+2!x2⋯+n!xn+⋯ 推出 e A t = I + A t + ( A t ) 2 2 ! ⋯ + ( A t ) n n ! + ⋯ \mathsf{e^{At}=I+At+\frac{(At)^2}{2!}\cdots+\frac{(At)^n}{n!}+\cdots} eAt=I+At+2!(At)2⋯+n!(At)n+⋯ 推出 d ( e A t ) d t = A + A 2 t + A 3 t 2 2 ! + ⋯ = A ( I + A t + ( A t ) 2 2 ! + ⋯ ) = A e A t \mathsf{\frac{d(e^{At})}{dt}=A+A^2t+\frac{A^3t^2}{2!}+\cdots=A(I+At+\frac{(At)^2}{2!}+\cdots)=Ae^{At}} dtd(eAt)=A+A2t+2!A3t2+⋯=A(I+At+2!(At)2+⋯)=AeAt 推出 u ( t ) = e A t u ( 0 ) 为 d u d t = A u 的解 \mathsf{u(t)=e^{At}u(0)为 \frac{du}{dt}=Au的解} u(t)=eAtu(0)为dtdu=Au的解
|矩阵的指数函数性质
- 如果 Λ = ( λ 1 ⋱ λ n ) , \mathsf{\Lambda=\begin{pmatrix}\lambda_1& & \\ &\ddots& \\ & &\lambda_n\\\end{pmatrix}}, Λ= λ1⋱λn , 则 e Λ t = ( e λ 1 t ⋱ e λ n t ) = ( 1 + λ 1 t + ( λ 1 t ) 2 2 ! + ⋯ + ( λ 1 t ) n n ! + ⋯ ⋱ 1 + λ n t + ( λ n t ) 2 2 ! + ⋯ + ( λ n t ) n n ! ⋯ ) \mathsf{e^{\Lambda t}=\begin{pmatrix}e^{\lambda_1t}& & \\ &\ddots& \\ & &e^{\lambda_nt}\\\end{pmatrix}=\begin{pmatrix}1+\lambda_1t+\frac{(\lambda_1t)^2}{2!}+\cdots+\frac{(\lambda_1t)^n}{n!}+\cdots\\ &\ddots& \\ & &1+\lambda_nt+\frac{(\lambda_nt)^2}{2!}+\cdots+\frac{(\lambda_nt)^n}{n!}\cdots\\\end{pmatrix}} eΛt= eλ1t⋱eλnt = 1+λ1t+2!(λ1t)2+⋯+n!(λ1t)n+⋯⋱1+λnt+2!(λnt)2+⋯+n!(λnt)n⋯
- 如果 A B = B A , \mathsf{AB=BA}, AB=BA, 则 e A + b = e A ∗ e B , \mathsf{e^{A+b}=e^A*e^B}, eA+b=eA∗eB, 特别有 ( e A ) − 1 = e − A \mathsf{(e^A)^{-1}=e^{-A}} (eA)−1=e−A 且 e A + B = I + ( A + B ) + ( A + B ) 2 2 ! + ⋯ \mathsf{e^{A+B}=I+(A+B)+\frac{(A+B)^2}{2!}+\cdots} eA+B=I+(A+B)+2!(A+B)2+⋯ e A B = ( I + A + A 2 2 ! + ⋯ ) ( I + B + B 2 2 ! + ⋯ ) \mathsf{e^{AB}=(I+A+\frac{A^2}{2!}+\cdots)(I+B+\frac{B^2}{2!}+\cdots)} eAB=(I+A+2!A2+⋯)(I+B+2!B2+⋯)
- 如果存在可逆矩阵P使
A
=
P
B
P
−
1
,
\mathsf{A=PBP^{-1}},
A=PBP−1, 则
e
A
t
=
e
P
B
P
−
1
t
\mathsf{e^{At}=e^{PBP^{-1}t}}
eAt=ePBP−1t
且 e A t = e P B P − 1 T = I + P B P − 1 t + ( P B P − 1 ) 2 2 ! + ⋯ = P ( I + B t + ( B t ) 2 2 ! + ⋯ ) P − 1 \mathsf{e^{At}=e^{PBP^{-1}T}=I+PBP^{-1}t+\frac{(PBP^{-1})^2}{2!}+\cdots=P(I+Bt+\frac{(Bt)^2}{2!}+\cdots)P^{-1}} eAt=ePBP−1T=I+PBP−1t+2!(PBP−1)2+⋯=P(I+Bt+2!(Bt)2+⋯)P−1
特征值在微分方程中的应用
一般地,如果 A = S Λ S − 1 \mathsf{A=S\Lambda S^{-1}} A=SΛS−1可对角化,类似于求解 u k = A k u 0 , \mathsf{u_k=A^ku_0}, uk=Aku0, 有 d u d t = A u = S Λ S − 1 u ⟺ d ( S − 1 u ) d t = Λ ( S − 1 u ) , \mathsf{\frac{du}{dt}=Au=S\Lambda S^{-1}u \Longleftrightarrow \frac{d(S^{-1}u)}{dt}=\Lambda(S^{-1}u)}, dtdu=Au=SΛS−1u⟺dtd(S−1u)=Λ(S−1u), 即 S − 1 u = ( e λ 1 t C 1 e λ 2 t C 2 ⋮ e λ n t C n ) → u ( t ) = C 1 e λ 1 t x 1 + ⋯ + C n e λ n t x n \mathsf{S^{-1}u=\begin{pmatrix}e^{\lambda_1t}C_1\\e^{\lambda2t}C_2\\\vdots\\e^{\lambda_nt}C_n\\\end{pmatrix}\rightarrow u(t)=C_1e^{\lambda_1t}x_1+\cdots+C_ne^{\lambda_n}tx_n} S−1u= eλ1tC1eλ2tC2⋮eλntCn →u(t)=C1eλ1tx1+⋯+Cneλntxn 同时,对于 d u d t = A n × n u \mathsf{\frac{du}{dt}=A_{n\times n}u} dtdu=An×nu 的解集是一个n维向量空间。如果A可对角化,则 d u d t = A u \mathsf{\frac{du}{dt}=Au} dtdu=Au 的解空间有一组基 { e λ 1 t x 1 , e λ 2 t x 2 ⋯ , e λ n t x n } \mathsf{\lbrace e^{\lambda_1t}x_1,e^{\lambda_2t}x_2\cdots,e^{\lambda_nt}x_n\rbrace} {eλ1tx1,eλ2tx2⋯,eλntxn}
上述给出了微分方程层面出发的对角化,下面我们来看看特征值与二阶微分方程关系。
二阶常系数线性微分方程
设 y = e λ t \mathsf{y=e^{\lambda t}} y=eλt 是二阶微分方程 y ′ ′ + a y ′ + b y = 0 \mathsf{y''+ay'+by=0} y′′+ay′+by=0 的解,则有 λ 2 + a λ + b = 0 \mathsf{\lambda^2+a\lambda+b=0} λ2+aλ+b=0。如果解 λ 1 ≠ λ 2 , \mathsf{\lambda_1\neq \lambda_2}, λ1=λ2, 则 y 1 = e λ 1 t , y = e λ 2 t \mathsf{y_1=e^{\lambda_1t},y=e^{\lambda_2t}} y1=eλ1t,y=eλ2t 为两个线性无关的解,以下:
- 若 λ 1 , λ 2 \mathsf{\lambda_1,\lambda_2} λ1,λ2 为实数,则方程的通解为 y = C 1 e λ 1 t + C 2 e λ 2 t ; \mathsf{y=C_1e^{\lambda_1t}+C_2e^{\lambda_2t}}; y=C1eλ1t+C2eλ2t;
- 若
λ
1
,
λ
2
\mathsf{\lambda_1,\lambda_2}
λ1,λ2 为共轭复数,即
{ λ 1 = α + i β λ 2 = α − i β \mathsf{\left \{ \begin{array}{c} \lambda_1=\alpha+i\beta\\ \lambda_2=\alpha-i\beta\\ \end{array} \right.} {λ1=α+iβλ2=α−iβ
方程组的解为
y = e α t ( C 1 cos β t + C 2 sin β t ) \mathsf{y=e^{\alpha t}(C_1\cos\beta t+C_2\sin\beta t)} y=eαt(C1cosβt+C2sinβt)
欧拉公式:
e ( α + i β ) + e ( α − i β ) 2 = e α t cos β t \mathsf{\frac{e^{(\alpha+i\beta)}+e^{(\alpha-i\beta)}}{2}=e^{\alpha t}\cos\beta t} 2e(α+iβ)+e(α−iβ)=eαtcosβt e ( α + i β ) − e ( α − i β ) 2 = e α t sin β t \mathsf{\frac{e^{(\alpha+i\beta)}-e^{(\alpha-i\beta)}}{2}=e^{\alpha t}\sin\beta t} 2e(α+iβ)−e(α−iβ)=eαtsinβt
博客修改失误,图片彻底消失。😳
图片链接格式中瑕疵修改完毕,图片顺利显示。(2022.5.7 23:14)

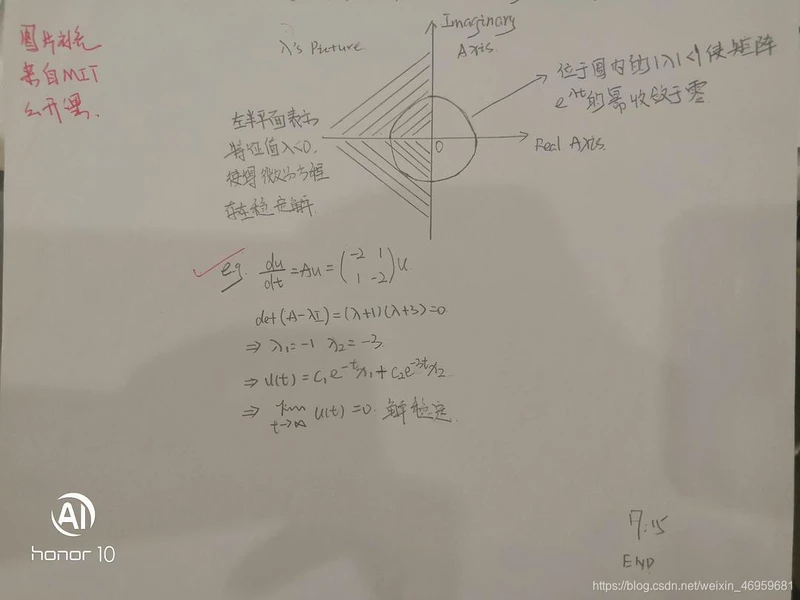
|微分方程 d u d t = A u \mathsf{\frac{du}{dt}=Au} dtdu=Au 的解的稳定性的分析及归纳图
t ⟶ ∞ \mathsf{t\longrightarrow \infty} t⟶∞ 时, A \mathsf{A} A 的特征值决定解 u ( t ) u(t) u(t) 的稳定性。若 A \mathsf{A} A 可对角化,则 d u d t = A u \mathsf{\frac{du}{dt}=Au} dtdu=Au 有通解, u ( t ) = ( x 1 , ⋯ , x n ) ( e λ 1 t ⋱ e λ n t ) ( C 1 ⋮ C n ) \mathsf{u(t)=(x_1,\cdots,x_n)\begin{pmatrix}e^{\lambda_1t}& & \\\ & \ddots& \\ & &e^{\lambda_nt}\\\end{pmatrix}\begin{pmatrix}C_1\\\vdots\\C_n\\\end{pmatrix}} u(t)=(x1,⋯,xn) eλ1t ⋱eλnt C1⋮Cn
- 若所有 R e λ i < 0 \mathsf{Re\lambda_i \lt 0} Reλi<0,则 e A t → 0 \mathsf{e^{At}\rightarrow0} eAt→0 解时稳定的;
- 若所有 R e λ i ≤ 0 \mathsf{Re\lambda_i \le 0} Reλi≤0,则 e A t \mathsf{e^{At}} eAt 有界,解是中性的;
- 若至少有一个特征值满足 R e > 0 \mathsf{Re\gt 0} Re>0 ,则 e A t e^{At} eAt 无界,解不稳定。
对于解的稳定性分析,我们可以归纳成下面的一张图片:
参考资料
- 笔者个人清华大学线性代数公开课笔记
- 笔者个人MIT线性代数公开课笔记
- 笔者个人MIT线性代数习题公开课笔记
文章更新时间记录
- 文章版式微微调整。「2020.6.1 21:22」
- 文章版式巨大调整。「2021.3.5 18:35」
- 文章图片链接格式修改完毕,顺利显示。 「2022.5.7 23:14」
- 修改标题。「2022.11.5 9:57」
- 公开阅读权限。「2023.2.17 16:25」
P.S.1 笔者在该篇笔记的归纳整理的过程中感觉异常的不顺畅,相信通读下来的朋友应该或多或少感觉该篇有强行总结的感觉——尤其是第二部分特征值与微分方程的关系。在行文中这种感觉始终摆脱不得,最后文章成形颇有四不像的感觉,勉强看看吧。耕耘不易,有得请点赞,谢谢🙏!
