ACM 选手图解 LeetCode 删除二叉搜索树中的节点(递归 + 非递归)
持续创作,加速成长!这是我参与「掘金日新计划 · 6 月更文挑战」的第7天,点击查看活动详情
大家好呀,我是删除蛋。
今天解决删除二叉搜索树中的节点,解决完今天这道题,我在二叉搜索树入门文章中讲的二叉搜索树的 3 大操作:查找、插入和删除至此全部讲完。
坚持就是胜利,搞搞搞!
LeetCode 450:删除二叉搜索树中的节点
题意
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜素树(有可能被更新)的根节点的引用。
示例
输入:root = [5,3,6,2,4,null,7],key = 3
输出:[5,4,6,2,null,null,7]
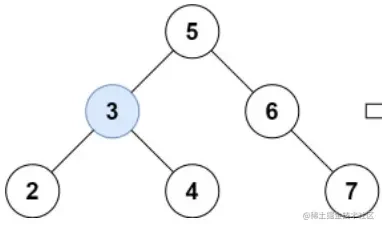
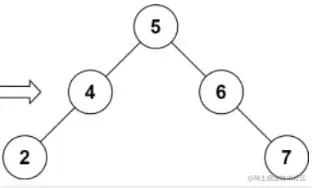
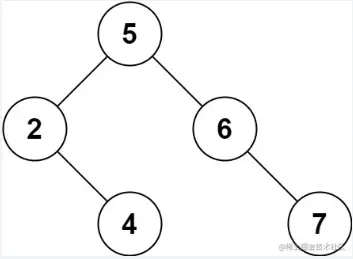
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。一个正确的答案是
[5,4,6,2,null,null,7],另一个正确答案是 [5,2,6,null,4,null,7]。
提示
- 节点数的范围 [0, 10^4]
- -10^5 <= Node.val <= 10^5
- 节点值唯一
- root 是合法的二叉搜索树
- -10^5 <= key <= 10^5
题目解析
删除二叉搜索树中的节点,难度中等,它难就难在删除节点之后仍然要保持剩下的二叉树依然是二叉搜索树。
关于删除操作我也早在下面这篇文章中讲过了:
ACM 选手带你玩转二叉搜索树!
说实话,删除操作是二叉搜索树 3 大操作中最麻烦的一个,麻烦就麻烦在涉及的情况众多,主要有 3 种:
情况 1:删除节点为二叉树的叶子节点。
这种情况很好处理,通过二叉搜索树的查找操作找到节点,然后直接删掉就好了。
删掉叶子节点对二叉树的其它节点没有什么影响。
比如对于下图:
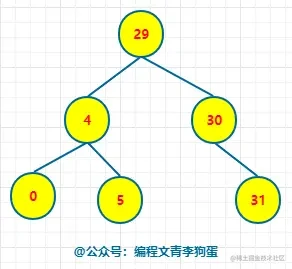
我们此时要删除 node = 0 的节点,查找到该节点,然后直接删除。
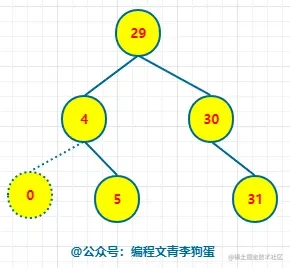
情况 2 :删除的节点只有左子树或者右子树。
碰到这种情况也比较好解决,那就是直接用删除节点的父节点指向它的子树即可。
比如对于下图:

我们此时要删除 node = 30 的节点,查找到该节点,然后删除后,二叉搜索树的变化如下所示:
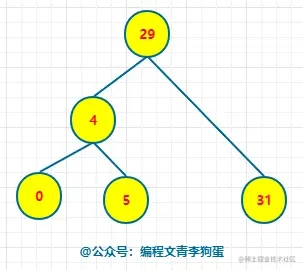
情况 3:删除的节点既有左子树又有右子树。
这个就稍微复杂点了,过程我就略过了,也不是很重要,直接说答案:
就是将要删除节点 node 位置上替换成左子树最右边的节点或者右子树最左边的节点。
即左子树的最大值或者右子树的最小值。
比如对于下图:

我们此时要删除 node = 4 的节点,它的左子树的最大值为 0,右子树的最小值为 5。
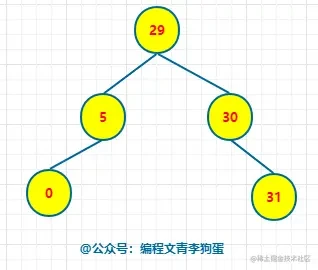
所以删除完 node = 4 后,二叉搜索树可以变成下面这样:
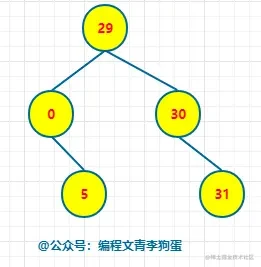
递归法
还是根据【递归算法】文章中讲的,实现递归,需要两步:
- 找出重复的子问题(递推公式)。
- 终止条件。
(1) 找出重复的子问题。
这个首先就是在二叉搜索树中找到 key 值的节点:
- 如果 key 值比当前节点的值小,那就去左子树继续找
- 如果 key 值比当前节点的值大,那就去右子树继续找
# 如果要删除的节点 key 比 root 小
if root.val > key:
# 继续在左子树寻找
root.left = self.deleteNode(root.left, key)
# 如果要删除的节点 key 比 root 大
elif root.val < key:
# 继续在右子树寻找
root.right = self.deleteNode(root.right, key)
当找到了要删除的 key 值节点,当这个节点既有左子树又有右子树的时候,一般将将要删除节点 node 位置上替换成左子树最右边的节点或者右子树最左边的节点。
然后再删除这个左子树最右边的节点或者右子树最左边的节点,这个删除节点的过程,相当于又是一个递归调用的过程。
# 情况 3:如果 key 左右子树都有,此处将 key 位置的值替换成右子树的最小值
node = root.right
while node.left:
node = node.left
root.val = node.val
# 删除右子树的最小值
root.right = self.deleteNode(root.right, node.val)
(2) 确定终止条件。
对于终止条件就没啥好说的,遍历的节点为空,直接就返回。
# 如果节点为空,直接返回
if root == None:
return None
这两点确定好了,基本上主要的代码就出来了。
Python 代码实现
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
# 如果节点为空,直接返回
if root == None:
return None
# 如果要删除的节点 key 比 root 小
if root.val > key:
# 继续在左子树寻找
root.left = self.deleteNode(root.left, key)
# 如果要删除的节点 key 比 root 大
elif root.val < key:
# 继续在右子树寻找
root.right = self.deleteNode(root.right, key)
# 如果找到了要删除的节点 key
else:
# 情况 1:如果 key 是叶子节点,直接删除
if root.left == None and root.right == None:
root = None
return root
# 情况 2:如果 key 只有左子树
elif root.left != None and root.right == None:
return root.left
# 情况 2:如果 key 只有右子树
elif root.left == None and root.right != None:
return root.right
# 情况 3:如果 key 左右子树都有,此处将 key 位置的值替换成右子树的最小值
else:
node = root.right
while node.left:
node = node.left
root.val = node.val
# 删除右子树的最小值
root.right = self.deleteNode(root.right, node.val)
return root
Java 代码实现
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
// 如果节点为空,直接返回
if(root == null){
return null;
}
// 如果要删除的节点 key 比 root 小
if(root.val > key){
root.left = deleteNode(root.left, key);
}
// 如果要删除的节点 key 比 root 大
else if(root.val < key){
root.right = deleteNode(root.right, key);
}
// 如果找到了要删除的节点 key
else{
// 情况 1:如果 key 是叶子节点,直接删除
if(root.left == null && root.right == null){
root = null;
return root;
}
// 情况 2:如果 key 只有左子树
else if(root.left != null && root.right == null){
return root.left;
}
// 情况 2:如果 key 只有右子树
else if(root.left == null && root.right != null){
return root.right;
}
// 情况 3:如果 key 左右子树都有,此处将 key 位置的值替换成右子树的最小值
else{
TreeNode node = root.right;
while(node.left != null){
node = node.left;
}
root.val = node.val;
// 删除右子树的最小值
root.right = deleteNode(root.right, node.val);
}
}
return root;
}
}
本题解,最坏情况下二叉搜索树的高度为 n,查找节点的最坏时间复杂度为 O(n),删除节点的最坏时间复杂度也为 O(n),所以最终的时间复杂度为 O(n) 。
此外在递归过程中调用了额外的栈空间,栈的大小取决于二叉搜索树的高度,同样二叉搜索树最坏情况下的高度为 n,所以空间复杂度为 O(n) 。
非递归法(迭代)
非递归法其实就没啥好多说的,就按照我在上面“题目解析”中说的几种情况进行模拟即可。
具体代码放在下面了。

Python 代码实现
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def deleteOneNode(self, root):
if root.left == None and root.right == None:
root = None
return root
elif root.left != None and root.right == None:
return root.left
elif root.left == None and root.right != None:
return root.right
else:
node = root.right
while node.left:
node = node.left
node.left = root.left
return root.right
def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
if root == None:
return None
cur = root
# 记录 cur 节点的父节点
pre = None
while cur:
if cur.val == key:
break
pre = cur
if cur.val > key:
cur = cur.left
else:
cur = cur.right
# 如果只有一个根节点
if pre == None:
return self.deleteOneNode(cur)
# 要删除的 key 在左孩子
if pre.left != None and pre.left.val == key:
pre.left = self.deleteOneNode(cur)
# 要删除的 key 在右孩子
if pre.right != None and pre.right.val == key:
pre.right = self.deleteOneNode(cur)
return root
Java 代码实现
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode deleteOneNode(TreeNode root){
if(root.left == null && root.right == null){
root = null;
return root;
}
else if(root.left != null && root.right == null){
return root.left;
}
else if(root.left == null && root.right != null){
return root.right;
}
else{
TreeNode node = root.right;
while(node.left != null){
node = node.left;
}
node.left = root.left;
return root.right;
}
}
public TreeNode deleteNode(TreeNode root, int key) {
if(root == null){
return null;
}
TreeNode cur = root;
// 记录 cur 节点的父节点
TreeNode pre = null;
while(cur != null){
if(cur.val == key){
break;
}
pre = cur;
if(cur.val > key){
cur = cur.left;
}
else{
cur = cur.right;
}
}
// 如果只有一个根节点
if(pre == null){
return deleteOneNode(cur);
}
// 要删除的 key 在左孩子
if(pre.left != null && pre.left.val == key){
pre.left = deleteOneNode(cur);
}
// 要删除的 key 在右孩子
if(pre.right != null && pre.right.val == key){
pre.right = deleteOneNode(cur);
}
return root;
}
}
同样本题解时间复杂度为 O(n) ,因为非递归法只额外开辟了常数级的空间,所以空间复杂度为 O(1) 。
图解删除二叉搜索树中的节点到这就结束啦!至此,二叉搜索树的【查找】、【插入】和【删除】等 3 大操作我都依次带着大家实战完了!
好累好累好累呀,快把夸我打在评论区!!!
好了,夸完就赶紧圆润的去刷题吧!
我是帅蛋,我们下次见~
