使用SPSS(27版本)以及ArcGIS软件做的一些计量地理学实验步骤记录与简略分析。主要有如下一些实验:地理数据的统计处理、相关分析、主成分分析、多元线性回归分析、聚类分析、时间序列数据分析、因子分析、地统计分析、趋势面分析、马尔可夫分析。
目录
实验一 地理数据的统计处理
一、实验目的:了解地理数据分布的基本特征,掌握地理数据分布特征的主要表征值。
二、实验内容:运用SPSS应用软件中的相关的模块,实验表1中的数据,进行地理数据的统计处理,重点掌握标准差、最大值、最小值、方差、算术平均数、众数、中位数、算数和以及偏态、峰度的计算,绘制统计柱状图等。
表1 某地区1992-2004年的农业总产值(亿元)
| 年份 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 |
| 农业产值 | 108 | 109 | 115 | 121 | 127 | 135 | 133 | 141 | 151 | 153 | 167 | 170 | 176 |
三、实验步骤与结果分析:
1、定义变量。打开SPSS数据编辑器,切换到变量视图,进行定义变量。
图1-1切换变量视图

图1-2定义变量名称与类型
2、数据录入。再切换到数据视图进行数据的录入。
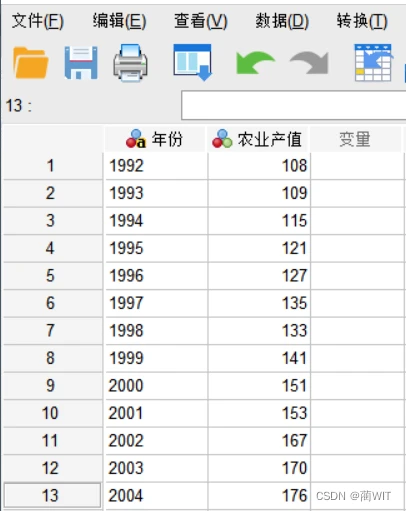
图1-3数据的录入
3、进行统计分析。打开“分析”→“描述性分析”→“频率”,
图1-4统计频率操作
图1-5设置要统计的类型
图1-6统计变量的设置
4、查看统计的结果。点击“确定”后,会自动生成Statistics 查看器窗口,在此可以查看统计的结果。
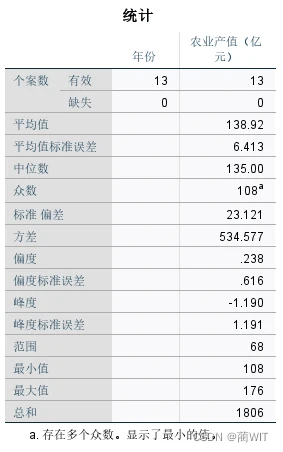
图1-7统计数据结果表
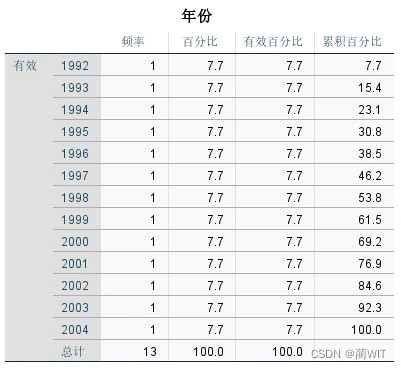
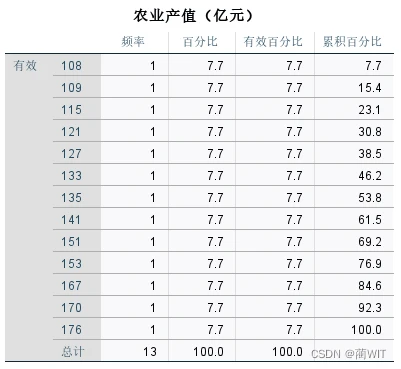
图1-8频率表
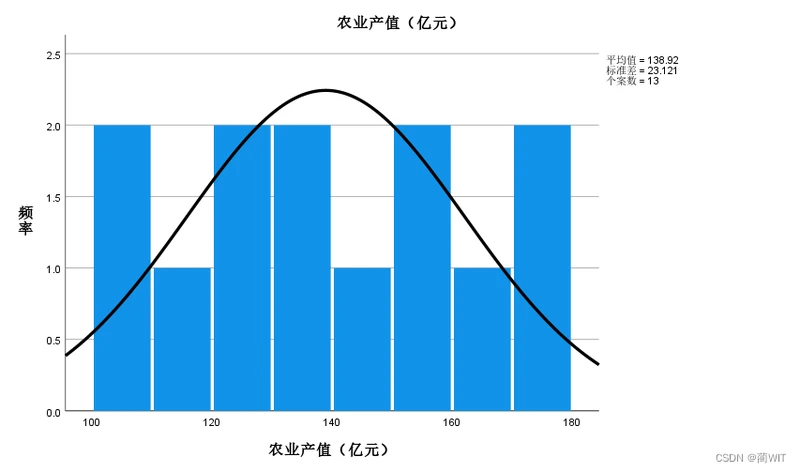
图1-9频率分布直方图
5、绘制数据的条形图,可以直观看出逐年份的农业产值增长情况,点击“图形”→“图表构建器”,可进行构建图表的选择与相关设置。
图1-10打开图表构建器
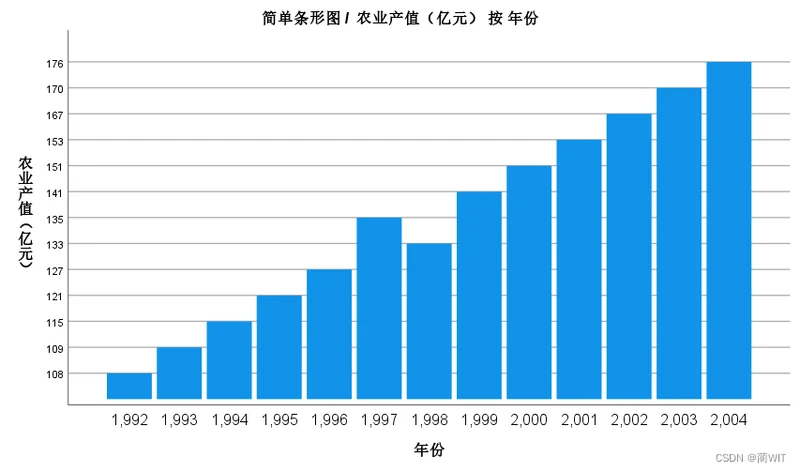
图1-11各年份农业产值柱状图
实验二 相关分析
一、实验目的:掌握相关分析、回归分析的定义、内涵,重点掌握一般相关系数的计算公式、利用所给数据能够建立一元线性与非线性回归方程,并能够进行检验。
二、实验内容:运用SPSS应用软件中的Correlate模块,利用表2中的数据,针对水土流失面积与土壤氮含量进行相关分析,进行两两要素间的相关分析,并能够进行检验;运用SPSS应用软件中的Regression模块建立一元线性和非线性方程,并进行检验,利用所给数据进行预测。
表2 某区域水土流失面积与土壤氮含量数据
| 序号 | 水土流失面积 | 土壤含氮量 | 序号 | 水土流失面积 | 土壤含氮量 |
| 1 | 0.8 | 6.6 | 7 | 5.6 | 2.4 |
| 2 | 1.4 | 5.2 | 8 | 6.5 | 2.3 |
| 3 | 2.0 | 4.8 | 9 | 7.1 | 2.1 |
| 4 | 2.7 | 3.9 | 10 | 7.7 | 2.3 |
| 5 | 3.3 | 3.7 | 11 | 8.3 | 1.7 |
| 6 | 4.1 | 3.2 | 12 | 9.2 | 1.5 |
三、实验步骤与结果分析:
1、定义变量与数据录入。打开SPSS数据编辑器,在变量视图定义变量,在数据视图录入数据。
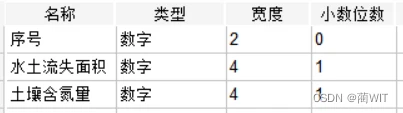
图2-1定义变量
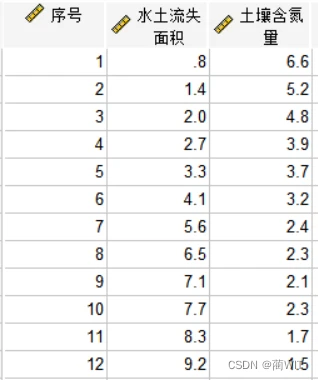
图2-2录入数据
2、散点图与线性趋势判定。作散点图,进行线性趋势判定。在SPSS 中打开图形构建器,制作散点图。
图2-3图形构建器
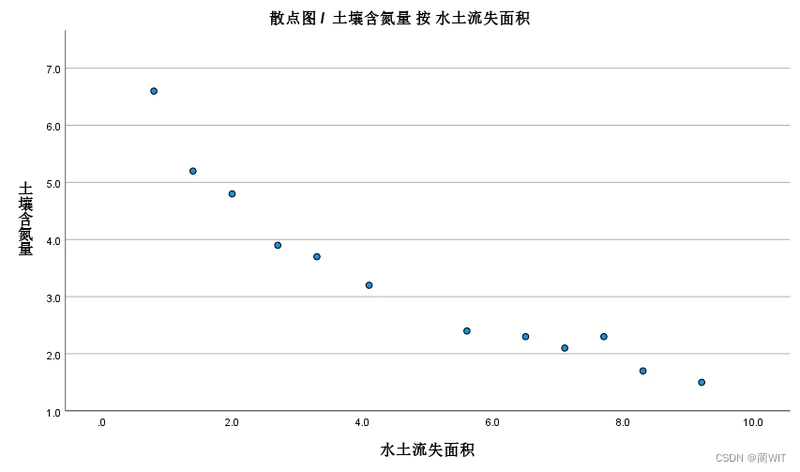
图2-4散点图
3、计算简单相关系数。点击“分析”→“相关”→“双变量”,展开双变量相关性分析对话框。
图2-5打开相关分析对话框操作
- 在变量栏中选中所要求的变量,将选择的变量移到“变量”矩形框中;从主对话框中选择“相关系数”的方法,系统默认的是Pearson,即皮尔逊相关(常用的一种方法)。显著性检验系统默认的是Tow-tailed,即双尾T检验,表示相关系数为0的假设检验成立的概率。如果是先不知道相关方向时选用Tow-tailed;如果事先知道方向时,选用One-tailed。
图2-6双变量相关性对话框
- “**”表示相关系数的显著性概率水平为0.01。“*”表示显著性水平为0.05。从图2-7中我们可以得到相关系数为-0.946,通过查看教材88页表格我们能够知道当a=0.01,f=12-2=10时,对应的值为0.7079,而0.946>0.7079,所以通过了相关检验。
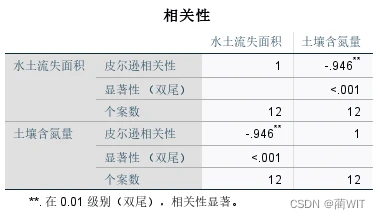
图2-7相关分析结果
4、计算偏相关系数。点击“分析”→“相关”→“偏相关”,展开偏相关性分析对话框。
图2-8打开偏相关分析对话框操作
- 在变量栏中选中进行偏相关分析的变量,移到“变量”矩形框中,把不参与偏相关分析的变量,移到“控制”矩形框中。显著性检验系统默认的是Tow-tailed,即双尾T检验,表示相关系数为0的假设检验成立的概率。如果是先不知道相关方向时选用Tow-tailed;如果事先知道方向时,选用One-tailed。
图2-9偏相关性对话框
- “**”表示相关系数的显著性概率水平为0.01。“*”表示显著性水平为0.05。在自由度为12-2-1=9时,查t分布表,t在置信水平之下,偏相关系数0.077是不显著的。
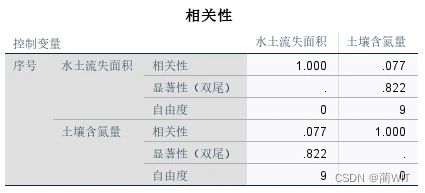
图2-10偏相关分析结果
5、建立一元线性模型。由上述散点图和相关分析结果,可知数据具有趋势性,可对其进行一元线性回归拟合。选择“分析”→“回归”→“线性”,打开“线性回归”对话框。
图2-11打开线性回归分析操作
- 在左侧的源变量中,选择一个变量进入“因变量”框中作为因变量,选择一个变量进入“自变量”框中,作自变量。自变量和因变量必须是数值型变量。在“方法”框中选择一种回归分析方法enter选项,步进法,即所选择的变量全部进入回归方程中。该选项是默认方式。
图2-12线性回归对话框
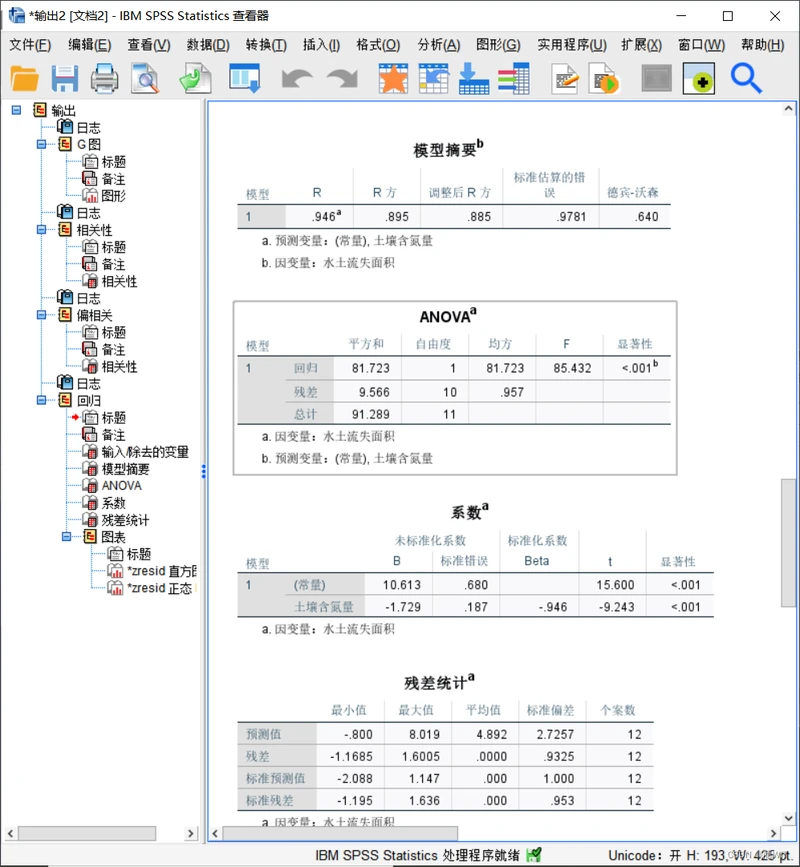
图2-13线性回归分析结果报告
6、结果解读与检验分析。
- 回归系数。如图2-14,可以读出回归系数:截距a=10.613,斜率b=0.680。
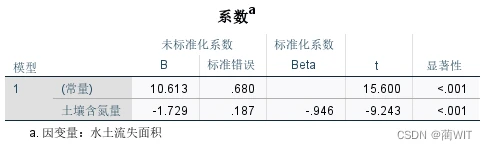
图2-14回归系数
- 拟合优度检验。如图2-15,可以读出相关系数R=0.946,测定系数R²=0.895。
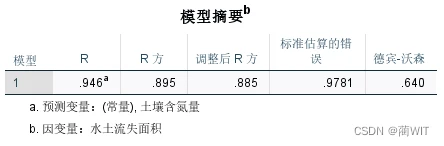
图2-15模型摘要
- F-检验。在ANOVA(方差分析Analysis of Variance 的缩写)中可以读到F-值:F=85.432。
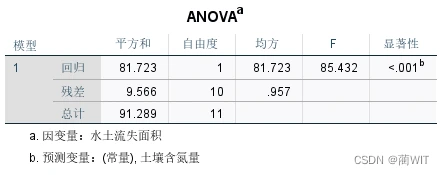
图2-16方差分析结果
- 标准误差检验。在模型摘要中可以读出标准离差(误差)s=0.9781.在残差统计表中可以给出了因变量y的均值:y_=4.892,两者相除可得变异系数ơ=0.1999。
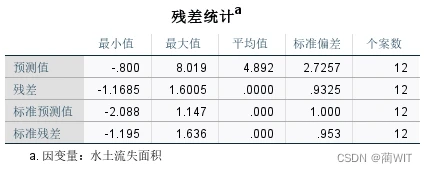
图2-17残差统计
- 在Output 中可以观察残差分布的正态概率图(应该呈现正态分布特征,图2-18)及其累计图(应该形成对角直线,图2-19)。残差分布概率越是具有正态分布即钟形曲线(bell-like curve)特征,表明残差分布越是随机,回归结果越是可靠。残差分布的累计概率越是接近对角线,表明残差分布越是随机,回归结果越可靠。
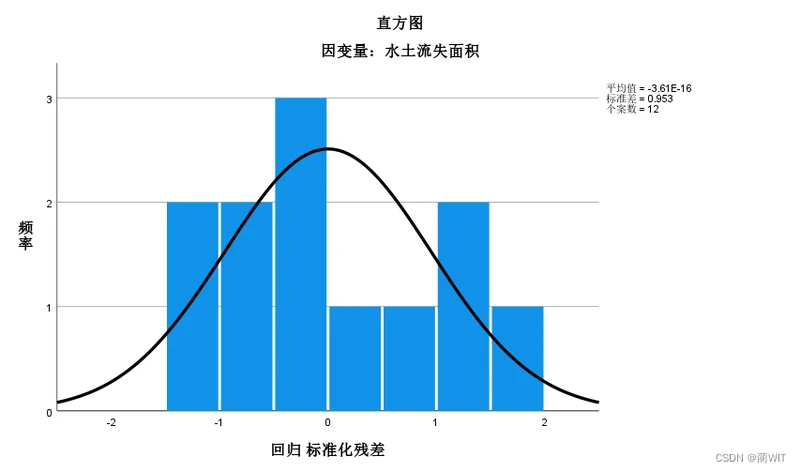
图2-18回归的标准残差频率分布直方图
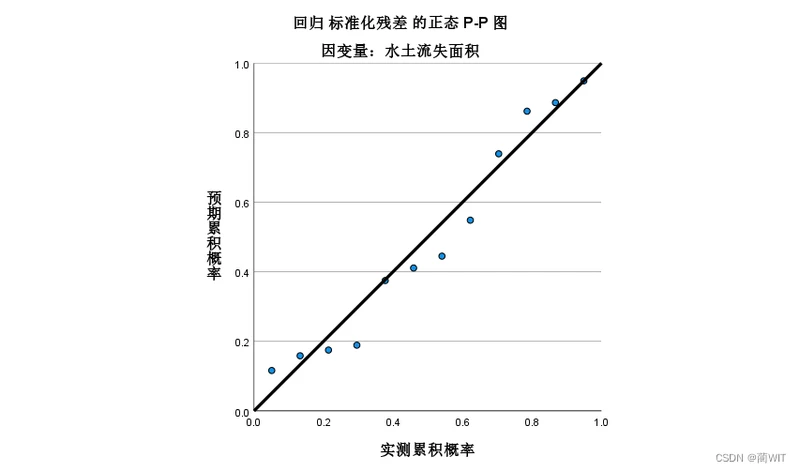
图2-19残差的累计概率图
实验三 主成分分析
一、实验目的:掌握主成分分析的定义、内涵,重点掌握一般主成分分成的计算步骤、利用所给数据能够建立主成分分析思路与结果,并能够进行检验。
二、实验内容:运用SPSS应用软件中的相关的模块,利用表3中的数据,针对中国主要城市影响经济发展的主要指标进行主成分分析。
表3 中国主要城市影响经济发展的主要指标
| 城 市 | 总人口 (万人) | 非农业 人口比(%) | 农 业总产值(万元) | 工 业 总产值(万元) | 客 运总 量(万人) | 货 运总 量(万吨) | 地方财政预算内收入(万元) | 城乡居民年底储蓄余额 (万元) | 在岗职工人数(万人) | 在岗职工工资总额(万元) |
| 北 京 | 1249.9 | 0.5978 | 1843427 | 19999706 | 20323 | 45562 | 2790863 | 26806646 | 410.8 | 5773301 |
| 天 津 | 910.17 | 0.5809 | 1501136 | 22645502 | 3259 | 26317 | 1128073 | 11301931 | 202.68 | 2254343 |
| 石 家 庄 | 875.4 | 0.2332 | 2918680 | 6885768 | 2929 | 1911 | 352348 | 7095875 | 95.6 | 758877 |
| 太 原 | 299.92 | 0.6563 | 236038 | 2737750 | 1937 | 11895 | 203277 | 3943100 | 88.65 | 654023 |
| 呼和浩特 | 207.78 | 0.4412 | 365343 | 816452 | 2351 | 2623 | 105783 | 1396588 | 42.11 | 309337 |
| 沈 阳 | 677.08 | 0.6299 | 1295418 | 5826733 | 7782 | 15412 | 567919 | 9016998 | 135.45 | 1152811 |
| 大 连 | 545.31 | 0.4946 | 1879739 | 8426385 | 10780 | 19187 | 709227 | 7556796 | 94.15 | 965922 |
| 长 春 | 691.23 | 0.4068 | 1853210 | 5966343 | 4810 | 9532 | 357096 | 4803744 | 102.63 | 884447 |
| 哈 尔 滨 | 927.09 | 0.4627 | 2663855 | 4186123 | 6720 | 7520 | 481443 | 6450020 | 172.79 | 1309151 |
| 上 海 | 1313.12 | 0.7384 | 2069019 | 54529098 | 6406 | 44485 | 4318500 | 25971200 | 336.84 | 5605445 |
| 南 京 | 537.44 | 0.5341 | 989199 | 13072737 | 14269 | 11193 | 664299 | 5680472 | 113.81 | 1357861 |
| 杭 州 | 616.05 | 0.3556 | 1414737 | 12000796 | 17883 | 11684 | 449593 | 7425967 | 96.9 | 1180947 |
| 宁 波 | 538.41 | 0.2547 | 1428235 | 10622866 | 22215 | 10298 | 501723 | 5246350 | 62.15 | 824034 |
| 合 肥 | 429.95 | 0.3184 | 628764 | 2514125 | 4893 | 1517 | 233628 | 1622931 | 47.27 | 369577 |
| 福 州 | 583.13 | 0.2733 | 2152288 | 6555351 | 8851 | 7190 | 467524 | 5030220 | 69.59 | 680607 |
| 厦 门 | 128.99 | 0.4865 | 333374 | 5751124 | 3728 | 2570 | 418758 | 2108331 | 46.93 | 657484 |
| 南 昌 | 424.2 | 0.3988 | 688289 | 2305881 | 3674 | 3189 | 167714 | 2640460 | 62.08 | 479555 |
| 济 南 | 557.63 | 0.4085 | 1486302 | 6285882 | 5915 | 11775 | 460690 | 4126970 | 83.31 | 756696 |
| 青 岛 | 702.97 | 0.3693 | 2382320 | 11492036 | 13408 | 17038 | 658435 | 4978045 | 103.52 | 961704 |
| 郑 州 | 615.36 | 0.3424 | 677425 | 5287601 | 10433 | 6768 | 387252 | 5135338 | 84.66 | 696848 |
| 武 汉 | 740.2 | 0.5869 | 1211291 | 7506085 | 9793 | 15442 | 604658 | 5748055 | 149.2 | 1314766 |
| 长 沙 | 582.47 | 0.3107 | 1146367 | 3098179 | 8706 | 5718 | 323660 | 3461244 | 69.57 | 596986 |
| 广 州 | 685 | 0.6214 | 1600738 | 23348139 | 22007 | 23854 | 1761499 | 20401811 | 182.81 | 3047594 |
| 深 圳 | 119.85 | 0.7931 | 299662 | 20368295 | 8754 | 4274 | 1847908 | 9519900 | 91.26 | 1890338 |
| 南 宁 | 285.87 | 0.4064 | 720486 | 1149691 | 5130 | 3293 | 149700 | 2190918 | 45.09 | 371809 |
| 海 口 | 54.38 | 0.8354 | 44815 | 717461 | 5345 | 2356 | 115174 | 1626800 | 19.01 | 198138 |
| 重 庆 | 3072.34 | 0.2067 | 4168780 | 8585525 | 52441 | 25124 | 898912 | 9090969 | 223.73 | 1606804 |
| 成 都 | 1003.56 | 0.335 | 1935590 | 5894289 | 40140 | 19632 | 561189 | 7479684 | 132.89 | 1200671 |
| 贵 阳 | 321.5 | 0.4557 | 362061 | 2247934 | 15703 | 4143 | 197908 | 1787748 | 55.28 | 419681 |
| 昆 明 | 473.39 | 0.3865 | 793356 | 3605729 | 5604 | 12042 | 524216 | 4127900 | 88.11 | 842321 |
| 西 安 | 674.5 | 0.4094 | 739905 | 3665942 | 10311 | 9766 | 408896 | 5863980 | 114.01 | 885169 |
| 兰 州 | 287.59 | 0.5445 | 259444 | 2940884 | 1832 | 4749 | 169540 | 2641568 | 65.83 | 550890 |
| 西 宁 | 133.95 | 0.5227 | 65848 | 711310 | 1746 | 1469 | 49134 | 855051 | 27.21 | 219251 |
| 银 川 | 95.38 | 0.5709 | 171603 | 661226 | 2106 | 1193 | 74758 | 814103 | 23.72 | 178621 |
| 乌鲁木齐 | 158.92 | 0.8244 | 78513 | 1847241 | 2668 | 9041 | 254870 | 2365508 | 55.27 | 517622 |
三、实验步骤与结果分析:
1、数据导入。在SPSS数据编辑器中选择“打开文件”图标,从excel中将数据导入进SPSS中。
图3-1读取Excel文件
图3-2导入数据
2、主成分(因子)分析相关设置。选择“分析”→“降维”→“因子”,打开因子分析对话框,然后依次进行选项设置。
图3-3打开因子分析操作
图3-4因子分析对话框
- “描述”选项。选中“单变量描述”复选项,则输出结果中将会给出原始数据的抽样均值、方差和样品数目(这一栏结果可供检验参考);选中“初始解”复选项,则会给出主成分载荷的公因子方差(这一栏数据分析时有用)。;选中“系数”复选框,将会给出原始变量的简单相关系数矩阵(分析时可参考);选中“显著性水平”,将会给出每一个相关系数相对于相关系数为0 时的单尾假设检验的显著性水平;选中“决定因子”,将会给出相关系数矩阵的行列式,如果希望在Excel 中对某些计算过程进行了解,可选此项;选中“KMO和巴特利特球形度检验”,将会给出KMO 和球形Bartlett 检验统计量。

图3-5设置“描述”选项
- “提取”选项。因子提取方法主要有7 种,在“方法” 栏中可以看到,系统默认的提取方法是主成分。选中“相关性矩阵”,主成分分析基于数据的相关系数矩阵进行分析。
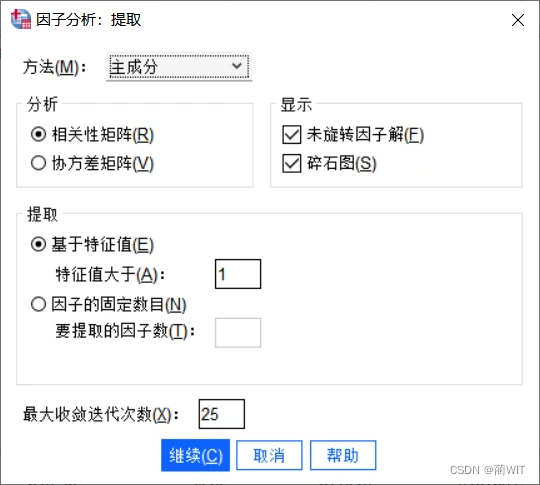
图3-6设置“提取”选项
- “因子得分”选项。选中“保存为变量”,分析结果中将会给出标准化的主成分得分(在数据表的后面),对主成分分析而言,三种方法没有分别,因此,采用系统默认的“回归”法即可。选中“显示因子得分系数矩阵,则在分析结果中给出因子得分系数矩阵和因子得分的相关系数矩阵(协方差矩阵)。
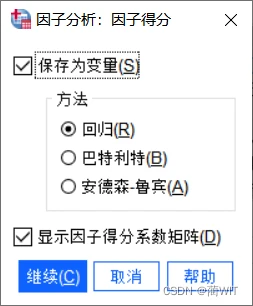
图3-7设置“因子得分”选项
- “选项”选项。对于数据没有缺失的情况下,或者对主成分载荷的排列方式没有特殊要求。Option 项可以不必理会。但是,当数据有缺失时,或者希望主成分载荷按某种规律排列,这一选项需要特别注意。
图3-8设置“选项”选项
- “旋转”选项。对于主成分分析来说,旋Rotation(转项)可以不必设置。不过有时候需要选中载荷图。
图3-9设置“旋转”选项
3、主成分分析结果解读。在分析结果中首先给出的是描述统计,即每个变量的平均值、标准偏差以及样品数量。
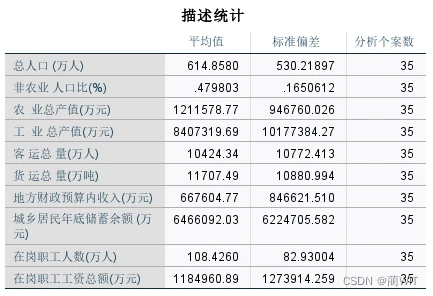
图3-10描述统计
- 相关性矩阵,即相关系数矩阵。一般而言,相关系数高的变量,大多会进入同一个主成分,但不尽然。相关系数矩阵给出的主要是简单相关系数,反映变量之间真实关系的则是偏相关系数。简单相关系数矩阵对主成分分析具有参考价值,毕竟主成分分析是从计算相关系数矩阵的特征根开始的。相关系数阵下面的是相关显著性水平矩阵。
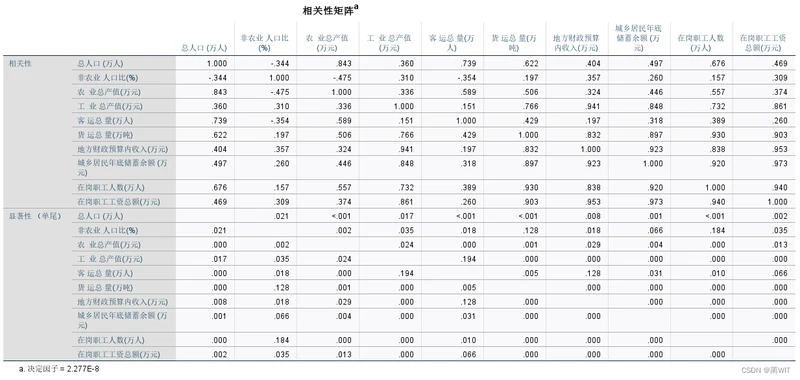
图3-11相关性矩阵
- 在KMO 和Bartlett 检验表中,给出了KMO 值以及用于Bartlett 检测的卡方近似值、自由度和显著性水平。如果KMO 值小于0.5时,那就不太适合开展主成分分析;KMO 值大于0.6 为“效果平庸”;KMO 值大于0.7 为“中度适宜”;KMO 值大于0.8 为“效果良好”。对于该例子,KMO=0.762,即中度适宜做主成分分析。计算的卡方值χ²=525.001,查表可知,在该概率值和自由度下,该值远大于临界值,Bartlett 检验可以通过。

图3-12 KMO和巴特利特检验
- 在公因子方差表中,给出了因子载荷阵的初始公因子方差(Initial)和提取公因子方差(Extraction)。提取提示的是,如果某个变量对应的提取公因子方差值太小,则要么去掉对应的变量,要么增加主成分的数目。可见公因子方差也是主成分提取数目的一个重要判据。
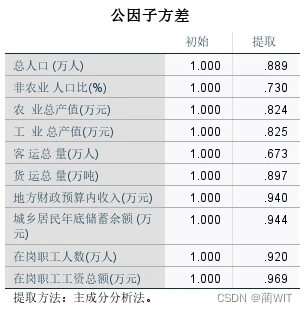
图3-13公因子方差
- 在总解释方差表的初始特征根中,给出了按顺序排列的主成分得分的方差,在数值上等于相关系数矩阵的各个特征根λ,因此可以直接根据特征根计算每一个主成分的方差百分比。依据全部特征根的总和等于变量数目,可以算出方差累计值。
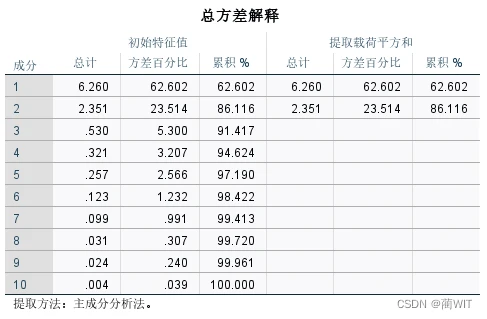
图3-14总方差解释
- 主成分的数目可以根据相关系数矩阵的特征根来判定。相关系数矩阵的特征根刚好等于主成分的方差,而方差是变量数据蕴涵信息的重要判据之一。根据λ值决定主成分数目的准则有三个方面:
- 只取λ>1 的特征根对应的主成分;(如图3-14,则取第1、2主成分)
- 累计百分比达到80%~85%以上的λ值对应的主成分;(如图3-15,则取第1、2主成分)
- 根据特征根变化的突变点决定主成分的数量。(如图3-16,则取第1、2主成分)
综上三个原则,可决定主成分的数目为2,即取第1、2主成分。
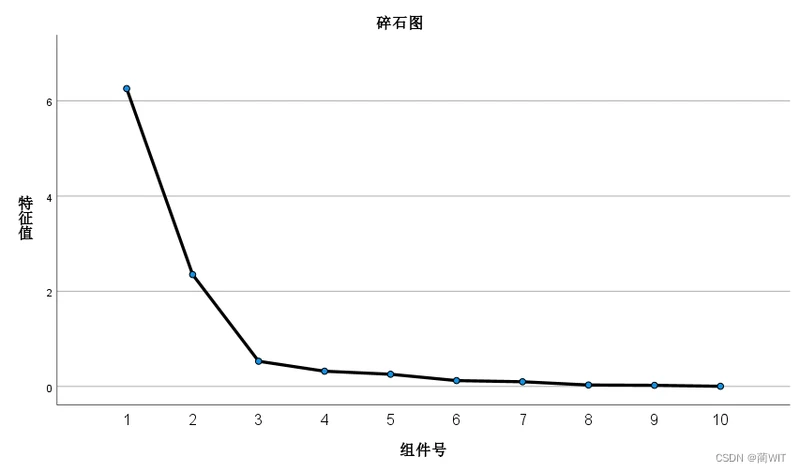
图3-15特征根数值衰减折线图(碎石图)
- 在成分矩阵中,给出了主成分载荷矩阵,每一列载荷值都显示了各个变量与有关主成分的相关系数(图3-16)。以第一列为例,0.690 实际上是总人口(万人)与第一个主成分的相关系数。
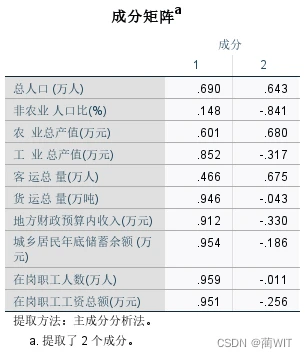
图3-16成分矩阵
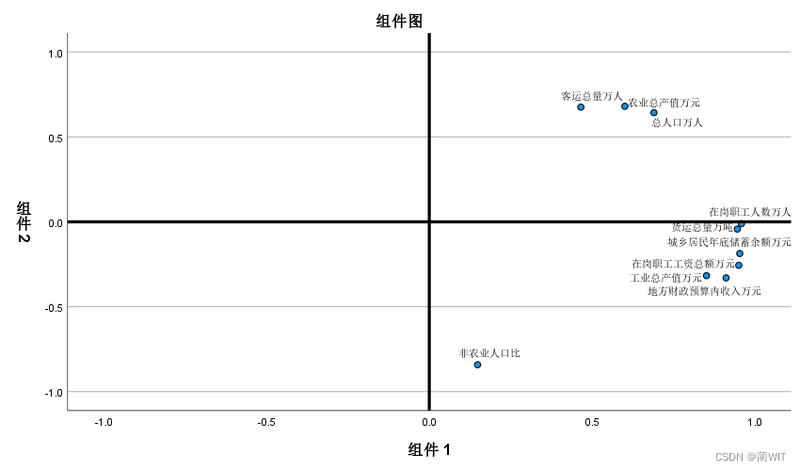
图3-17主成分荷载图(组件图)
- 成分得分系数矩阵,即主成分得分系数;成分得分协方差矩阵,主成分得分的协方差即相关系数。如图3-19,标准化主成分得分之间的协方差即相关系数为0(j≠k)或1(j=k),这意味着主成分之间彼此正交即垂直。
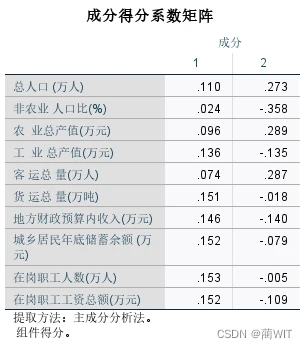
图3-18成分得分系数矩阵
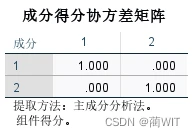
图3-19成分得分协方差矩阵
4、主成分分析。如图3-20所示,可以看出在岗职工人数、在岗职工工资总额以及城乡居民年底储蓄余额在第一主成分上载荷较大,亦即与第一主成分的相关系数较高;非农业人口比在第二主成分上的载荷绝对值较大,即负相关程度较高。因此可将主成分命名如下:
第一主成分:居民薪资-储蓄主成分。
第二主成分:第一产业(农业)人口比主成分。
利用主成分载荷矩阵可以对中国主要城市的发展情况进行初步分析。不仅如此,还可以根据主成分得分开展综合评价。事实上,将图3-20中的主成分得分即非标准化的因子得分加和,就可得到各个主要城市的综合得分。根据综合得分排序,就可以看出不同城市的影响经济发展的主要指标。
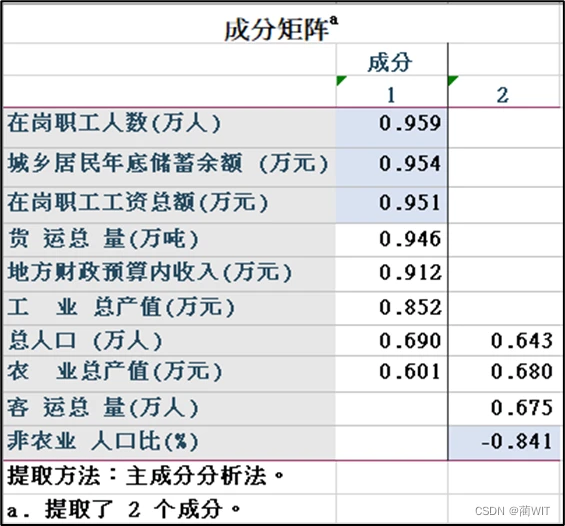
图3-20成分矩阵要素归类图
实验四 多元线性回归分析
一、实验目的:掌握多元线性回归分析的定义、内涵,重点掌握多元线性回归分析的计算步骤、利用所给数据能够建立多元线性回归分析思路与结果,并能够进行检验。
二、实验内容:运用SPSS应用软件中的相关的模块,利用表4中的数据,分析降水量和蒸发量对径流深的影响。
表4 河流径流深度及年降水量与蒸发量表
| 河流序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 年降水量 | 1150 | 1170 | 1154 | 1232 | 910 | 1676 | 1449 | 1850 | 1690 | 2000 | 1590 |
| 年蒸发量 | 496 | 604 | 610 | 707 | 546 | 740 | 718 | 752.6 | 722 | 518 | 816 |
| 径流深度 | 753 | 565 | 543.2 | 524.6 | 363.5 | 936 | 731 | 1097.1 | 967.5 | 1481 | 804 |
三、实验步骤与结果分析:
1、数据导入。打开SPSS数据编辑器,在变量视图定义变量,在数据视图录入数据。
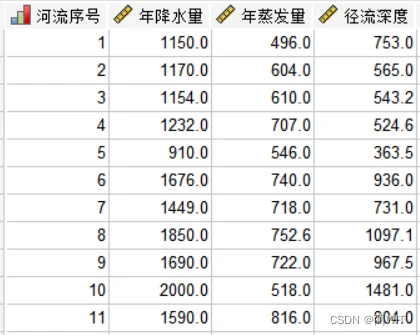
图4-1录入数据
2、回归操作。选择“分析”→“回归”→“线性”,打开“线性回归”对话框。在对话框中,采用输入(Enter)法,该方法纳入全部选中的变量。
图4-2打开线性回归分析操作
- 在“线性回归”对话框中,将“径流深度”置于因变量(Dependent)的空白栏,将“年蒸发量”和“年降水量”置于自变量(Independent(s))的空白栏。在统计(Statistics)选项框中选择“DW德宾-沃森”,还应该选择“部分相关性与偏相关性”以及“共线性诊断”。然后继续。在图形(Plots)选项框中,可以选择“直方图”和“正态概率图”以及“生成所有局部图”。
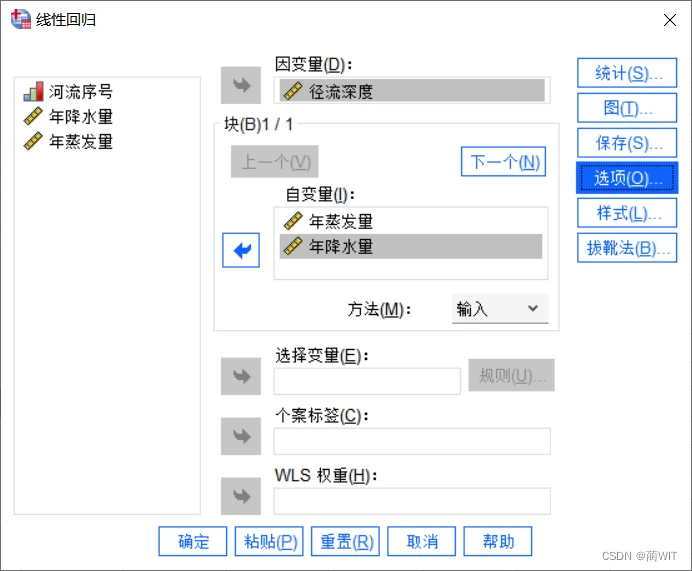
图4-3“线性回归”对话框
3、回归结果分析。点击“确定”即得到多元线性回归分析结果,首先给出的变量取舍表,给出的采用的变量、剔除的变量和回归方法,此表中没有剔除变量。

图4-4变量取舍表
- 在Model Summary(模型摘要)表中(图4-5),可以读到复相关系数R =0.996、测定系数R²=0.992、估计的标准误差s =31.8696以及DW值DW = 1.495(查表可知可以通过检验)。至于0.990为校正测定系数(adjusted R square)。
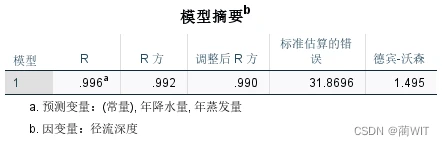
图4-5模型摘要表
- 在ANOVA(方差分析)表中(图4-6),可以读到回归平方和SSr = 984885.249,剩余平方和SSe=8135.351,总平方和SSt=993010.600,显然R²=SSr/SSt=0.992。同时,可以读到F=484.846。
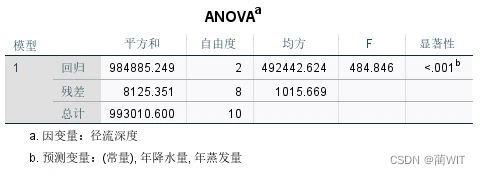
图4-6方差分析表
- 在系数(Coefficients)表中(图4-7),可以读到各个回归系数:a =81.010,b1=-1.083,b2=0.989,以及回归系数对应的误差,据此可以建立回归模型:Ў=81.010-1.083x1+0.989x2。同时可以读到各个回归系数对应的t值:截距ta=1.234,tb1=-10.567,tb2=31.089。通过“显著性值”(Sig.值)是否小于0.05可以直接判断t值是否可以通过检验。
- 在系数表的右半部分还可以读到零阶相关系数,实际上是各个自变量与因变量的简单相关系数,与之对应的是偏相关系数和部分相关系数。还有“共线性统计”,一个是Tol容差,单从数值上讲,容许度越接近1值越好,一是VIF方差膨胀因子,它在数值上为容许度的倒数,即有VIF=1/Tol,经验上,要求VIF值小于10。
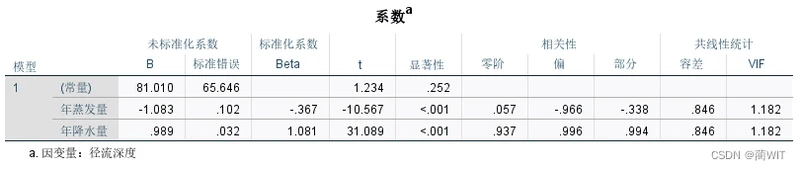
图4-7各种系数表
- 在共线性诊断表中,特征值提供了模型参数敏感度的一种判据,当特征值接近于0时,自变量之间的相关性程度较高,这时样本数据稍有变化,就会对回归系数影响很大。条件指标(病态指数)是最大特征值与最小特征值比值的平方根。当病态指数大于15 时,表明存在多重共线性;当病态指数大于30 时,表明共线性程度十分严重。方差比也是与特征根相联系的统计参量,当某两个以上的变量的方差比较大时,表明这些变量之间存在多重共线性问题。
- 从共线性诊断表中可以看到(图4-8):当Dimension(维)≥2时,特征值(EV)趋近于0,因此,对于本例,要想完全消除共线性,至多可以引进一个自变量。条件指标中,当Dimension(维)≥3时,值大于15,存在多重共线性。
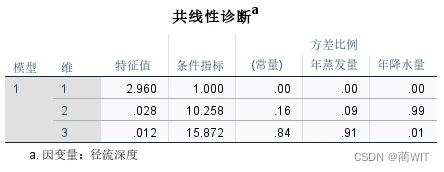
图4-8多重共线性诊断表
- 在残差统计表中可以读到因变量的平均值796.9,结合前面的估计标准误差s=31.8696,可得误差检验系数δ= 31.8696/796.9=0.039992。
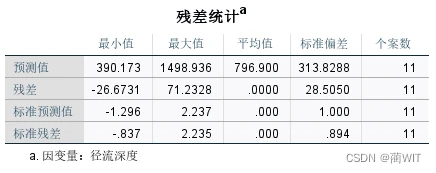
图4-8残差统计表
- 回归标准残差的直方图(图4-9)应该呈正态分布,而下图不具备正态曲线的钟形图式:bell-shaped curve。
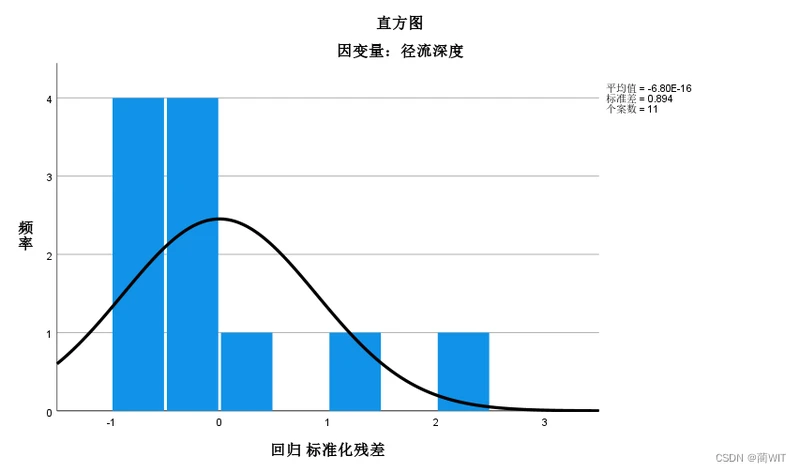
图4-9回归标准残差的直方图
- 在累计概率分布图中,累计概率点列应该沿着对角线分布(图4-10),当且仅当观察的累计概率与预期的累计概率相等时才会形成严格意义的对角线,统计结果给出的坐标图越接近对角线说明回归效果越好(下图的分布有些偏离对角线较远)。
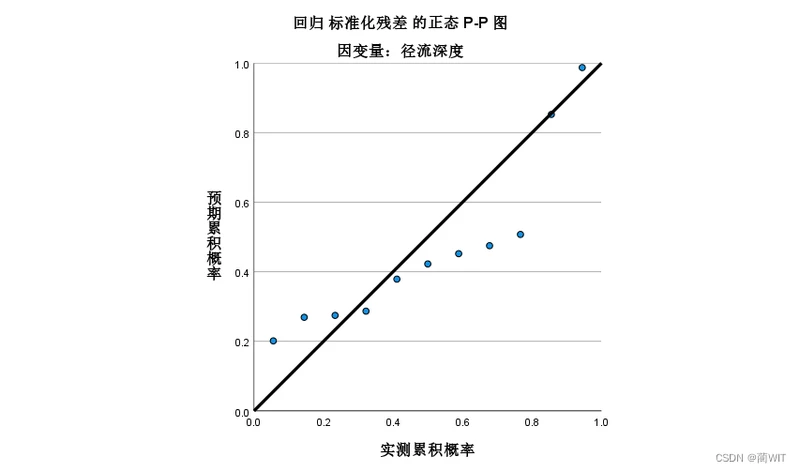
图4-10累计概率分布图
- 自变量与因变量残差的散点图(图4-11和图4-13),以没有任何明确的趋势为佳,即理当为完全随机的点列(下面两个散点图有些具有某种趋势,尤其是散点图二,趋势性较明显)。
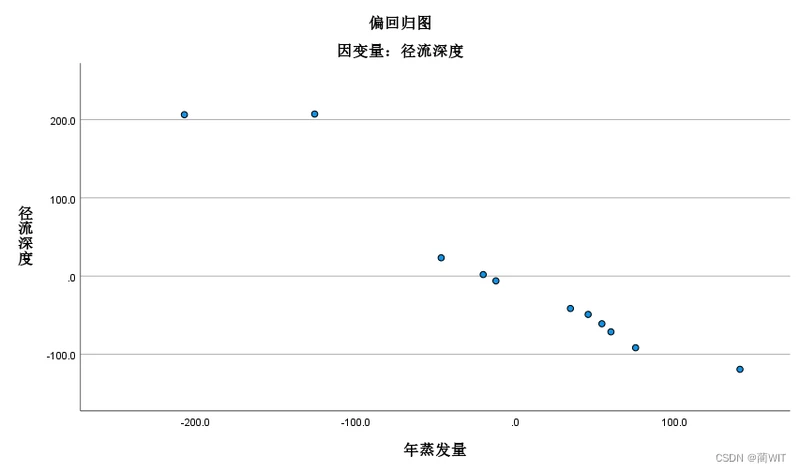
图4-11散点图一
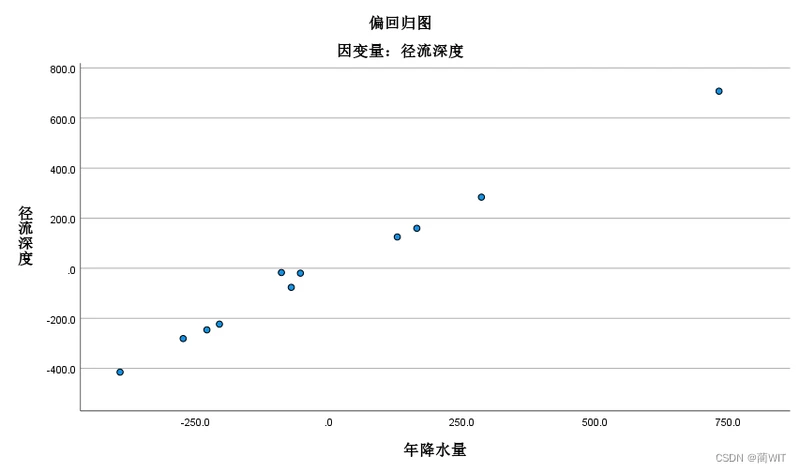
图4-12散点图二
实验五 聚类分析
一、实验目的:掌握聚类分析的定义、内涵,重点掌握聚类分析的计算步骤、利用所给数据能够建立聚类分析思路与结果,并能够进行检验。
二、实验内容:运用SPSS应用软件中的相关的模块,利用表5中的数据,对 21个农业区的各项指标数据进行聚类分析。
表5 20个农业区的各项指标数据
| 样本序号 | 人口密度 | 人均耕地面积 | 森林覆盖率 | 农民人均纯收入 | 人均粮食产量 | 经济作物占农作物播面比例 | 耕地占土地面积比率 | 果园与林地面积之比 | 灌溉田占耕地面积之比 |
| 1 | 363.912 | 0.352 | 16.1 | 192.11 | 295.34 | 26.724 | 18.492 | 2.231 | 26.262 |
| 2 | 141.503 | 1.684 | 24.3 | 1752.35 | 452.26 | 32.314 | 14.464 | 1.455 | 27.066 |
| 3 | 100.695 | 1.067 | 65.6 | 1181.54 | 270.12 | 18.266 | 0.162 | 7.474 | 12.489 |
| 4 | 143.739 | 1.336 | 33.21 | 1436.12 | 354.26 | 17.486 | 11.805 | 1.892 | 17.534 |
| 5 | 131.412 | 1.623 | 16.61 | 1405.09 | 586.59 | 40.683 | 14.401 | 0.303 | 22.932 |
| 6 | 68.337 | 2.032 | 76.2 | 1540.29 | 216.39 | 8.128 | 4.065 | 0.011 | 4.861 |
| 7 | 95.416 | 0.801 | 71.11 | 926.35 | 291.52 | 8.135 | 4.063 | 0.012 | 4.862 |
| 8 | 62.901 | 1.652 | 73.31 | 1501.24 | 225.25 | 18.352 | 2.645 | 0.034 | 3.201 |
| 9 | 86.624 | 0.841 | 68.9 | 897.36 | 196.37 | 16.861 | 5.176 | 0.055 | 6.167 |
| 10 | 91.394 | 0.812 | 66.5 | 911.24 | 226.51 | 18.279 | 5.643 | 0.076 | 4.477 |
| 11 | 76.912 | 0.858 | 50.3 | 103.52 | 217.09 | 19.793 | 4.881 | 0.001 | 6.165 |
| 12 | 51.274 | 1.041 | 64.61 | 968.33 | 181.38 | 4.005 | 4.066 | 0.015 | 5.402 |
| 13 | 68.831 | 0.836 | 62.8 | 957.14 | 194.04 | 9.11 | 4.484 | 0.002 | 5.79 |
| 14 | 77.301 | 0.623 | 60.1 | 824.37 | 188.09 | 19.409 | 5.721 | 5.055 | 8.413 |
| 15 | 76.948 | 1.022 | 68 | 1255.42 | 211.55 | 11.102 | 3.133 | 0.01 | 3.425 |
| 16 | 99.265 | 0.654 | 60.7 | 1251.03 | 220.91 | 4.383 | 4.615 | 0.011 | 5.593 |
| 17 | 118.505 | 0.661 | 63.3 | 1246.47 | 242.16 | 10.706 | 6.053 | 0.154 | 8.701 |
| 18 | 141.473 | 0.737 | 54.21 | 814.21 | 193.46 | 11.419 | 6.442 | 0.012 | 12.945 |
| 19 | 137.761 | 0.598 | 55.9 | 1124.05 | 228.44 | 9.521 | 7.881 | 0.069 | 12.654 |
| 20 | 117.612 | 1.245 | 54.5 | 805.67 | 175.23 | 18.106 | 5.789 | 0.048 | 8.461 |
| 21 | 122.781 | 0.731 | 49.1 | 1313.11 | 236.29 | 26.724 | 7.162 | 0.092 | 10.078 |
三、实验步骤与结果分析:
1、数据导入。在SPSS数据编辑器中选择“打开文件”图标,从excel中将数据导入进SPSS中。
图5-1读取Excel文件
图5-2导入数据
2、打开“聚类分析”对话框。选择“分析”→“分类”→“系统聚类”,打开系统聚类分析对话框。
图5-3打开系统聚类操作
图5-4“系统聚类分析”对话框
3、聚类分析选项设置。在源变量框中选中需要进行分析的变量,点击右边的箭头符号,将需要的变量调入变量栏内,在“聚类”选项中有Q 型(个案)和R 型(变量)两种类型,我们现在是对样品进行聚类,所以选择“个案”。选中显示图表。
- 对话框中其他选项卡可默认,在“方法”选项卡中,聚类方法选择最邻近元素(最短距离法),距离测度选择夹角余弦(Cosine),为消除变量量纲的影响,采用“Z得分法”对数据进行标准化处理。设置完成以后,单击“继续”按钮完成设置。
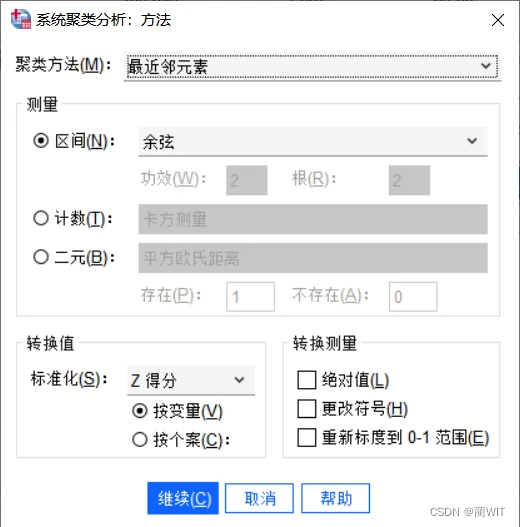
图5-5设置“方法”选项
4、聚类结果解读。在输出结果中,首先给出的是个案处理摘要。从摘要中可以看出:有效个案的数目和百分比,缺失个案的数目和百分比,全部个案的数目和百分比。由于没有数据缺失,故全部21个农业区个案参与聚类,有效个案为100%。
图5-6个案处理摘要
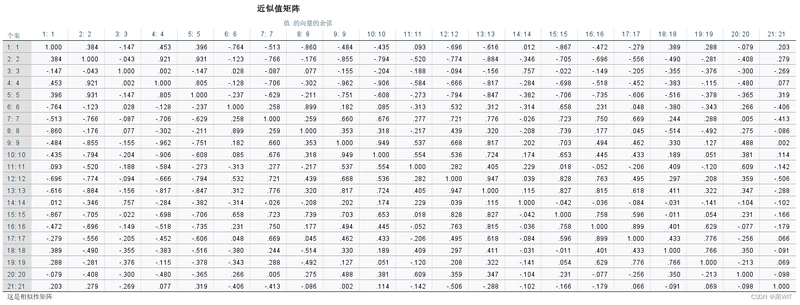
图5-7近似值矩阵
- 近似值矩阵是由夹角余弦代表的邻近性矩阵,实际上是一个相似系数矩阵。夹角余弦矩阵是广义的距离矩阵,是聚类分析的出发点。
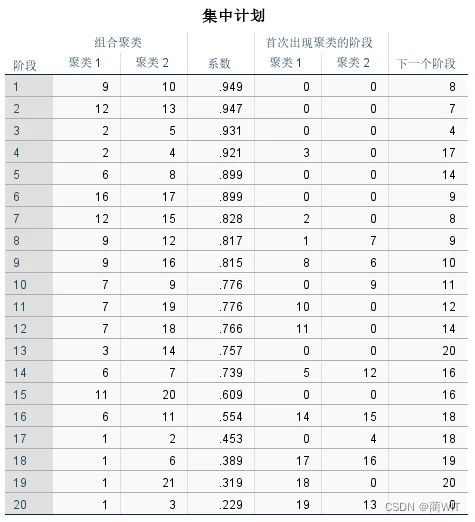
图5-8聚类进度表
- 聚类进度表可以与前面的近似值矩阵结合起来看。从进度表中可以看出,第1阶段,首先将第9号样品和第10号样品聚为一类,这两个样品的夹角余弦值最大,为0.949——检查近似值矩阵,发现两者的夹角余弦值为0.949,除对角线元素外,为最大数值。下一次要到第8阶段才会与这两个样品发生联系。以此来分析每一阶段。
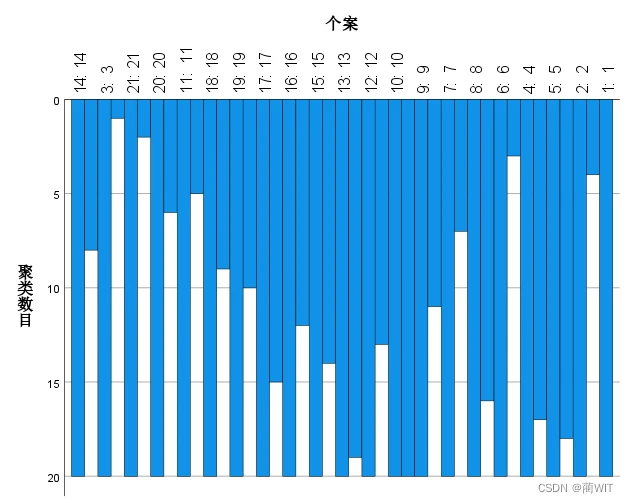
图5-9聚类结果冰柱图
- 冰柱图是聚类分析结果的表现形式之一,如图5-9,根据图中蓝色条带的长度,可以判断样品划分的归属。首先找寻最短的蓝色条带的位置,这个条带将全部对象分为两大类:左边为一类,右边为另一类,然后再寻找次短的位置,将这个位置将上述两个亚类再分为两类,分析方法依此类推。
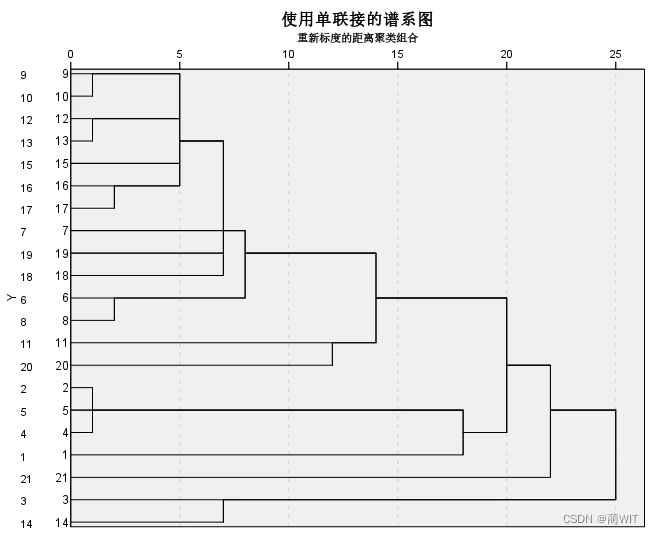
图5-10聚类分析的树形图
- 树形图是解读聚类分析结果最直观的方式,如图5-10。树形图的表示方法是,大尺度分出大类,小尺度分出细类。从图中易知:3号、14号属于一个亚类,其余的则属于另外一个亚类,依此类推。
实验六 时间序列数据分析
一、实验目的:掌握时间序列数据分析的定义、内涵,重点掌握时间序列数据分析的计算步骤、利用所给数据能够建立时间序列数据分析思路与结果,并能够进行检验。
二、实验内容:运用SPSS应用软件中的相关的模块,利用表6中的数据,采用ARIMA模型进行预测分析。
表6 时间序列数据分析数据
| 年份 | T(时间变量)=年份-1970 | y (人口,单位:人) |
| 2001 | 31 | 34510 |
| 2002 | 32 | 34510 |
| 2003 | 33 | 34511 |
| 2004 | 34 | 34512 |
| 2005 | 35 | 34513 |
| 2006 | 36 | 34514 |
| 2007 | 37 | 34514 |
| 2008 | 38 | 34515 |
| 2009 | 39 | 34516 |
| 2010 | 40 | 34516 |
三、实验步骤与结果分析:
1、数据导入。在SPSS数据编辑器中选择“打开文件”图标,从excel中将数据导入进SPSS中。

图6-1读取Excel文件
图6-2导入数据
2、时间序列分析预操作。先选择“数据”→“定义日期和时间”,进行时间变量的定义(数据中预先定义好可直接使用);选择“分析”→“时间序列预测”→“序列图”,获取序列图进行图像化观察;选择“分析”→“时间序列预测”→“自相关”,进行平稳性分析。
图6-3定义日期
图6-4获取序列图对话框
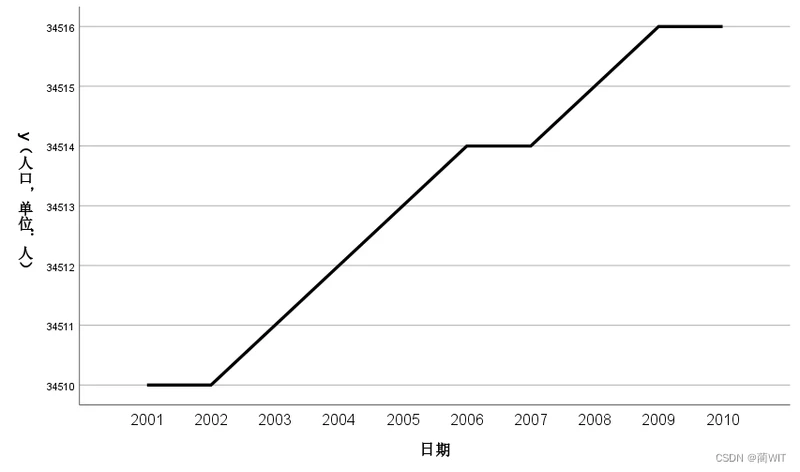
图6-5时间序列图
图6-6“自相关性”对话框(平稳性分析)
- 因为ARIMA模型要求序列是平稳序列,因此要对数据进行平稳性分析,得到其自相关图和偏相关图。如图6-6和图6-7,可以看出自相关图(ACF)和偏自相关图(偏ACF)大部分编号位于置信区间内部,说明序列是基本平稳的。
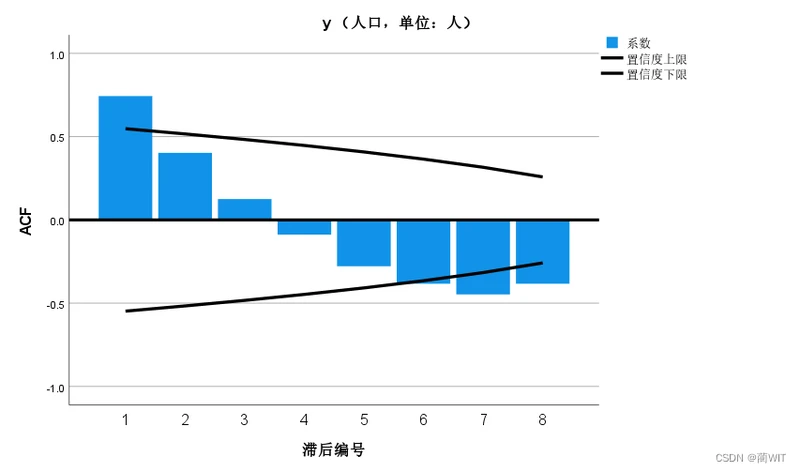
图6-7自相关图
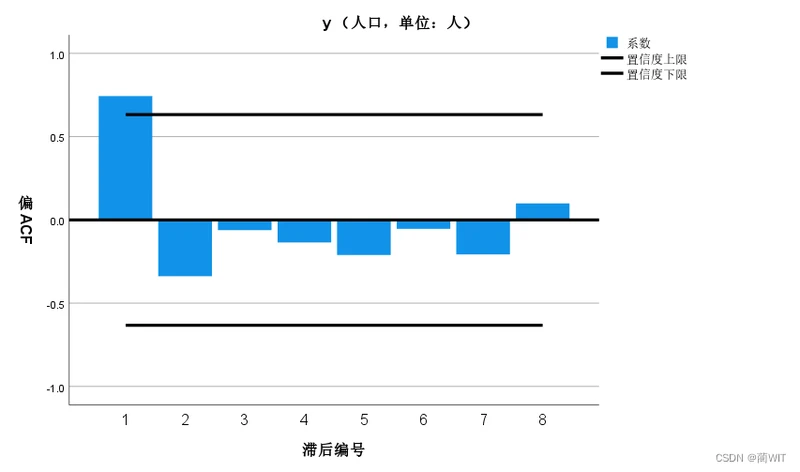
图6-8偏自相关图
3、设置时间序列建模器。选中“分析”→“时间序列预测”→“创建传统模型”,打开“时间序列建模器”对话框。进行时间序列分析的相关的选项设置。
图6-9打开“时间序列建模器”操作
- 在“时间序列建模器”中,因变量选择“人口数”,自变量选择“时间变量”,方法选择ARIMA,打开方法的“条件”选项卡,设置ARIMA条件:一般情况下差值(d)设为1,再根据前面的自相关图和偏自相关图,可知ACF有4阶截尾,所以自回归(p)设为4,偏ACF有一阶截尾,所以移动平均值(q)设为1。其他选项卡依据所需设置。
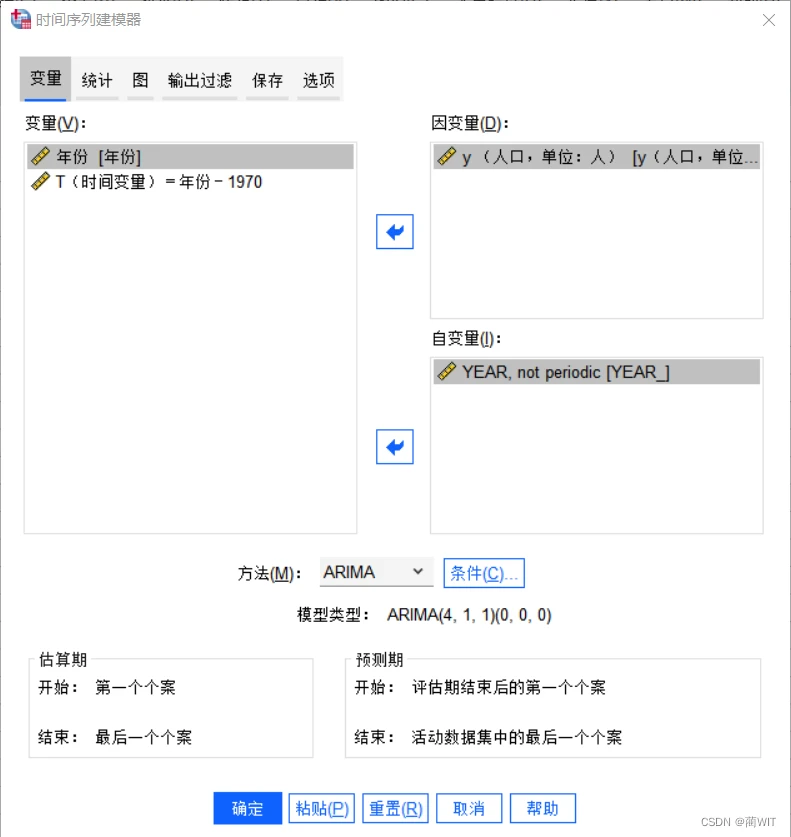
图6-10时间序列建模器设置
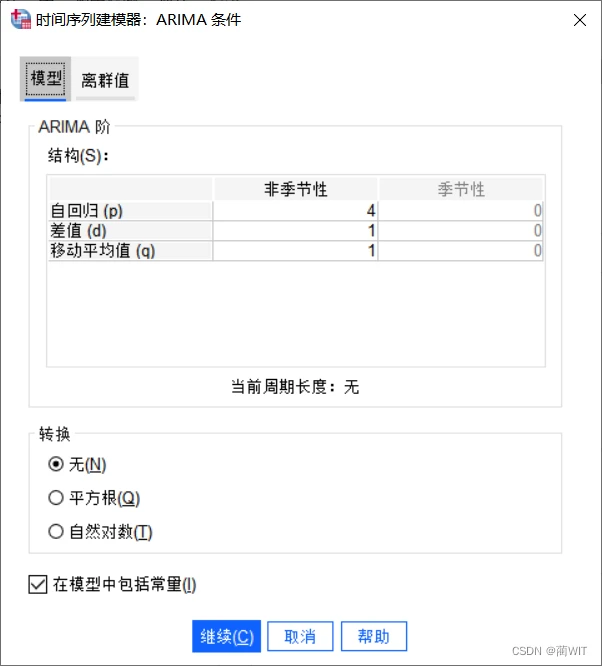
图6-11设置ARIMA的条件
4、时间序列分析结果解读。在时间序列建模器输出的分析结果中,首先给出的是模型描述,然后给出了模型摘要以及预测结果图表,另外,在数据视图里,还给出了具体的预测值。

图6-12模型描述
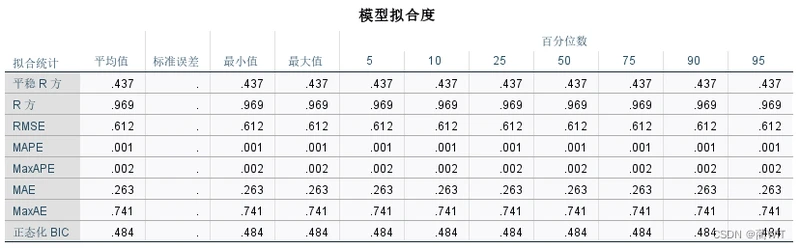
图6-13模型拟合度表
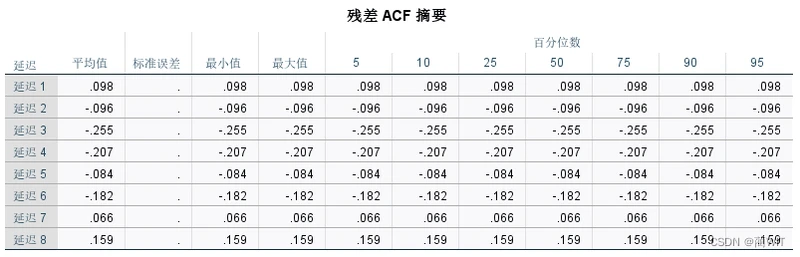
图6-14残差ACF摘要表
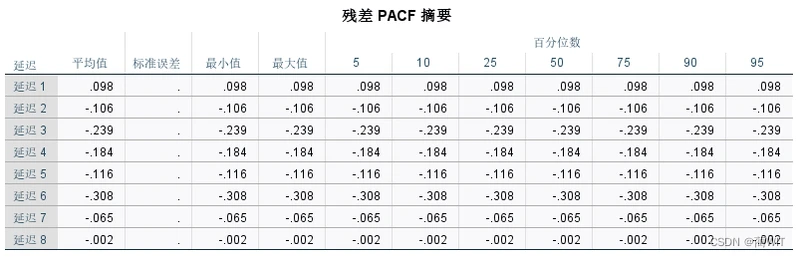
图6-15残差PACF摘要表

图6-16模型统计表
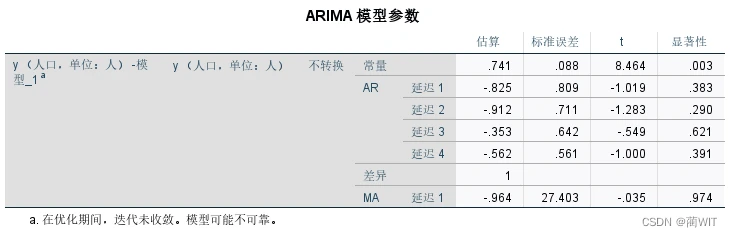
图6-17 ARIMA模型参数表

图6-18预测表
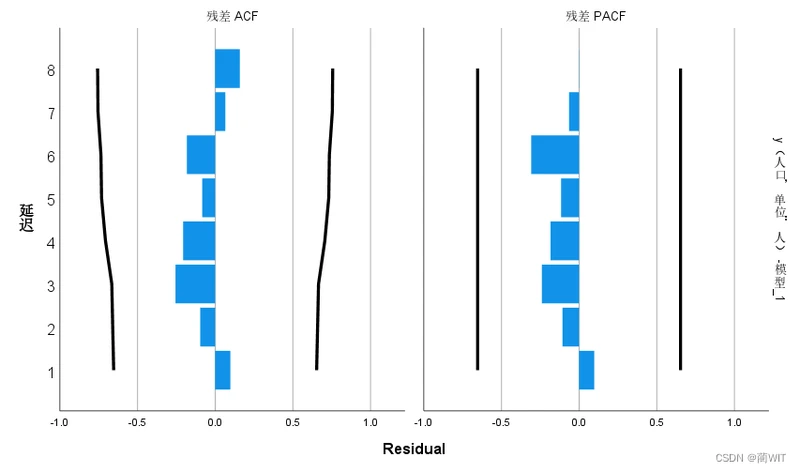
图6-19预测残差 ACF/PACF 图表
- 在时间序列图表中表示了该时间序列模型的原始数据图、模型拟合值、模型预测值,如图6-20。从图中可知,拟合序列趋势与真实序列趋势有极大的相似性,说明拟合效果较好。
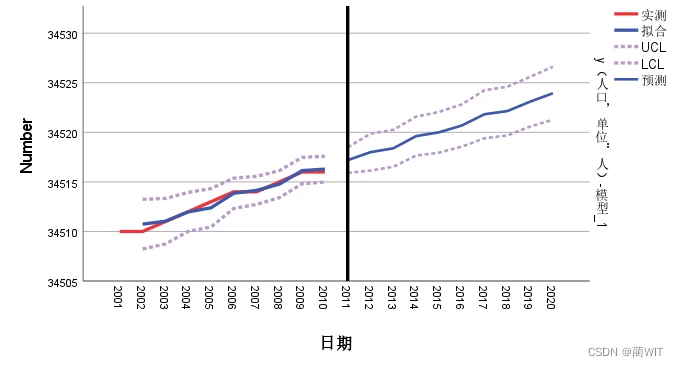
图6-20序列图表
实验七 因子分析
一、实验目的:掌握因子分析的定义、内涵,重点掌握因子分析的计算步骤、利用所给数据能够建立因子分析思路与结果,并能够进行检验。
二、实验内容:运用SPSS应用软件中的相关的模块,利用表7中的数据,为25名健康人的7项生化检验结果,7项系列化检验指标依次为X1至X7,对该资料进行因子分析。
表7 25名健康人的7项生化检验结果
| X1 | X2 | X3 | X4 | X5 | X6 | X7 |
| 3.76 | 3.66 | 0.54 | 5.28 | 9.77 | 13.74 | 4.78 |
| 8.59 | 4.99 | 1.34 | 10.02 | 7.5 | 10.16 | 2.13 |
| 6.22 | 6.14 | 4.52 | 9.84 | 2.17 | 2.73 | 1.09 |
| 7.57 | 7.28 | 7.07 | 12.66 | 1.79 | 2.10 | 0.82 |
| 9.03 | 7.08 | 2.59 | 11.76 | 4.54 | 6.22 | 1.28 |
| 5.51 | 3.98 | 1.3 | 6.92 | 5.33 | 7.3 | 2.4 |
| 3.27 | 0.62 | 0.44 | 3.36 | 7.63 | 8.84 | 8.39 |
| 8.74 | 7 | 3.31 | 11.68 | 3.53 | 4.76 | 1.12 |
| 9.64 | 9.49 | 1.03 | 13.57 | 13.13 | 18.52 | 2.35 |
| 9.73 | 1.33 | 1 | 9.87 | 9.87 | 11.06 | 3.7 |
| 8.59 | 2.98 | 1.17 | 9.17 | 7.85 | 9.91 | 2.62 |
| 7.12 | 5.49 | 3.68 | 9.72 | 2.64 | 3.43 | 1.19 |
| 4.69 | 3.01 | 2.17 | 5.98 | 2.76 | 3.55 | 2.01 |
| 5.51 | 1.34 | 1.27 | 5.81 | 4.57 | 5.38 | 3.43 |
| 1.66 | 1.61 | 1.57 | 2.8 | 1.78 | 2.09 | 3.72 |
| 5.90 | 5.76 | 1.55 | 8.84 | 5.4 | 7.50 | 1.97 |
| 9.84 | 9.27 | 1.51 | 13.6 | 9.02 | 12.67 | 1.75 |
| 8.39 | 4.92 | 2.54 | 10.05 | 3.96 | 5.24 | 1.43 |
| 4.94 | 4.38 | 1.03 | 6.68 | 6.49 | 9.06 | 2.81 |
| 7.23 | 2.3 | 1.77 | 7.79 | 4.39 | 5.37 | 2.27 |
| 9.46 | 7.31 | 1.04 | 12 | 11.58 | 16.18 | 2.42 |
| 9.55 | 5.35 | 4.25 | 11.74 | 2.77 | 3.51 | 1.05 |
| 4.94 | 4.52 | 4.5 | 8.07 | 1.79 | 2.1 | 1.29 |
| 8.21 | 3.08 | 2.42 | 9.1 | 3.75 | 4.66 | 1.72 |
| 9.41 | 6.44 | 5.11 | 12.5 | 2.45 | 3.1 | 0.91 |
三、实验步骤与结果分析:
1、数据导入。在SPSS数据编辑器中选择“打开文件”图标,从excel中将数据导入进SPSS中。
图7-1读取Excel文件
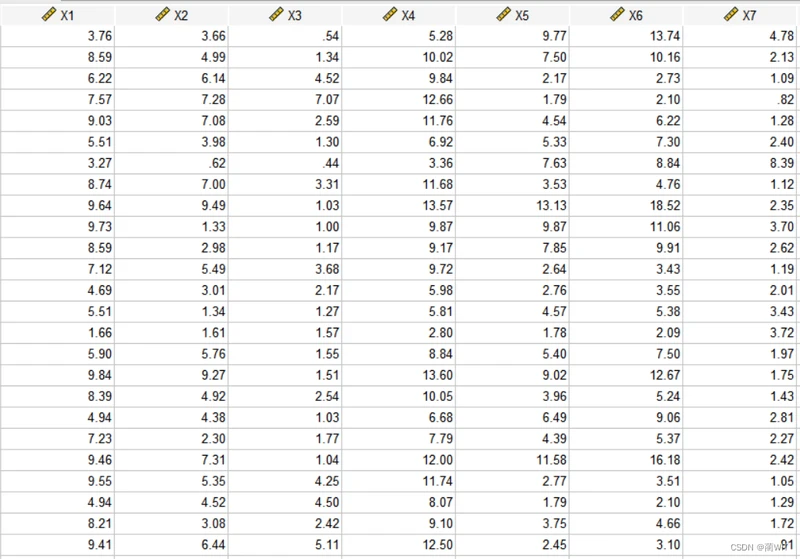
图7-2导入数据
2、因子分析相关设置。选择“分析”→“降维”→“因子”,打开因子分析对话框,然后依次进行选项设置。
图7-3因子分析对话框
- “描述”、“提取”等选项卡可以参考主成分分析中的设置,主要在于“旋转”选项卡的设置。在Method(方法)栏中选中Varimax(最大方差法)复选项,此时“Display(显示)”栏中的“Rotated Solution(旋转后的解)”将被激活为系统默认态,选中“Loading Plot(s)(载荷图)”复选项,将会在输出结果中给出因子载荷图式。
- 最大方差法是一种正交旋转,该方法使得每一个因子中具有高载荷值的变量尽可能地减少,方差贡献因此趋向于均衡,这样可以简化因子解释过程。
- 最大收敛迭代次数,系统默认的25 次,如果数据变量较多或样本较大,经过25 次迭代可能计算过程仍然未能收敛,需要改为50 次、100 次乃至更多,否则SPSS 无法给出计算结果。迭代次数越多,计算时间也就越长。在多数情况下,不足25 次迭代计算过程就会收敛。
图7-4设置“旋转”选项卡
3、因子分析结果解读。在输出结果中,前面的基础内容与主成分分析的是类似的,在成分矩阵后就有所不同。
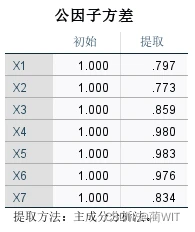
图7-5公因子方差表
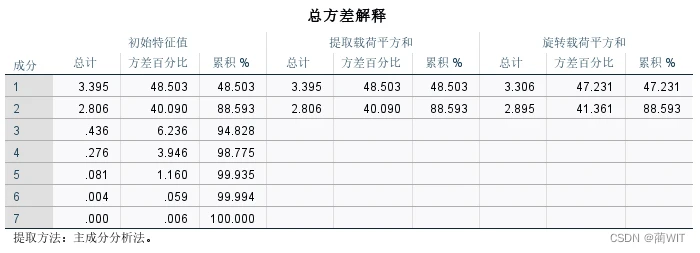
图7-6总方差解释表
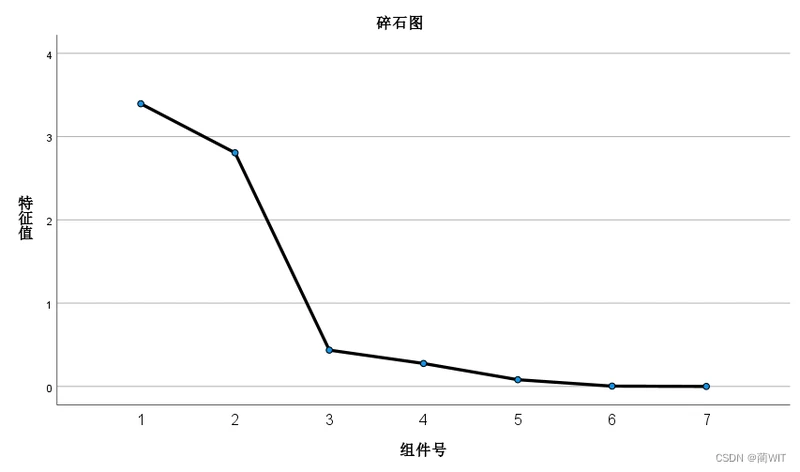
图7-7碎石图
- 数据的主成分的数目可以根据相关系数矩阵的特征根来判定。相关系数矩阵的特征根刚好等于主成分的方差,而方差是变量数据蕴涵信息的重要判据之一。根据前面主成分分析中原则以及因子分析的结果图表,可以得出该数据的主成分的个数为2,第一主成分可取X4的信息,第二主成分可取X5、X6的信息:
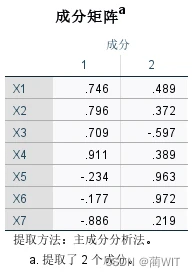
图7-8成分矩阵表(主因解载荷矩阵)
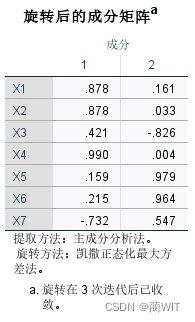
图7-9旋转成分矩阵(正交旋转后的主因解载荷矩阵)
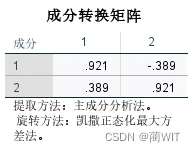
图7-10成分转换矩阵
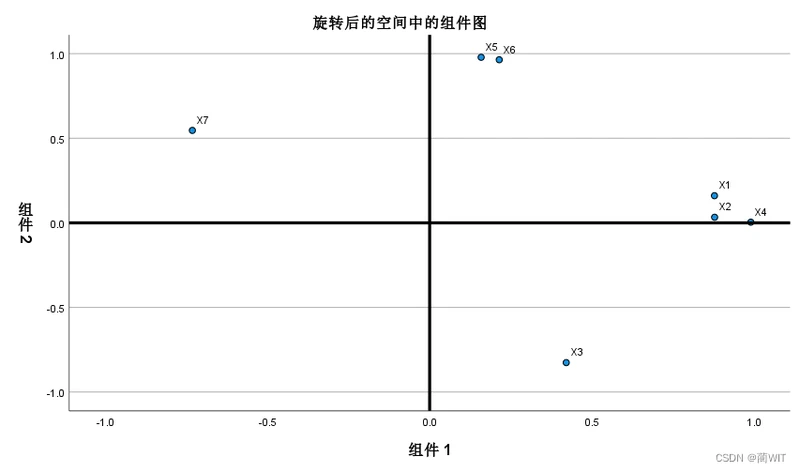
图7-11旋转后的空间中的组件图
实验八 地统计分析
一、实验目的:掌握地统计分析的定义、内涵,重点掌握地统计分析的计算步骤、利用所给数据能够建立地统计分析思路与结果,并能够进行检验。
二、实验内容:运用ArcGIS应用软件中的相关的模块,利用所给的相关的数据,用半变异函数进行分析。
图8-0站点NO2浓度数据(部分)
三、实验步骤与结果分析:
1、数据可视化。将所给的原始数据加载到ArcGIS中显示出来。
图8-1数据点的空间分布状态(标注值为NO2浓度)
2、利用【Geostatistical Analyst】模块进行地统计分析。利用【探索数据】中的相关功能操作对数据进行初步判断。
图8-2地统计分析模块
- 在直方图中,可以查看到数据的分布状况,以及其是否满足正态分布。在图的右上角还列出了一些相关指数统计,其中偏度指数为0.96009,其越接近0说明数据越接近正态分布。
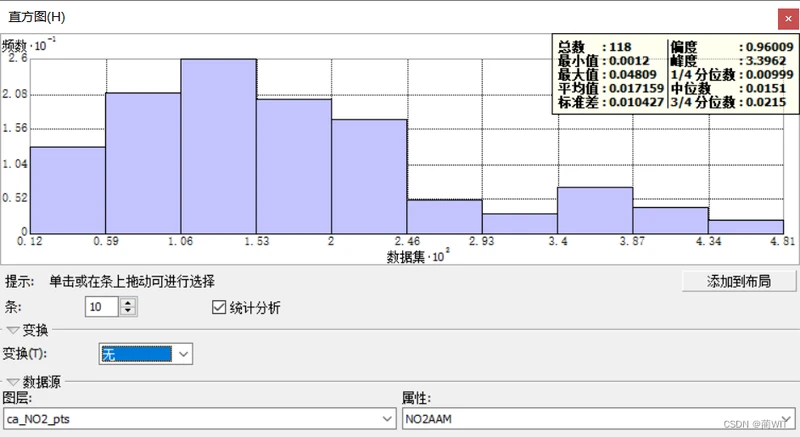
图8-3直方图
- 正态QQ图也是用来分析数据是否服从正态分布,点主要分布在直线附近时,说明数据是服从正态分布。
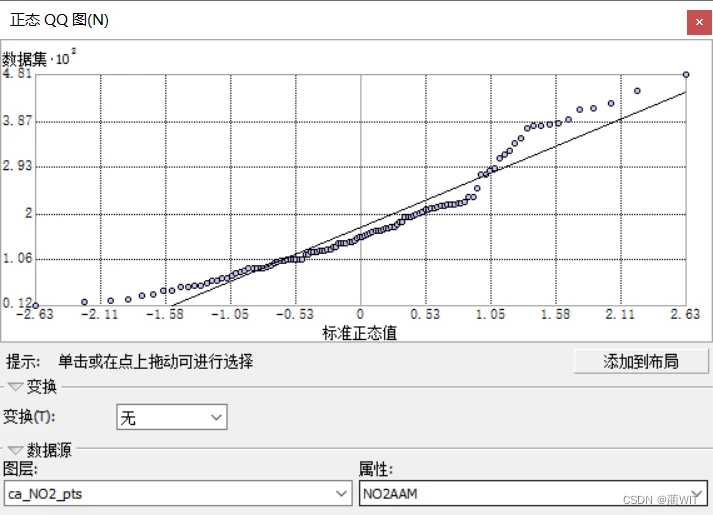
图8-4正态QQ图
- 趋势分析用于检测数据是否存在趋势分布。
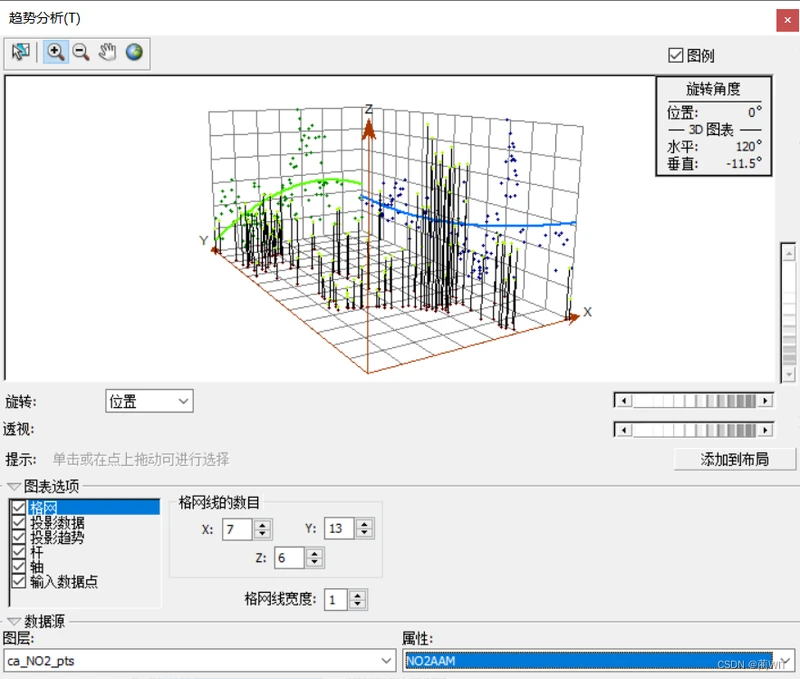
图8-5趋势分析
- 半变异云图,是对地理现象具有的空间相关特性的定量化表示。半变异函数/协方差云工具可以用来检查数据集中空间自相关的局部特征以及查找局部异常值。如果存在空间相关性,则距离较近的点对(在 x 轴的最左侧)应具有较小的差值(在 y 轴上的值较小)。随着各个点之间的距离越来越大(点在 x 轴上向右移动),通常,差值的平方也应随之增大(在 y 轴上向上移动)。通常,平方差超过某个距离后就会保持不变。超过这个距离的位置对被视为不相关。如果半变异函数中的点对构成一条水平的直线,那么数据中可能不存在空间自相关,因而对数据进行插值也就失去了意义。
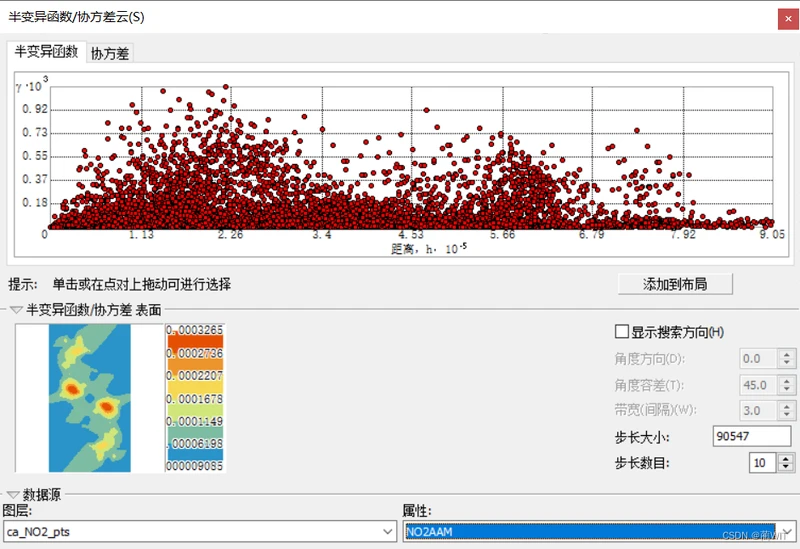
图8-6半变异云图
3、利用【地统计向导】进行插值分析。选择常用的普通克里金插值方法,因为在趋势分析图上可以看出数据在两个方向上都具有趋势,所以阶数选择“二次”.
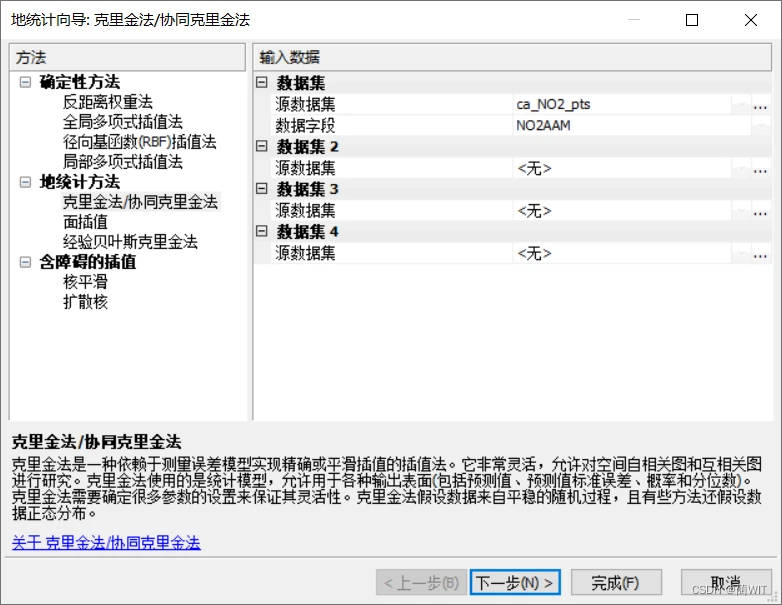
图8-7地统计向导
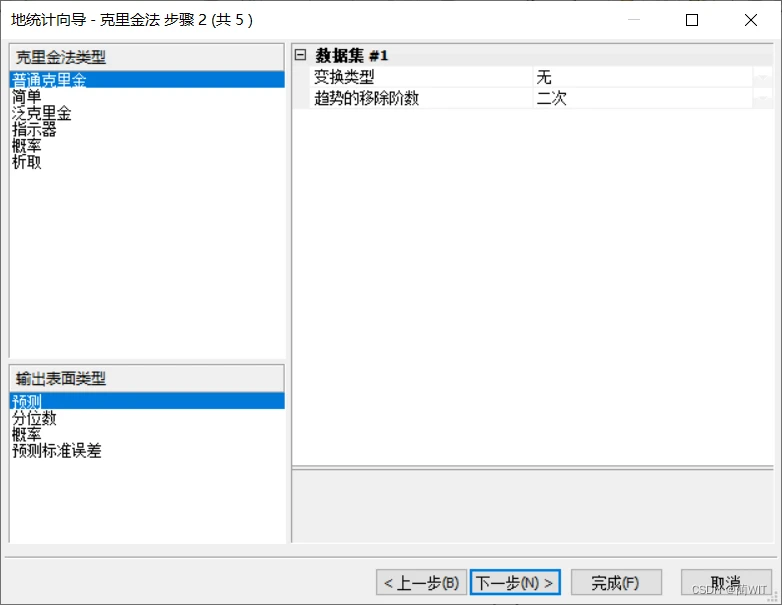
图8-8选择克里金插值类型
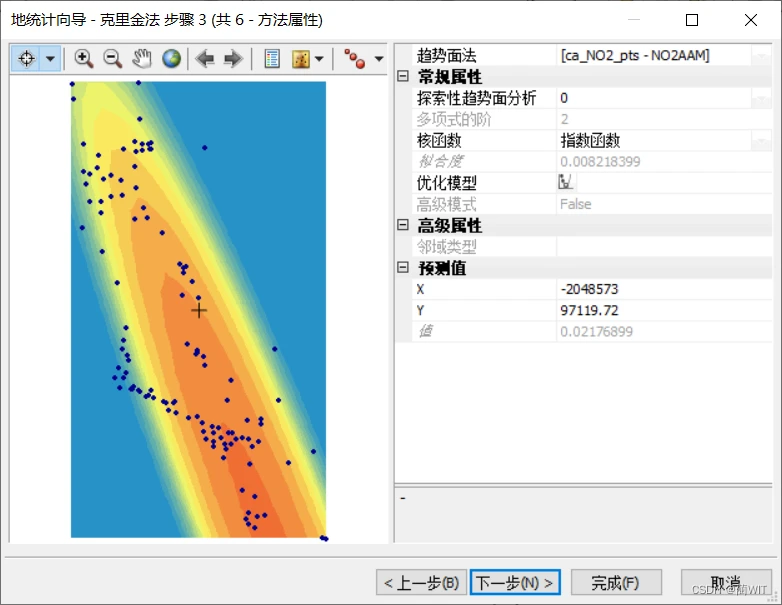
图8-9设置方法属性
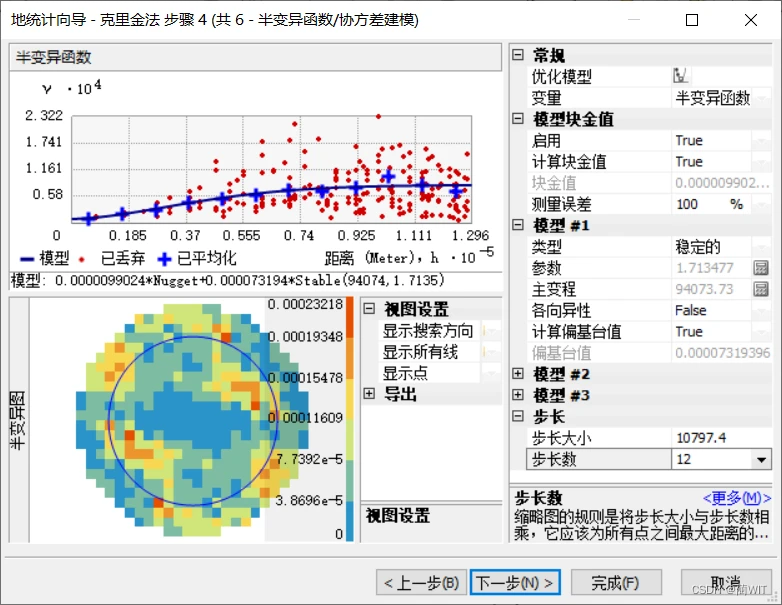
图8-10半变异函数建模
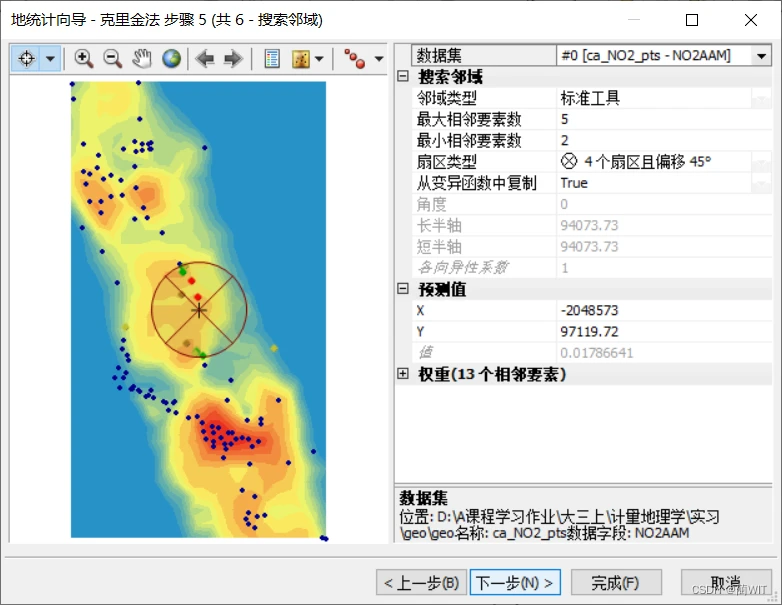
图8-11搜索邻域
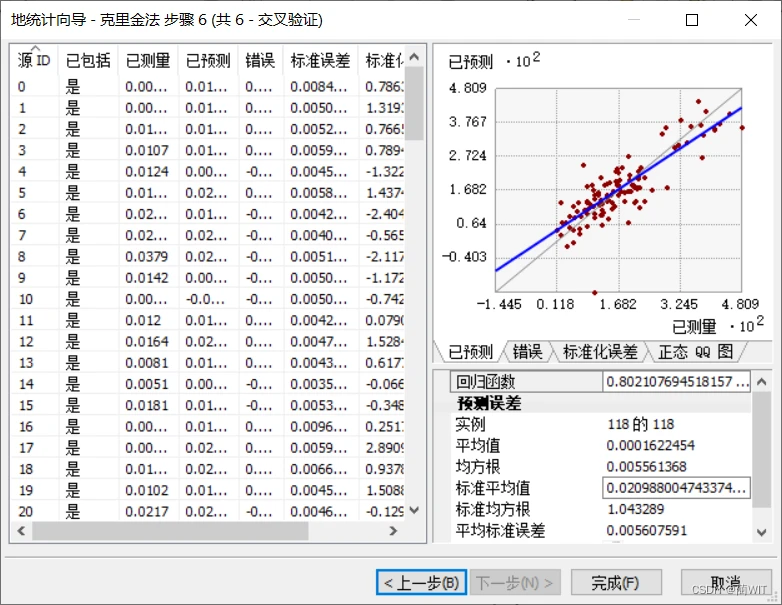
图8-12交叉验证
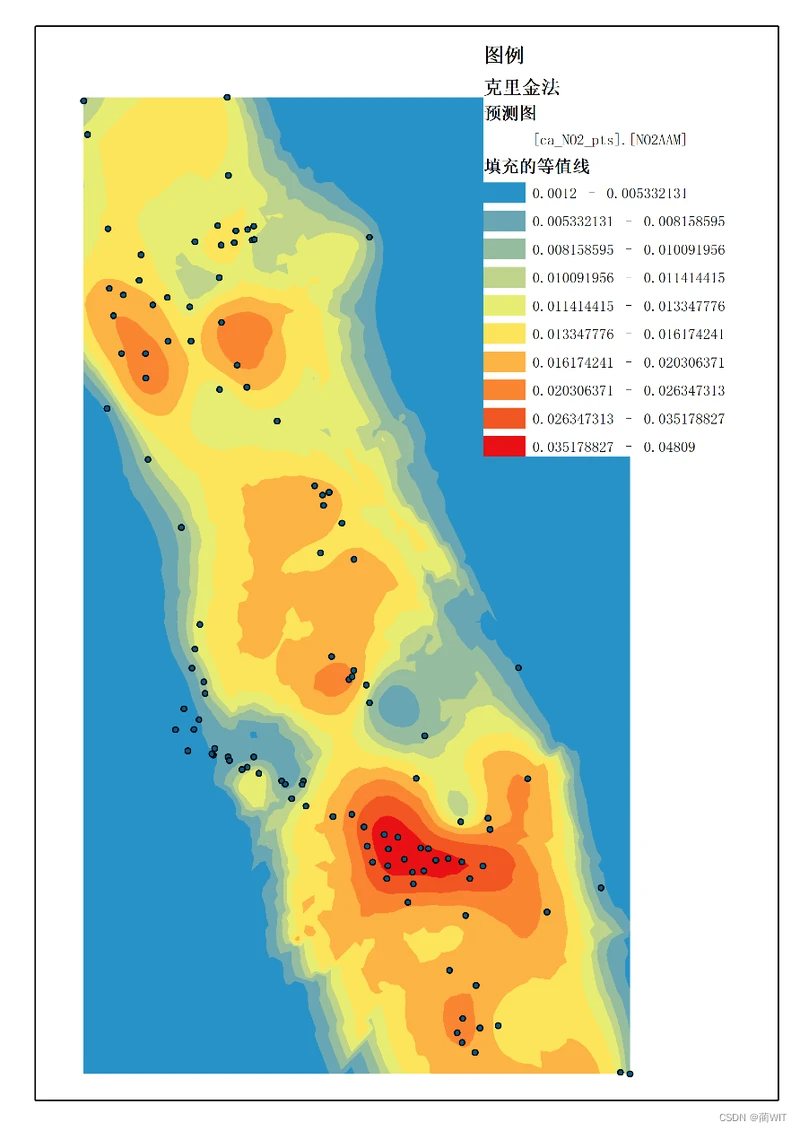
图8-13克里金插值结果预测图
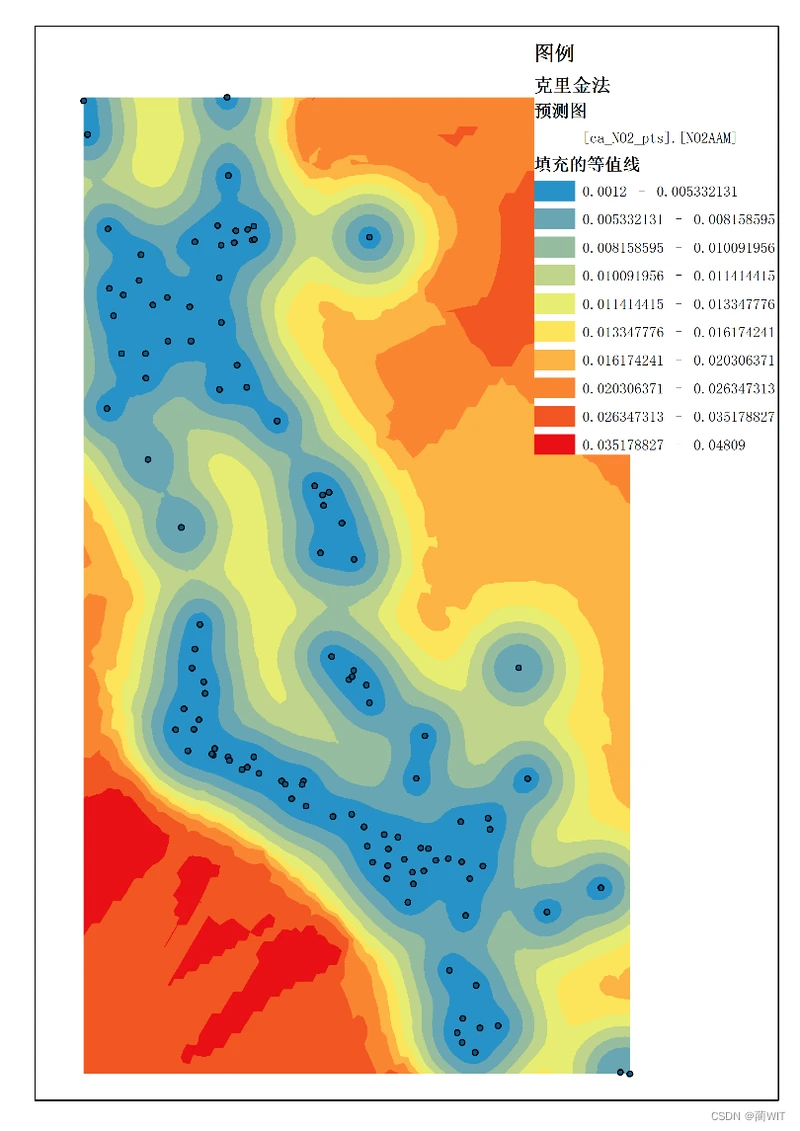
图8-14预测标准误差图
实验九 趋势面分析
一、实验目的:掌握趋势面分析的定义、内涵,重点掌握趋势面分析的计算步骤、利用所给数据能够建立趋势面分析思路与结果,并能够进行检验。
二、实验内容:运用SPSS和ArcGIS应用软件中的相关的模块与工具,利用表中的数据,进行趋势面分析。
表8 空间单元人口密度数据
| 空间单元序号 | 人口密度(人/km) | 公里网坐标x(单位:米) | 公里网坐标y(单位:米) |
| 1 | 2695 | 5260.54 | 2385.21 |
| 2 | 4445 | 3707.82 | 2340.77 |
| 3 | 1739 | 1843.69 | 2342.78 |
| 4 | 4043 | 5032.75 | 2265.98 |
| 5 | 3342 | 5709.87 | 1978.19 |
| 6 | 1960 | 4625.16 | 2296.62 |
| 7 | 2282 | 2656.67 | 2254.06 |
| 8 | 2064 | 4319.76 | 2291.54 |
| 9 | 3034 | 3415.9 | 2248.6 |
| 10 | 3272 | 4092.21 | 2161.05 |
| 11 | 2383 | 4838.59 | 2259.9 |
| 12 | 3176 | 5263.07 | 1934.01 |
| 13 | 2685 | 1578.79 | 2193.84 |
| 14 | 4002 | 2797.76 | 2166.17 |
| 15 | 4516 | 1971.07 | 2123.61 |
| 16 | 2941 | 4578.13 | 1897.78 |
| 17 | 2532 | 3631.43 | 2140.09 |
| 18 | 2681 | 4285.84 | 2128.63 |
| 19 | 1254 | 2445.62 | 2096.58 |
| 20 | 3055 | 3176.42 | 2146.64 |
| 21 | 3062 | 4663.75 | 2151.41 |
| 22 | 2637 | 4023.81 | 1868.53 |
| 23 | 3952 | 2225.93 | 2040.77 |
| 24 | 2771 | 4886.63 | 1863.7 |
| 25 | 2096 | 2951.19 | 2066.23 |
| 26 | 3224 | 3407.66 | 1797.43 |
| 27 | 3819 | 1639.67 | 1909.3 |
| 28 | 2448 | 2078.15 | 1914.68 |
| 29 | 2594 | 2739.6 | 1961.79 |
| 30 | 2303 | 1783.46 | 1910.66 |
| 31 | 9628 | 3018.15 | 1869.9 |
| 32 | 1742 | 2425.15 | 1828.76 |
| 33 | 2492 | 1992.52 | 1814.27 |
| 34 | 2897 | 2566.68 | 1819.99 |
| 35 | 2544 | 3009.65 | 1548.92 |
| 36 | 3099 | 2802.02 | 1770.38 |
| 37 | 3562 | 2132.38 | 1657.93 |
| 38 | 2689 | 2720.85 | 1685.62 |
| 39 | 4321 | 5773.06 | 1335.66 |
| 40 | 3325 | 1823.64 | 1647.76 |
| 41 | 2103 | 2618.31 | 1646.93 |
| 42 | 2308 | 2573.41 | 1390.76 |
| 43 | 2387 | 1636.73 | 1411.35 |
| 44 | 4129 | 2252.13 | 1463.33 |
| 45 | 3123 | 2040.32 | 1462.2 |
| 46 | 4907 | 4018.33 | 1023.25 |
| 47 | 4215 | 4657 | 1128.29 |
| 48 | 2535 | 1842.43 | 1428.36 |
| 49 | 2569 | 2157.29 | 1234.85 |
| 50 | 281 | 3212.67 | 431.96 |
三、实验步骤与结果分析:
1、数据转矢量,利用ArcGIS进行初步分析。打开ArcGIS软件,通过添加XY坐标的方法,将数据以矢量点的形式添加到图层中显示;利用【Geostatistical Analyst】模块中的【探索数据】分析其趋势。
图9-1添加XY数据

图9-2数据点的空间分布状况
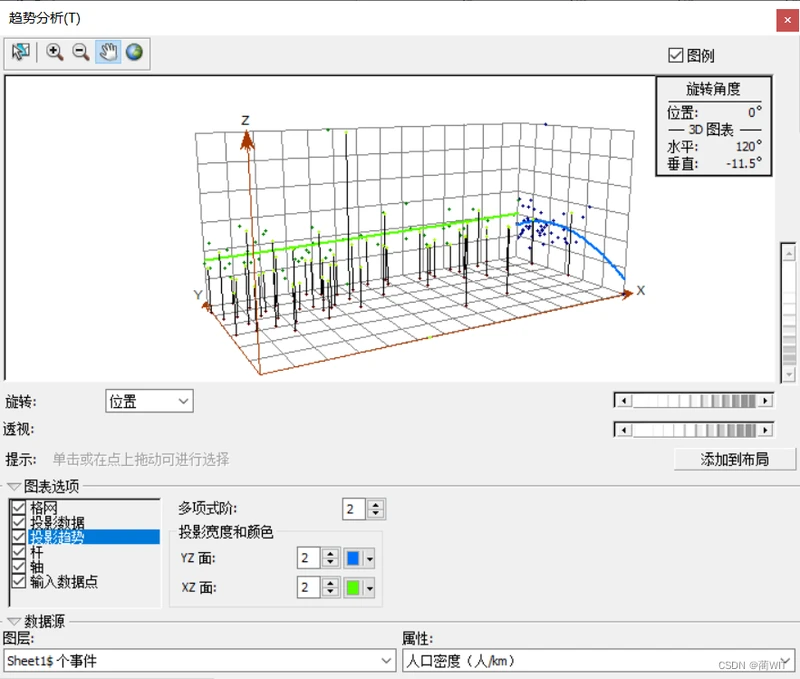
图9-3趋势分析
- 如图9-3,数据中的人口密度分布在东西方向趋势不明显,而在南北方向具有较明显的趋势,可以看出从南到北,人口密度是先缓慢增加后迅速减少的。
2、进行趋势面插值分析。利用ArcCatalog工具箱中的【趋势面分析】工具创建趋势面图层,进一步进行分析与检验。
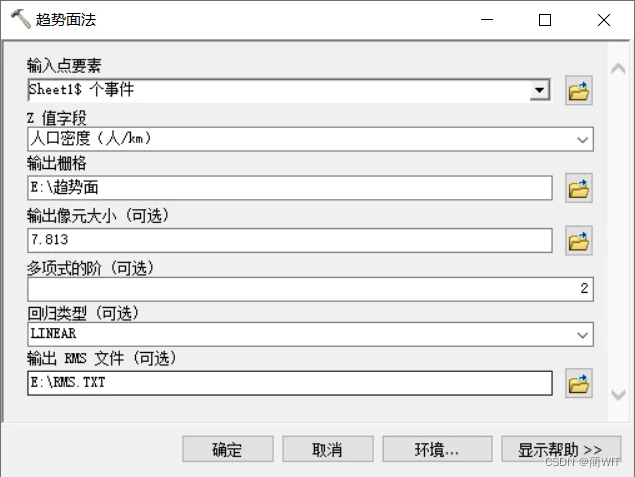
图9-4趋势面法插值分析
- 使用趋势面法将点插值成栅格表面。这里的Z值字段为存放每个点的高度值或量级值的字段,选择“人口密度”;多项式的阶数设为:2(二阶多项式);回归类型选择:LINEAR—对输入点进行最小二乘曲面拟合,这种类型适用于连续型数据。选择输出RMS文件:包含插值的 RMS 误差和卡方相关信息的输出文本文件的文件名。

图9-5趋势面插值结果图(矢量点标注的数值为人口密度值)
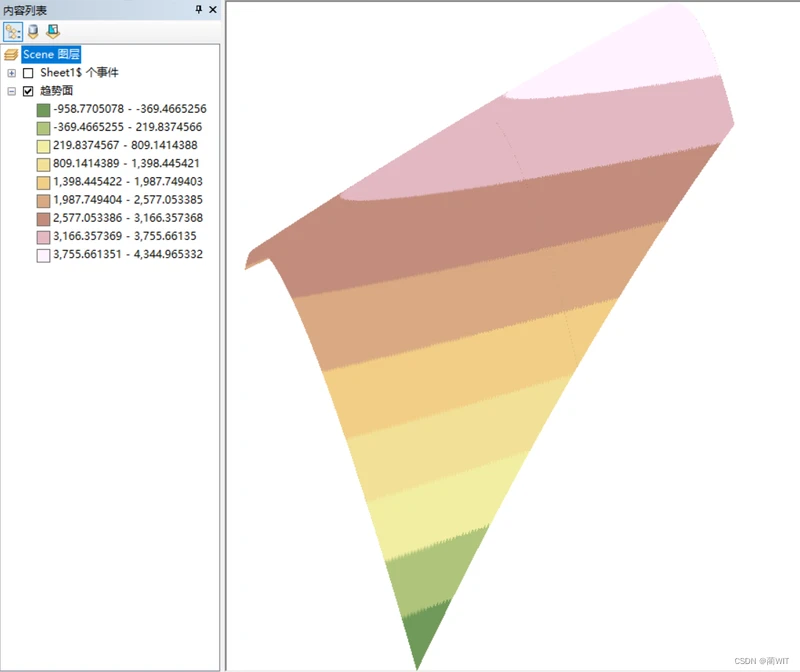
图9-6按照趋势值拉伸后的趋势面
- 从上面趋势面插值图可以直观看出,其人口密度分布趋势与前面“趋势分析”结论相符合:南北方向具有较明显的趋势。
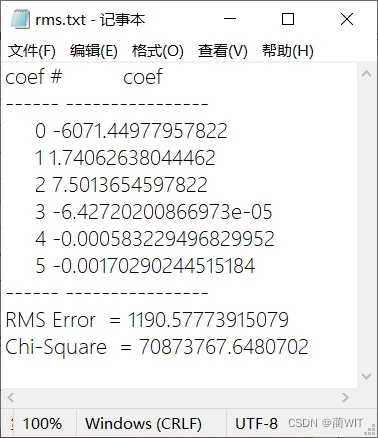
图9-7输出的RMS文件
- 在如图9-7的RMS文件中,可以看出其采用的二阶多项式的六个系数,即0到5对应的值,以及插值的RMS误差:1190.57773915079,卡方相关信息:70873767.6480702。据此可以写出其二阶趋势面模型:
z = -6071.44977957822+ 1.74062638044462x+ 7.5013654597822y -6.42720200866973e-05x²-0.000583229496829952xy -0.00170290244515184y²
3、利用SPSS进行趋势面回归分析。先算出x²,y²,xy作为变量,进行多元线性回归分析,计算二阶回归方程,同时进行误差诊断与评估。
图9-8导入处理数据
图9-9线性回归参数设置
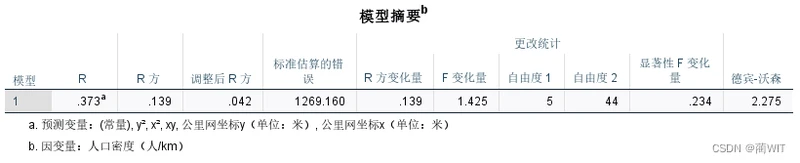
图9-10模型摘要
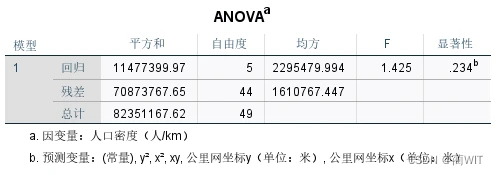
图9-11 ANOVA残差统计图
- 从系数表中可以看出,其与前面在ArcGIS中算得的二阶多项式的六个系数是一致的。
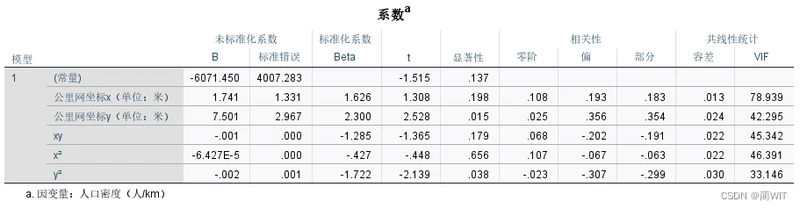
图9-12系数表
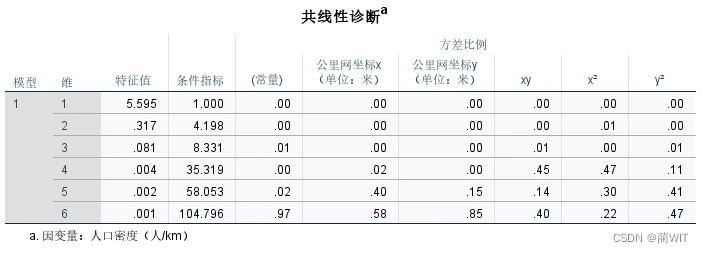
图9-13共线性诊断表
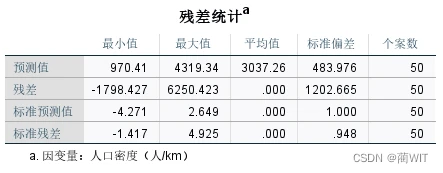
图9-14残差统计表
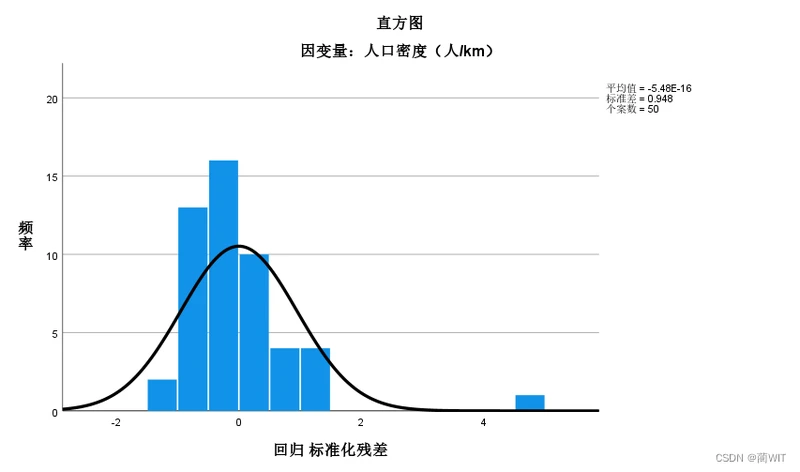
图9-15回归残差直方图
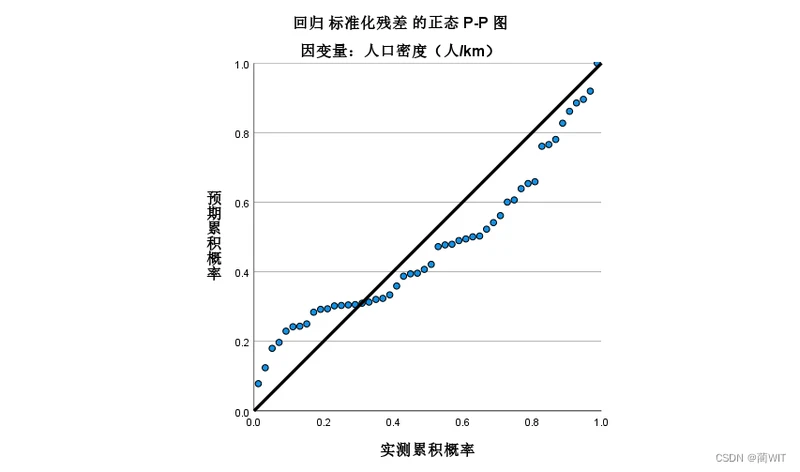
图9-16回归标准化残差的正态P-P图
实验十 马尔可夫分析
一、实验目的:掌握马尔可夫分析的定义、内涵,重点掌握马尔可夫分析的计算步骤、利用所给数据能够建立马尔可夫分析思路与结果,并能够进行检验。
二、实验内容:运用Excel应用软件中的相关的功能操作,利用表中的某地区农业收成变化状态转移情况数据,请据此对2030年的农业收成状况进行预测。
表9 某地区农业收成变化状态转移情况表
| 年份 | 1965 | 1966 | 1967 | 1968 | 1969 | 1970 | 1971 | 1972 | 1973 | 1974 |
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 状态 | E1 | E1 | E2 | E3 | E2 | E1 | E3 | E2 | E1 | E2 |
| 年份 | 1975 | 1976 | 1977 | 1978 | 1979 | 1980 | 1981 | 1982 | 1983 | 1984 |
| 序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 状态 | E3 | E1 | E2 | E3 | E1 | E2 | E1 | E3 | E3 | E1 |
| 年份 | 1985 | 1986 | 1987 | 1988 | 1989 | 1990 | 1991 | 1992 | 1993 | 1994 |
| 序号 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 状态 | E3 | E3 | E2 | E1 | E1 | E3 | E2 | E2 | E1 | E2 |
| 年份 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 |
| 序号 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 状态 | E1 | E3 | E2 | E1 | E1 | E2 | E2 | E3 | E1 | E2 |
三、实验步骤与结果分析:
1、数据预处理。将所给的原始数据进行处理,统计三种状态的变化情况的数量,并计算出状态转移概率矩阵,并将其录入到Excel表格中。
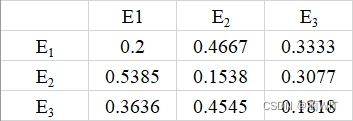
图10-1状态转移概率矩阵
2、转移概率矩阵的自乘运算。通过选定单元格,利用“MMULT()”函数逐步进行矩阵的自乘运算,直到出现稳定分布为止。
逐步自乘计算的公式为:![]()
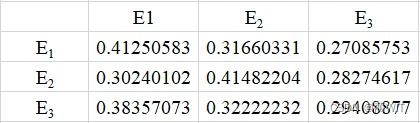
图10-2第一步自乘运算结果
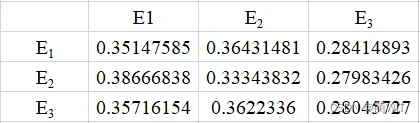
图10-3第二步自乘运算结果
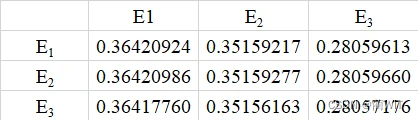
图10-4第八步自乘运算结果
- 稳定分布在第几步出现,取决于数据精度的要求。如果保留小数点后4位,则上第八步即出现稳定分布,四舍五入后为如图10-5。
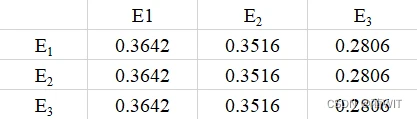
图10-5最后的稳定分布(精度为保留四位小数)
3、状态概率行向量的计算(马尔可夫预测法)。由原始数据可知,最新一年(2004年)的收成状态为E2,因此设置2004年的农业收成状态为[0,1,0],将此矩阵与2004年的状态转移概率矩阵相乘,得到下一年份的状态概率,依此计算,可得到2030年的状态概率。
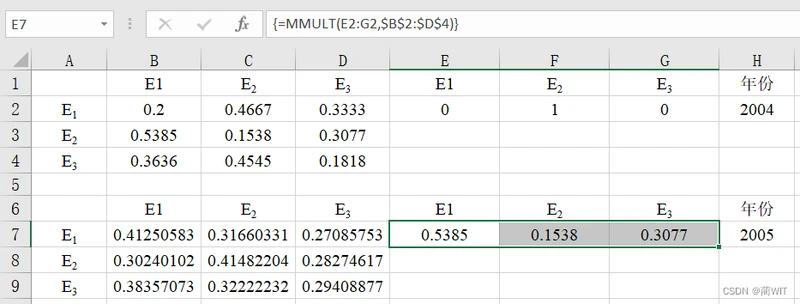
图10-6计算状态概率行向量操作(部分)
- 如图10-7为2030年的状态概率预测值。2030年农业收成状态为E1的概率为0.36526783,状态为E2的概率为0.352614087,状态为E3的概率为0.281411693,据此可知,在2030年农业收成状态为E1的可能性最大。
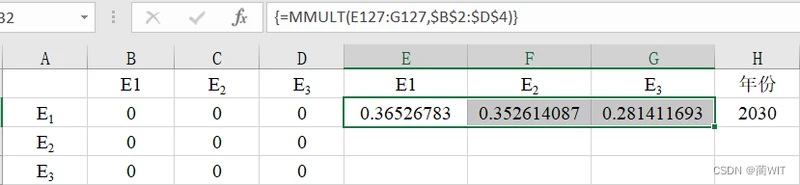
图10-7农业收成状态2030年概率预测值
