前言

温馨提示：为了更好的阅读体验，建议通过PC端阅读。

省流助手：直接把结论贴出来，种植示例在文章最后一部分（吐槽一下B站专栏什么时候可以出一个目录跳转功能）

接下来就请收下这份来自理科生的礼物吧！(。-ω-)zzz

摘要：农作物从被播种到成熟的过程共有5个节点，分别是种子、萌芽、小、中和成熟，每两个节点之间是一个生长阶段，共有4个生长阶段。每一个阶段结束时，农作物会立刻进行一次结算。

饥荒联机版的耕地中一共蕴含有3种养分，分别是催长剂、堆肥和粪肥，每种农作物在每个生长阶段结束进行结算时，都会同时对这三种养分产生影响，影响分为向耕地释放或从耕地中吸收，而农作物的养分之间的循环关系正是通过“耕地”这一桥梁来实现的。假设一块耕地中种了一棵农作物A和一棵农作物B，农作物A在每次生长结算时从土地中吸收1单位催长剂，而农作物B每次生长结算时恰好向土地释放1单位催长剂，那么这两种农作物就刚好可以实现养分的自给自足，从而整个生长过程无需施肥。

那么不同的农作物要如何安排种植的比例才能刚好实现这种自给自足的效果呢？接下来本文将从数学建模的角度，详细进行介绍。

关键词：饥荒联机版巨大农作物种植搭配线性代数优化组合

一、农作物基本情况介绍

首先介绍一下各种农作物生长对养分的需求。

每个农作物的产品下面有三栏介绍，其中第一栏为适宜生长的季节，第二栏为水消耗，第三栏为养分循环。在养分循环中，每种农作物生长过程中都会涉及到三种养分，从左到右依次为：催长剂、堆肥、粪肥，每种养分后面有箭头，箭头向下表示向土地释放，向上表示从土地中吸收，并且1个箭头表示每个生长阶段结算时吸收或释放1个单位，2个箭头表示吸收或释放2个单位，以此类推。

不妨规定向耕地释放养分为+，从耕地吸收为-，并且将养分情况完全一致的农作物看作是“等效农作物”，并将等效农作物合并为一种农作物看待，因为等效农作物在种植时可以相互替代。例如春天，芦笋蕨和玉米杆都是释放1单位催长剂，吸收2单位堆肥，释放1单位粪肥，所以就互为等效农作物。将农作物的养分数据按季节整理如下：

值得注意的是，不可以在一块养分贫瘠的耕地上种植。原因是，养分的自给自足是一种动态平衡，农作物合理搭配种植可以使耕地中的养分始终维持在一个充足的水平，但不能使耕地中的养分变多。具体来讲，假设耕地中的催长剂在播种之前就是0，农作物A每次生长释放2点催长剂，农作物B每次生长吸收2点催长剂。如果农作物B先于农作物A进入下一生长阶段，那么B此次结算时会因为耕地种催长剂为0从而无法为农作物B提供足够的养分，于是农作物B就会增加1点压力值。尽管后面农作物A生长时可以释放2点催长剂，但农作物B本阶段的判定已经结束，无法弥补。如此几个生长阶段累积下来，一旦压力值大于等于2，就无法成为巨大农作物了。

二、线性模型的建立与求解

有了这些数据之后，我们首先能想到的办法就是用计算机列举出所有可能的种植情况，然后筛选出重复的情况再进行化简，就可以得到所有想要的结果。但是，粗略估计一下，仅以春天为例，为保证农作物不会拥挤，一块耕地最多可以挖10个坑，每个坑种植的农作物有8种可供选择，加上每个坑都可以不种植农作物，这样每个坑就有9种可能出现的情况，于是每块耕地上可能出现的种植情况就有 $9%5E%7B10%7D%3D3486784401$ 种可能性！而且这仅仅是春天一个季节。显然，枚举法是不现实的。

设养分矩阵为 $A$ ，每种农作物数量的向量为 $%5Cvec%7Bx%7D%20$ ，由于目标是使养分刚好互补，所以一块耕地中所有农作物吸收和释放的养分之和应当为0，由此可以建立数学模型：

$A%5Cvec%7Bx%7D%20%3D%5Cvec%7B0%7D%20$

此模型是一个齐次线性方程组，适用于所有季节，求解此方程组，并找到解集中所有的自然数解，写成比例的形式，再化成最简整数比，即可得到理论上所有的搭配方案。

以冬天为例，假设一块耕地中，芦笋蕨、大蒜植株、土豆植株、胡萝卜植株/南瓜植株的数量分别为 $x_1%2Cx_2%2Cx_3%2Cx_4$ ，可以得到：

$A%3D%5Cbegin%7Bbmatrix%7D%0A%201%20%26%20-2%20%26%202%20%26%201%5C%5C%0A%20-2%20%26%201%20%26%20-4%20%26%201%5C%5C%0A%201%20%26%201%20%26%202%20%26%20-2%0A%5Cend%7Bbmatrix%7D%2C%0A%5Cvec%7Bx%7D%20%3D%5Cbegin%7Bbmatrix%7D%0A%20x_%7B1%7D%20%5C%5C%0A%20x_%7B2%7D%20%5C%5C%0A%20x_%7B3%7D%20%5C%5C%0A%20x_%7B4%7D%20%5C%5C%0A%5Cend%7Bbmatrix%7D$

其中矩阵 $A$ 实际上是将上面农作物养分表里展示的养分给 “转置” 一下，也就是沿着135°斜线翻转一下。将其代入 $A%5Cvec%7Bx%7D%20%3D%5Cvec%7B0%7D%20$ 并展开即可得到

$%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%0A%20%5Cbegin%7Balign*%7D%0A%20%20x_%7B1%7D-2x_%7B2%7D%2B2x_%7B3%7D%2Bx_%7B4%7D%3D0%20%5C%5C%0A%20%20-2x_%7B1%7D%2Bx_%7B2%7D-4x_%7B3%7D%2Bx_%7B4%7D%3D0%20%5C%5C%0A%20%20x_%7B1%7D%2Bx_%7B2%7D%2B2x_%7B3%7D-2x_%7B4%7D%3D0%0A%20%5Cend%7Balign*%7D%0A%5Cend%7Bmatrix%7D%5Cright.$ （1）

由于系数矩阵 $A$ 的秩为2，而变量个数为4，秩亏，因此该方程组有无穷多解。实际上，四个季节列出的方程组均有无穷多解。接下来，有两种方式解决此方程组。

方法一：

以中学知识便可得知，这是一个包含3个方程的四元一次方程组，是没有唯一解的，但是，如果我们先只考虑其中三种农作物的搭配方式，而剩下的农作物先不做考虑，那么就相当于人为地先让一个变量等于0，比如先只考虑芦笋蕨、胡萝卜/南瓜植株、土豆植株这三种农作物的搭配而暂时不考虑大蒜植株，也就是令 $x_%7B3%7D%20%3D0$ ，那么方程组就变成了

$%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%0A%20%5Cbegin%7Balign*%7D%0A%20%20x_%7B1%7D-2x_%7B2%7D%2Bx_%7B4%7D%3D0%20%5C%5C%0A%20%20-2x_%7B1%7D%2Bx_%7B2%7D%2Bx_%7B4%7D%3D0%20%5C%5C%0A%20%20x_%7B1%7D%2Bx_%7B2%7D-2x_%7B4%7D%3D0%0A%20%5Cend%7Balign*%7D%0A%5Cend%7Bmatrix%7D%5Cright.$

这样一来，原方程组就变成了一个含有3个方程的三元一次方程组，有可能求出唯一解（含有3个方程的三元一次方程组也不一定有唯一解，如果方程之间存在线性相关，则依然有无穷多解）。将 $x_%7B3%7D%20%3D0$ 也算在解里面，那么就可以解得

$%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%0A%20x_%7B1%7D%3D1%20%5C%5C%0A%20x_%7B2%7D%3D1%20%5C%5C%0A%20x_%7B3%7D%3D0%20%5C%5C%0A%20x_%7B4%7D%3D1%20%0A%5Cend%7Bmatrix%7D%5Cright.$

接下来按照这个做法，每3种农作物都考虑一遍，那么一共就可以重建出4个新的方程组，对每一个方程组都进行求解，如果有唯一解，再观察这个解的特点，如果含有负数，舍去，因为农作物种植的数量不可能为负值，如果4个变量全为0，也就是求出了一个零解，也舍去，因为零解意味着什么都不种，没有意义。最后从还剩下的解里面，将解写成比例的形式，再化简成整数比例的形式即可。比如刚才求出的这个解的含义就是：

芦笋蕨：胡萝卜植株/南瓜植株：土豆植株 = 1：1：1

大家可以自行验证。

以上做法如果用数学语言来描述的话，那就是，对于系数矩阵有 m 行 n 列的线性方程组，任取 m 个变量作为基变量，其余的变量作为非基变量，并令所有的非基变量为0，构建一个新的线性方程组。例如，在前面的例子中，就选取了 $x_%7B1%7D%20%2Cx_%7B2%7D%20%2Cx_%7B4%7D%20$ 作为基变量，而 $x_%7B3%7D%20$ 为非基变量，并且令 $x_%7B3%7D%20%3D0$ 。如果方程组满秩，那么一定可以求出唯一解，这个唯一解就是原方程组的一个基本解。

求出一个基本解之后，还需要验证此基本解是否为基本可行解，因为有些时候求出的基本解可能为负值，然而种植某种农作物的数量不可能为负值。之后，再将基本可行解中的零解舍去，因为零解对种植来讲没有任何意义。最后，将基本可行解写成比例的形式并化简为整数即可。

利用方法一求解时，如果系数矩阵有 m 行 n 列（m 为养分的种类数，实际上只能为3，n 为某一季节所有应季农作物的种类数），那么显然可以构建出 $C_%7Bn%7D%5E%7Bm%7D%20%3D%5Cfrac%7Bn!%7D%7Bm!(n-m)!%7D%20$ 个新的线性方程组，但这些新的方程组中并不是所有的都有唯一解，因为方程之间可能存在线性相关，一旦方程线性相关，则必然秩亏，从而会有无穷多解。

因此，完整的求解步骤如下

构建出所有 $C_%7Bn%7D%5E%7Bm%7D%20$ 个新的线性方程组；
从中筛选出所有的满秩方程组，齐次线性方程组判断满秩的方法为系数矩阵 $A$ 的秩等于变量个数m，而对于非齐次线性方程组 $A%5Cvec%7Bx%7D%20%3D%5Cvec%7Bb%7D%20$ 的判断方法为 $rank(A)%3Drank(%5Cbegin%7Bbmatrix%7D%0AA%2C%5Cvec%7Bb%7D%0A%5Cend%7Bbmatrix%7D)%3Dm$ ；
对筛选出的方程组求解，得出所有的基本解；
从求得的基本解中筛选出所有的基本可行解，再从基本可行解中去掉零解，因为零解意味着什么都不种；
将最终保留下来的基本可行解写成比例的形式，再化简为最简整数比。

对所有的季节，建立 $A%5Cvec%7Bx%7D%20%3D%5Cvec%7B0%7D%20$ 之后，都重复这个步骤，即可得到所有的农作物搭配方案。

方法二：

这个方法的基本思路是先求出齐次线性方程的通解，再尝试找出所有符合条件的特解。

先求出方程组（1）的基础解系为

$%5Cbegin%7Bbmatrix%7D%0A%20%5Cvec%7B%5Cxi_%7B2%7D%7D%20%2C%5Cvec%7B%5Cxi_%7B2%7D%7D%20%0A%5Cend%7Bbmatrix%7D%0A%3D%5Cbegin%7Bbmatrix%7D%0A%20-2%20%26%201%5C%5C%0A%200%20%26%201%5C%5C%0A%201%20%26%200%5C%5C%0A%200%20%26%201%0A%5Cend%7Bbmatrix%7D$

基础解系包含的两个特解为

$%5Cvec%7Bx_%7B1%7D%7D%20%20%3D%20%5Cvec%7B%5Cxi_%7B1%7D%7D%3D%0A%5Cbegin%7Bbmatrix%7D%0A-2%20%5C%5C%0A0%20%5C%5C%0A1%20%5C%5C%0A0%0A%5Cend%7Bbmatrix%7D%2C%0A%5Cvec%7Bx_%7B2%7D%7D%20%3D%20%5Cvec%7B%5Cxi_%7B2%7D%7D%3D%0A%5Cbegin%7Bbmatrix%7D%0A1%20%5C%5C%0A1%20%5C%5C%0A0%20%5C%5C%0A1%0A%5Cend%7Bbmatrix%7D$

由此得出原方程组的通解为

$%5Cvec%7Bx%7D%20%3D%20k_%7B1%7D%5Cvec%7B%5Cxi_%7B1%7D%7D%2Bk_%7B2%7D%5Cvec%7B%5Cxi_%7B2%7D%7D%0A%3D%20k_%7B1%7D%5Cbegin%7Bbmatrix%7D%0A-2%20%5C%5C%0A0%20%5C%5C%0A1%20%5C%5C%0A0%0A%5Cend%7Bbmatrix%7D%0A%2Bk_%7B2%7D%5Cbegin%7Bbmatrix%7D%0A1%20%5C%5C%0A1%20%5C%5C%0A0%20%5C%5C%0A1%0A%5Cend%7Bbmatrix%7D$ （2）

其中 $k_%7B1%7D%2Ck_%7B2%7D$ 为任意实数，即随便找两个数代进去，都可以得到方程的一个解，只要解的每个元素均为自然数且不全为0，再将解化简为整数形式，即可得到一种搭配方案。比如取 $k_%7B1%7D%3D0%2Ck_%7B2%7D%3D1$ ，即可得到方程组的一个特解为

$%5Cvec%7Bx_%7B1%7D%7D%20%3D%5Cbegin%7Bbmatrix%7D%0A1%20%5C%5C%0A1%20%5C%5C%0A0%20%5C%5C%0A1%0A%5Cend%7Bbmatrix%7D$

这个特解意味着，芦笋蕨：胡萝卜植株/南瓜植株：土豆植株 = 1：1：1，大家可以自行验证。

通解求出后，我们已经在理论上初步找出了冬天的农作物所有可能的搭配方式。然而到此为止，问题还没有得到真正解决，因为不难发现，只有给出具体的 $%5Cvec%7Bk%7D$ 的值（也就是本例中的 $%5Cvec%7Bk_1%7D%2C%5Cvec%7Bk_2%7D$ ，哪怕是随便给的），代入求出特解，才是真正对农作物的种植搭配有指导意义的。如果你此时有一个疑问：“我怎么知道 $k_%7B1%7D%2Ck_%7B2%7D$ 该取多少哇？”那么恭喜你，你已经理解了以上的论证，并且发现了问题的关键。接下来，本文就详细阐述 $k_%7B1%7D%2Ck_%7B2%7D$ 究竟该如何取值。

不难发现，如果把基础解系 $%5Cbegin%7Bbmatrix%7D%0A%20%5Cvec%7B%5Cxi_%7B2%7D%7D%20%2C%5Cvec%7B%5Cxi_%7B2%7D%7D%20%2C%5Ccdots%20%2C%5Cvec%7B%5Cxi_%7Bn%7D%7D%0A%5Cend%7Bbmatrix%7D$ 看作系数矩阵， $%5Cvec%7Bk%7D%20%3D%5Cbegin%7Bbmatrix%7D%0A%20k_%7B1%7D%20%26%20k_%7B2%7D%20%26%20%5Ccdots%20%26%20k_%7Bn%7D%0A%5Cend%7Bbmatrix%7D%5E%7BT%7D$ 看作变量，其中 m 为某一季节应季农作物的种类数，n 为基础解系中包含特解的个数，那么原方程组的通解其实是一个非齐次线性方程组，即 $%5Cbegin%7Bbmatrix%7D%0A%20%5Cvec%7B%5Cxi_%7B2%7D%7D%20%2C%5Cvec%7B%5Cxi_%7B2%7D%7D%20%2C%5Ccdots%20%2C%5Cvec%7B%5Cxi_%7Bn%7D%7D%0A%5Cend%7Bbmatrix%7D%20%5Cvec%7Bk%7D%20%3D%5Cvec%7Bx%7D%20$ ，展开之后可得

$%5Cbegin%7Bbmatrix%7D%20%20%0A%20%20%5Cxi_%7B11%7D%26%20%5Cxi_%7B21%7D%26%20%5Ccdots%20%20%26%20%5Cxi_%7Bn1%7D%20%5C%5C%20%20%0A%20%20%5Cxi_%7B12%7D%26%20%5Cxi_%7B22%7D%26%20%5Ccdots%20%20%26%20%5Cxi_%7Bn2%7D%20%5C%5C%20%20%0A%20%20%5Cvdots%20%26%20%5Cvdots%20%26%20%5Cddots%20%26%20%5Cvdots%20%5C%5C%20%20%0A%20%20%5Cxi_%7B1m%7D%26%20%5Cxi_%7B2m%7D%26%20%5Ccdots%20%20%26%20%5Cxi_%7Bnm%7D%20%20%0A%5Cend%7Bbmatrix%7D%20%20%0A%5Cbegin%7Bbmatrix%7D%0A%20k_%7B1%7D%20%5C%5C%0A%20k_%7B2%7D%20%5C%5C%0A%20%5Cvdots%20%5C%5C%0A%20k_%7Bn%7D%0A%5Cend%7Bbmatrix%7D%0A%3D%5Cbegin%7Bbmatrix%7D%0A%20x_%7B1%7D%20%5C%5C%0A%20x_%7B2%7D%20%5C%5C%0A%20%5Cvdots%20%5C%5C%0A%20x_%7Bm%7D%0A%5Cend%7Bbmatrix%7D$ （3）

如果能够知道一组 $%5Cvec%7Bx%7D%20$ 的值或了解 $%5Cvec%7Bx%7D%20$ 的限定条件，便可以反解出 $%5Cvec%7Bk%7D$ 。根据饥荒联机版种植系统的游戏规则， $%5Cvec%7Bx%7D%20$ 需要满足以下限定条件：

要想农作物的养分能够自给自足，一块耕地上至少种植2棵农作物，即 $%5Csum_%7Bi%3D1%7D%5Em%20x_%7Bi%7D%20%5Cgeq%202$ ；
一块耕地上种植的农作物超过10棵会被判定为拥挤，增加农作物的压力值，因此一块耕地上种植的农作物不得超过10棵，即 $%5Csum_%7Bi%3D1%7D%5Em%20x_%7Bi%7D%20%5Cleq%2010$ ；
每个季节每种农作物种植的数量不能为负数，即 $x_%7Bi%7D%20%5Cgeq%200%EF%BC%8Ci%3D1%2C2%2C%5Ccdots%20%2Cm$

对于条件3，由于 $A%5Cvec%7Bx%7D%20%3D%5Cvec%7B0%7D$ 是一个齐次方程组，因此基础解系 $%5Cbegin%7Bbmatrix%7D%0A%20%5Cvec%7B%5Cxi_%7B2%7D%7D%20%2C%5Cvec%7B%5Cxi_%7B2%7D%7D%20%2C%5Ccdots%20%2C%5Cvec%7B%5Cxi_%7Bn%7D%7D%0A%5Cend%7Bbmatrix%7D$ 中一定包含一个 n 阶的单位矩阵 $E$ ，即基础解系可以写成 $%5Cbegin%7Bbmatrix%7D%0AB_%7Bn%5Ctimes%20(m-r)%7D%20%5Cmid%20%20E_%7Bn%5Ctimes%20%20n%7D%5C%5C%0A%5Cend%7Bbmatrix%7D%5E%7BT%7D$ 的分块矩阵的形式，其中 r 为基础解系的秩。比如，冬天农作物求得的基础解系为 $%5Cbegin%7Bbmatrix%7D%20%20-2%20%26%201%5C%5C%20%200%20%26%201%5C%5C%20%201%20%26%200%5C%5C%20%200%20%26%201%20%5Cend%7Bbmatrix%7D$ ，最后两行刚好为单位矩阵 $%5Cbegin%7Bbmatrix%7D%0A%201%20%26%200%5C%5C%0A%200%20%26%201%0A%5Cend%7Bbmatrix%7D$ 。又因为

$E%5Cvec%7Bk%7D%3D%5Cvec%7Bk%7D%3D%5Cbegin%7Bbmatrix%7D%20%20k_1%20%5C%5C%20%20k_2%20%5C%5C%20%20%5Cvdots%20%5C%5C%20%20k_n%20%5Cend%7Bbmatrix%7D%20%3D%5Cbegin%7Bbmatrix%7D%20%20x_%7Bm-n%2B1%7D%20%5C%5C%20%20x_%7Bm-n%2B2%7D%20%5C%5C%20%20%5Cvdots%20%5C%5C%20%20x_m%20%5Cend%7Bbmatrix%7D$

所以 $x_%7Bi%7D%20%5Cgeq%200$ 可以推导出 $k_%7Bi%7D%20%5Cgeq%200%EF%BC%8Ci%3D1%2C2%2C%5Ccdots%20%2Cn$ 。将单位矩阵这一部分单独看成一个限定条件，于是限定条件可以整理成如下标准形式：

$%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%0A%5Csum_%7Bi%3D1%7D%5Em%20-x_%7Bi%7D%20%5Cleq%20-2%20%5C%5C%0A%5Csum_%7Bi%3D1%7D%5Em%20x_%7Bi%7D%20%5Cleq%2010%5C%5C%0A-B_%7Bn%5Ctimes%20r%7D%5E%7BT%7D%5Cvec%7Bk%7D%20%5Cleq%200%20%5C%5C%0Ak_%7Bi%7D%20%5Cgeq%200%2Ci%3D1%2C2%2C%5Ccdots%20%2Cn%0A%5Cend%7Bmatrix%7D%5Cright.$ （4）

这是一个关于 $%5Cvec%7Bk%7D%20$ 的线性不等式组，找出其所有的整数解，问题就可解决。然而，不等式组是没有通用公式可以求解的。因此接下来，仍以冬天为例，介绍一组不等式组的求解方法。

将基础解系 $%5Cbegin%7Bbmatrix%7D%0A%20-2%20%26%201%5C%5C%0A%200%20%26%201%5C%5C%0A%201%20%26%200%5C%5C%0A%200%20%26%201%0A%5Cend%7Bbmatrix%7D$ 代入到不等式组（4），展开可得

$%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%0A-x_1-x_2-x_3-x_4%5Cle%20-2%20%5C%5C%0Ax_1%2Bx_2%2Bx_3%2Bx_4%5Cle%2010%20%5C%5C%0A2k_1-k_2%5Cle%200%20%5C%5C%0A-k_2%5Cle%200%20%5C%5C%0Ak_%7Bi%7D%20%5Cgeq%200%2Ci%3D1%2C2%0A%5Cend%7Bmatrix%7D%5Cright.$

进一步展开可得

$%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%0Ak_1-3k_2%5Cle%20-2%20%5C%5C%0A-k_1%2B3k_2%5Cle%2010%20%5C%5C%0A2k_1-k_2%5Cle%200%20%5C%5C%0A-k_2%5Cle%200%20%5C%5C%0Ak_%7Bi%7D%20%5Cgeq%200%2Ci%3D1%2C2%0A%5Cend%7Bmatrix%7D%5Cright.$ （5）

要求出不等式组（5）的自然数解，先看这样一个例子，假如要求解 $x_1%2B2x_2%5Cleq%2010$ ，既然 $x_1%2B2x_2$ 比10小，所以可以再补上一个非负数 $x_3$ ，使之刚好等于10，即 $x_1%2B2x_2%2Bx_3%3D%2010$ ，这样一来，就把不等式改写成了等式方程。借助这个思想，可以构造出如下线性方程组

$%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%0A%5Cbegin%7Balign*%7D%0A%20k_1-3k_2%2Bk_3%3D%20-2%20%5C%5C%0A%20-k_1%2B3k_2%2Bk_4%3D%2010%20%5C%5C%0A%202k_1-k_2%2Bk_5%3D%200%20%5C%5C%0A%20-k_2%2Bk_6%3D%200%20%20%5C%5C%0A%5Cend%7Balign*%7D%5C%5C%0A%5Cend%7Bmatrix%7D%5Cright.%2C%0A%20k_%7Bi%7D%20%5Cgeq%200%2Ci%3D1%2C2%2C%5Ccdots%20%2C6$ （6）

这种做法的实质是，在不等式组（5）的系数矩阵右侧串联了一个 m 阶的单位矩阵，也就是说，最终构造的用于求解 $%5Cvec%7Bk%7D%20$ 的系数矩阵的方式如下

先定义如下几个运算：

设基础解系 $Y%3D%5Cbegin%7Bbmatrix%7D%0A%20%5Cvec%7B%5Cxi_%7B2%7D%7D%20%2C%5Cvec%7B%5Cxi_%7B2%7D%7D%20%2C%5Ccdots%20%2C%5Cvec%7B%5Cxi_%7Bn%7D%7D%0A%5Cend%7Bbmatrix%7D$ ，最终构造的用于求解 $%5Cvec%7Bk%7D%20$ 的系数矩阵 $C$ 为

$C%3D%5Cbegin%7Bbmatrix%7D%0A%20%5Cbegin%7Bbmatrix%7D%0A%20-S_%7Bcol%7D(Y)%20%5C%5C%0A%20S_%7Bcol%7D(Y)%20%5C%5C%0A%20Y%5E%7B%5B1%5Csim%20m-r%2C*%5D%7D%0A%5Cend%7Bbmatrix%7D%2C%20E_%7B(2%2Bm-r)%5Ctimes%20(2%2Bm-r)%7D%0A%5Cend%7Bbmatrix%7D$

其中，m 仍为自变量的个数，也就是某一季节应季农作物的种类数，r 仍为基础解系 $Y$ 的秩， $E$ 为 2+m-r 阶的单位矩阵。

之后，便可以建立最终的求解 k 的方程组

$C%5Cvec%7Bk%7D%3D%5B-2%20%5Cquad%2010%20%5Cquad%20%5Cunderbrace%7B0%5Ccdots0%7D_%7Br%E4%B8%AA0%7D%5D%5ET$

接下来要做的就是求解这个关于 $%5Cvec%7Bk%7D%20$ 的方程组。将这一非齐次线性方程组套用方法一中的5个步骤，即可求得所有满足条件的 $%5Cvec%7Bk%7D%20$ 。

对于方程组（6）而言，一共求得5个满足条件的 $%5Cvec%7Bk%7D%20$ ，分别是

$%5Cbegin%7Bmatrix%7D%0A%20%5Cvec%7Bk_1%5E%7B'%7D%7D%20%3D%5Cbegin%7Bbmatrix%7D%0A%200%20%26%200%20%26%201%20%26%205%20%26%200%20%26%200%0A%5Cend%7Bbmatrix%7D%5ET%20%5C%5C%0A%20%5Cvec%7Bk_2%5E%7B'%7D%7D%20%3D%5Cbegin%7Bbmatrix%7D%0A%201%20%26%202%20%26%206%20%26%200%20%26%200%20%26%202%0A%5Cend%7Bbmatrix%7D%5ET%20%5C%5C%0A%20%5Cvec%7Bk_3%5E%7B'%7D%7D%20%3D%5Cbegin%7Bbmatrix%7D%0A%200%20%26%200%20%26%201%20%26%205%20%26%200%20%26%200%0A%5Cend%7Bbmatrix%7D%5ET%20%5C%5C%0A%20%5Cvec%7Bk_4%5E%7B'%7D%7D%20%3D%5Cbegin%7Bbmatrix%7D%0A%200%20%26%200%20%26%201%20%26%205%20%26%200%20%26%200%0A%5Cend%7Bbmatrix%7D%5ET%20%5C%5C%0A%5Cvec%7Bk_5%5E%7B'%7D%7D%20%3D%5Cbegin%7Bbmatrix%7D%0A%200%20%26%205%20%26%208%20%26%2018%20%26%205%20%26%205%0A%5Cend%7Bbmatrix%7D%5ET%20%0A%5Cend%7Bmatrix%7D$

但是因为 $k_3%2Ck_4%2Ck_5%2Ck_6$ 是为了求解不等式组而人为增加的变量，没有实际意义，因此需要将每个解向量中的后四个元素删除，删除之后，再次化简，仍然符合条件的解向量还剩下两个，分别是

$%5Cvec%7Bk_1%7D%20%3D%5Cbegin%7Bbmatrix%7D%0A%201%20%5C%5C%0A%202%0A%5Cend%7Bbmatrix%7D%2C%0A%5Cvec%7Bk_2%7D%20%3D%5Cbegin%7Bbmatrix%7D%0A%200%20%5C%5C%0A%201%0A%5Cend%7Bbmatrix%7D$

将这两个值代入到式（2），可以得到2个基本可行解，分别是

$%5Cbegin%7Bmatrix%7D%0A%20%5Cvec%7Bx_1%7D%20%3D1%5Cbegin%7Bbmatrix%7D%0A%20-2%20%5C%5C%0A%200%20%5C%5C%0A%201%20%5C%5C%0A%200%0A%5Cend%7Bbmatrix%7D%0A%2B2%5Cbegin%7Bbmatrix%7D%0A%201%20%5C%5C%0A%201%20%5C%5C%0A%200%20%5C%5C%0A%201%0A%5Cend%7Bbmatrix%7D%0A%3D%5Cbegin%7Bbmatrix%7D%0A%200%20%5C%5C%0A%202%20%5C%5C%0A%201%20%5C%5C%0A%202%0A%5Cend%7Bbmatrix%7D%20%5C%5C%0A%5Cvec%7Bx_2%7D%20%3D0%5Cbegin%7Bbmatrix%7D%0A%20-2%20%5C%5C%0A%200%20%5C%5C%0A%201%20%5C%5C%0A%200%0A%5Cend%7Bbmatrix%7D%0A%2B1%5Cbegin%7Bbmatrix%7D%0A%201%20%5C%5C%0A%201%20%5C%5C%0A%200%20%5C%5C%0A%201%0A%5Cend%7Bbmatrix%7D%0A%3D%5Cbegin%7Bbmatrix%7D%0A%201%20%5C%5C%0A%201%20%5C%5C%0A%200%20%5C%5C%0A%201%0A%5Cend%7Bbmatrix%7D%20%0A%5Cend%7Bmatrix%7D$

每一个基本可行解都对应了一种具体的搭配方案，这两种搭配方案分别是：

胡萝卜植株/南瓜植株：大蒜植株：土豆植株 = 2：1：2

芦笋蕨：胡萝卜植株/南瓜植株：土豆植株 = 1：1：1

这就是冬天的全部的2种搭配方案，大家可以自行验证。将四个季节都按照这种方法计算，即可得到所有的搭配方案。

！！前方高能！！

三、计算结论

接下来就是本文最最最重点的地方啦！以下就是求出的所有农作物搭配方案。

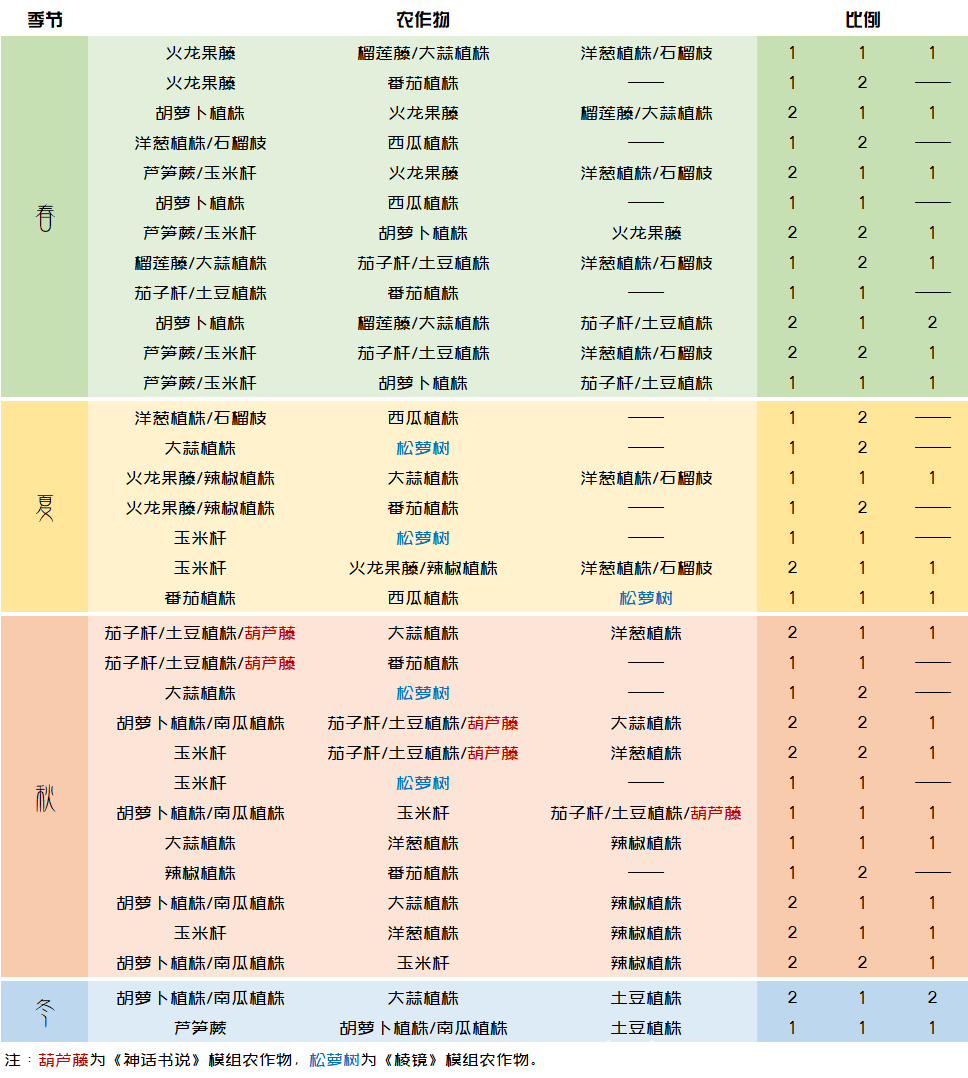
其中，春天共有12种搭配方案，夏天共有4种搭配方案，秋天共有10种搭配方案，春天共有2种搭配方案。

以上求得的搭配方案是一个极大线性无关组，也就是说，通过以上搭配方案无法推导出表中已给出的任何一个搭配方案。但是，将以上搭配方案进行任意线性组合，就可以得到任意一种新的搭配方案。例如，在春天，已知：

榴莲藤/大蒜植株：茄子杆/土豆植株：洋葱植株/石榴枝 = 1：2：1

胡萝卜植株：榴莲藤/大蒜植株：茄子杆/土豆植株 = 2：1：2

将两个比例相加，就可以推导出

茄子杆/土豆植株：胡萝卜植株：榴莲藤/大蒜植株：洋葱植株/石榴枝 = 4：2：2：1

也可以是一种比例的倍数加上另一种比例的倍数，比如，在春天，已知

胡萝卜植株：西瓜植株 = 1：1

洋葱植株/石榴枝：西瓜植株 = 1：2

将第一个搭配的3倍加上第二个搭配的1倍，就可以推导出：

洋葱植株/石榴枝：胡萝卜植株：西瓜植株 = 1：3：5

那么，接下来，本文就在充分考虑耕地种得下、不拥挤、能形成家族的基础上，对常见的由线性组合而派生出的搭配做一个补充，用来给闲着没事爱折腾的玩家一个参考，但是实用性不强，不如上面给出的那些基本组合。

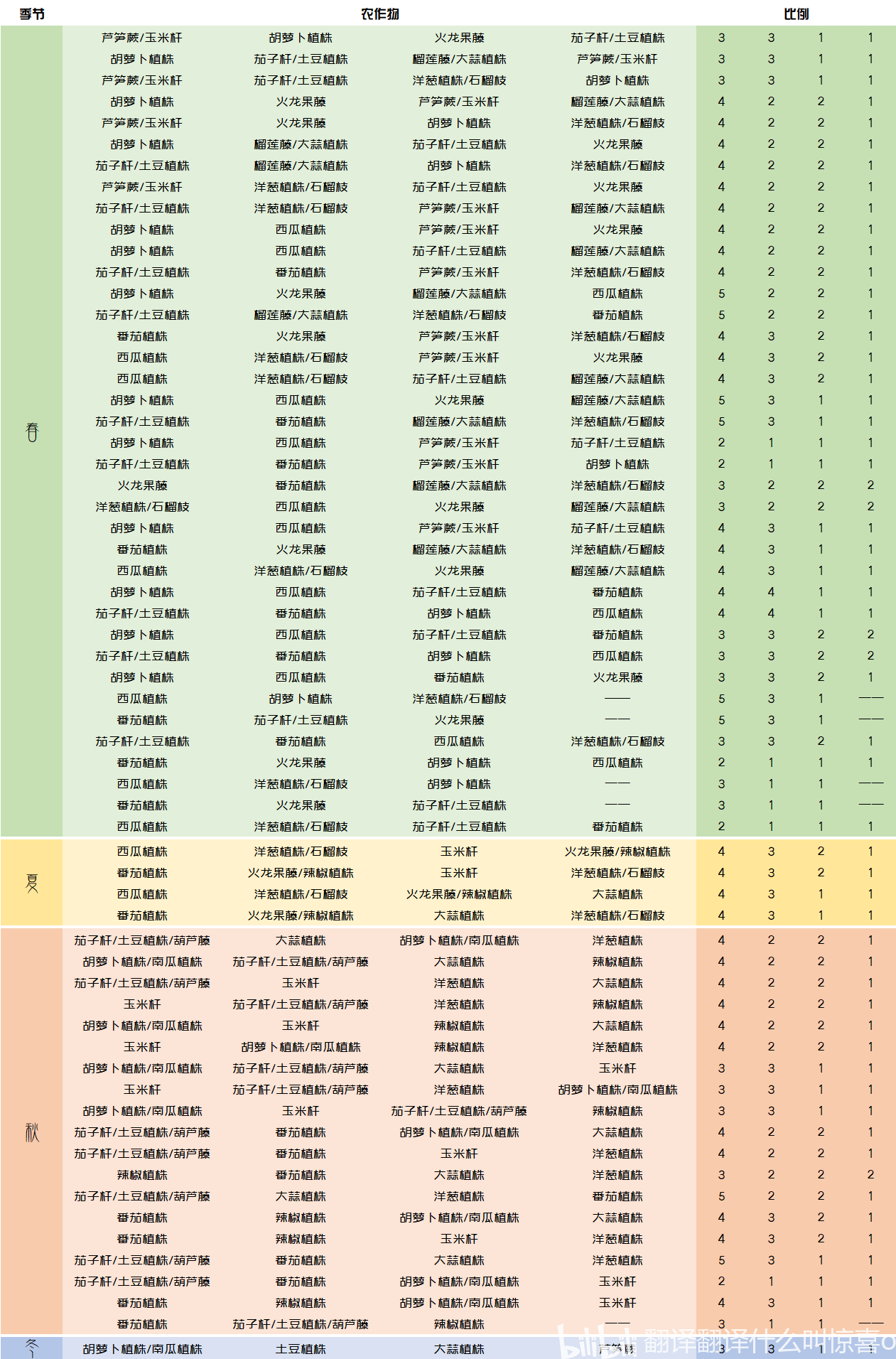
总之，方程组有无穷多解，也就意味着如果不考虑耕地限制的话，有无穷多种合理的搭配方案，但是我们只需要求出一个解的极大线性无关组，根据自己的种植需要合理地进行线性组合即可。如果自己推导出的新组合无法同时达成 “不拥挤” 和 “形成家族” 两个条件，那么就无法种植出巨大农作物，但是不影响养分的自给自足，依然可以不用施肥。

四、结论的应用——农作物搭配建议

在耕地之前，建议订阅一个模组，名为Snapping tills，可以帮助整齐地耕地。

这里推荐几种非常优秀的搭配方案。

· 搭配方案一

胡萝卜植株：大蒜植株：土豆植株 = 2：1：2

适用季节：【春】【秋】【冬】

推荐理由：

此方案只有夏天不能种植。
使用【1大蒜+2土豆+1胡萝卜】可以在烹饪锅中制作出奶油土豆泥，回复37.5饱食度、33精神、20血量，是少有的回复精神较多的食物，关键是原料全部可以实现量产。
土豆直接烤熟了吃就可以回复25饱食度和20血量，仅一个烹饪锅中的土豆如果直接烤熟了吃，就可以恢复100饱食度和80血量，几个烤土豆下肚直接大补。
胡萝卜是一种优秀的蔬菜类填充物，具有1蔬菜度。
胡萝卜可以用来雇佣兔人。
胡萝卜和土豆在神话书说模组中都可用于烹饪素斋，回复75饱食度。

这一搭配受季节限制小，功能非常全面，是除了火龙果之外个人最为推荐的一种搭配方案。

种植示范：

· 搭配方案二

土豆植株：番茄植株 = 1：1

适用季节：【春】【秋】

推荐理由：

大力士必备。土豆直接烤熟了吃就可以回复25饱食度和20血量，沃尔夫冈食用烤土豆可以回复40饱食度和20血量。
使用【3番茄+1冰】可以烹饪出蔬菜鸡尾酒，回复25饱食度、33精神、3血量，是良好的回复精神的食物。
1：1的方案可以在一块耕地中培育出5个巨大土豆和5个巨大番茄，对单一农作物而言产量非常高。
番茄是一种蔬菜类填充物，具有1蔬菜度，烤蕃茄可以回复12.5饱食度和20血量。
秋天时大厨沃利玩家可以将本方案与<搭配方案四>一起种植，同时收获多种关键的农作物食材。
在神话书说模组中，这两种农作物都可以作为素斋的烹饪原料。类似的搭配还有春天的胡萝卜+西瓜1：1组合。

吃饱就行，谁愿意管理这么多种类的农作物的果实和种子啊

种植示范：

· 搭配方案三

火龙果藤：番茄植株 = 1：2

适用季节：【春】【夏】

推荐理由：

在这一搭配下，【任意数量火龙果+任意数量番茄】即可烹饪出火龙果派，回复75饱食度、5精神和40血量。
火龙果派不仅回复效果显著，而且食用前摇和后摇都很短，无论是用来日常充饥还是在战斗中快速回血，都是一种很不错的选择。
使用【3番茄+1冰】可以烹饪出蔬菜鸡尾酒，回复25饱食度、33精神、3血量，是良好的回复精神的食物。若将火龙果派和蔬菜鸡尾酒搭配食用可以获得可观的三维回复。

火龙果堪称水果中的极品，一般来讲，春天夏天必种植火龙果。

种植示范：

· 搭配方案四

大蒜植株：辣椒植株：洋葱植株 = 1：1：1

适用季节：【夏】【秋】

推荐理由：

大厨沃利必备。沃利可以使用便携研磨器将大蒜加工成蒜粉，为料理提供33%减伤效果，还可以将辣椒加工成辣椒面，为料理提供20%的伤害加成。
洋葱是制作骨头汤、海鲜杂烩、恐怖国王饼的必备原料。
在夏天也可以将任意数量的洋葱换成石榴（注意家族），石榴具有1水果度，烤石榴可以恢复20生命值。
秋天时沃利玩家可以将本方案与<搭配方案二>一起种植，同时收获多种关键的农作物食材。

种植示范：

· 搭配方案五

大蒜植株：洋葱植株：番茄植株：辣椒植株 = 2：2：2：3

适用季节：【夏】【秋】

推荐理由：

方案四的进阶版本，大厨沃利必备。大蒜和辣椒可以为沃利提供蒜粉和辣椒粉的来源，为料理增加BUFF。
沃利专属料理海鲜杂烩可以回复112.5饱食度、33精神和60血量，其原料需要【洋葱+番茄+鱼+填充物】，可以直接用洋葱、番茄或鱼充当填充物，本方案可以一次性满足所有的农作物类原料。
【洋葱+番茄+填充物】可以烹饪出生鲜萨尔萨酱，【3番茄+1冰】可以烹饪出蔬菜鸡尾酒，这两种料理都可以回复25饥饿、33精神和3血量，是良好的回复精神的食物。
在夏天可以将下图中连续的4个洋葱换成4个石榴，石榴具有1水果度，烤蕃茄和烤石榴都可以回复20血量。

种植示范：

其余的搭配方案虽然没有在这里推荐，但不代表没有用处，大家可以根据自己的需要，灵活调整种植计划。另外别忘了，不同的搭配方案是可以在同一块耕地中混用的，这一点在前期扩大种子储备、保证农作物种子的多样性是很重要的。

三连，三连，重要的三连说三遍 ^o^

【饥荒联机版】巨大农作物种植搭配技巧——生活处处离不开数学 - 哔哩哔哩

前言

一、农作物基本情况介绍

二、线性模型的建立与求解

三、计算结论

四、结论的应用——农作物搭配建议