机会成本与会计成本

==会计成本== 也叫“直接成本”或"显成本"。 会计成本是指实际支付的货币成本。

三种类型： 1.费用 2.资产 3.损失

==机会成本== 机会成本是指在面临多方案择一决策时，被舍弃的选项中的最高价值者是本次决策的机会成本。

只有超过一个以上选择时才有机会成本。

显性成本和隐性成本

==显性成本== 显性成本是指计入账内的、看得见的实际支出，例如支付的生产费用、工资费用、市场营销费用等，因而它是有形的成本。也叫会计成本。

==隐性成本== 隐性成本是相对于显性成本而言，是一种隐藏于经济组织总成本之中、游离于财务监督之外的成本。

总成本或经济成本

显性成本 + 隐性成本 = 总成本

经济利润、会计利润、正常利润

会计利润 = 经济利润 + 隐性成本 正常利润是隐性成本的一部分 正常利润（Normal profits）是一个人留在一个行业最小的报酬。

上市公司公布的是会计利润。

增量成本与沉末成本

==沉没成本==已经花掉的钱再也回不来了，对以后的决策不起作用的成本。

沉没成本是指已发生或承诺、无法回收的成本支出，如因失误造成的不可收回的投资。沉没成本是一种历史成本，对现有决策而言是不可控成本，不会影响当前行为或未来决策。从这个意义上说，在投资决策时理性的决策者应排除沉没成本的干扰。

==增量成本==是指与价格以及销售量的变动紧密相关的那些成本，等于生产增量之后的总成本减去生产增量前的总成本。

边际成本

边际成本是指厂商每增加一单位产量所增加的成本。

短期成本函数

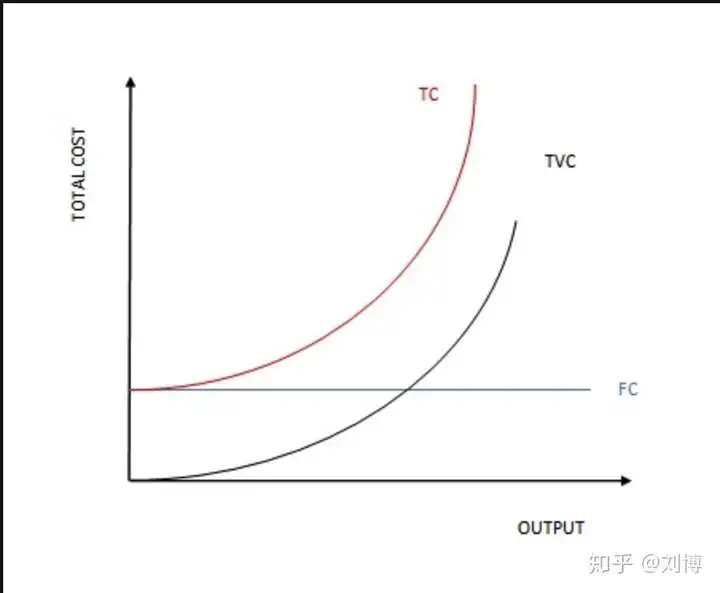
TFC是总固定成本（图中是FC）

TVC是总可变成本

TC是总成本 = TFC + TVC

AFC 是平均固定成本

AVC 是平均变动成本

AC（ATC） 是平均总成本

MC 是边际成本，是总成本的一阶导数

总成本的一阶导数是边际成本，求总成本的最小值，就是求一节导数为0，二阶导数为正，由于边际成本是递增的（也就是二阶导数为正），因此不违背数学原理。

长期平均成本曲线LAC

如果LAC呈U型，如下：

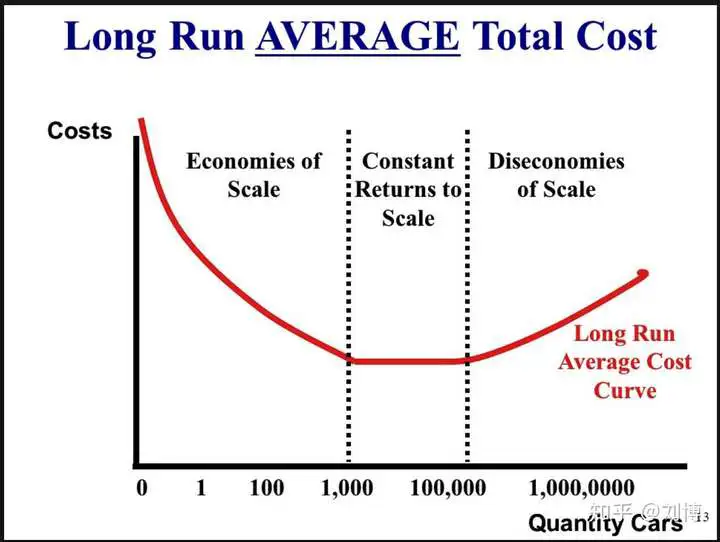
Economies of Scale：规模经济，此时规模报酬递增 Constant Returns to Scale：规模报酬不变 Diseconomies of Scale：规模不经济，此时规模报酬递减

由于企业内部带来的成本下降叫做内在规模经济。 由于企业外部、整个行业技术进步带来的成本下降叫做外在规模经济。

盈亏平衡分析

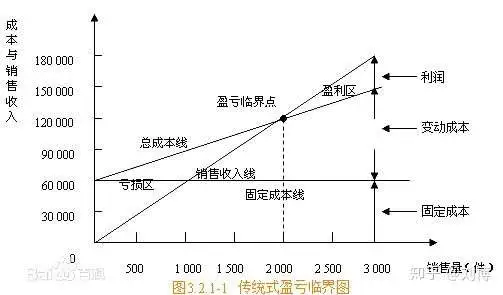
==盈亏平衡点（Break Even Point,简称BEP）==通常是指全部销售收入 等于全部成本时（销售收入线与总成本线的交点）的产量。以盈亏平衡点的界限，当销售收入高于盈亏平衡点时企业盈利，反之，企业就亏损。盈亏平衡点可以用销售量来表示，即盈亏平衡点的销售量；也可以用销售额来表示，即盈亏平衡点的销售额。

==安全边际===现有 (预计未来可以实现的) 销售量-盈亏两平销售量。

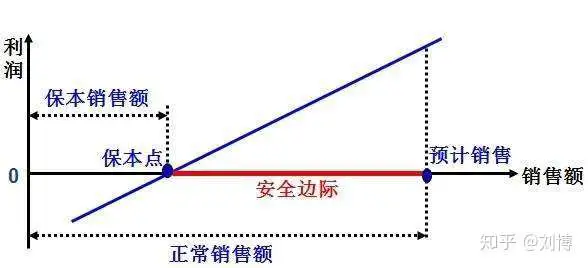
==安全边际率===安全边际÷现有 (预计未来可以实现的) 销售量

==经营杠杆率DOL==（Degree of Operating Leverage，DOL）又叫做经营风险，是息税前利润的变动率相当于销售额（营业额）变动率的倍数。

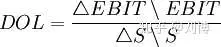
DOL ---- 营业杠杆系数； EBIT ---- 营业利润，即息税前利润； △EBIT ---- 营业利润的变动额； S ---- 营业额； △S ---- 营业额的变动额。

市场结构论

==划分== 粗划分：完全竞争市场和不完全竞争市场

市场结构可细分为4种类型： 1. 完全竞争 2. 完全垄断 3. 垄断竞争 4. 寡头垄断

==判断== 判断标准：厂商的数量、产品的性质、厂商对价格的控制程度、进入市场的难易程度。

==完全竞争市场的需求曲线==

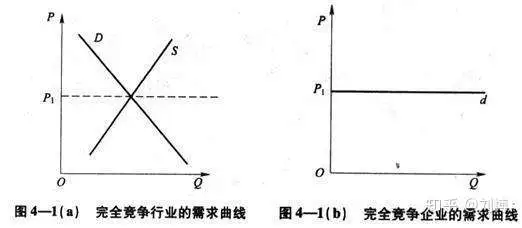
在完全竞争市场单个厂商是价格接受者。

==完全竞争市场的收益曲线==

完全竞争市场AR = MR = P

收益TR（图中是R）=P * Q

==完全竞争市场如何求利润极大化== 设π为利润，Q为厂商产量，TR为厂商总收益，TC为厂商总成本，则

π(Q) = TR(Q) − TC(Q)

利润极大化的必要条件是π对Q的一阶导数为零，而TR对Q的一阶导数就是边际收益MR，同样，TC对Q的一节导数就是边际成本MC。所以，当MR=MC，即边际收益等于边际成本时，利润极大，即：

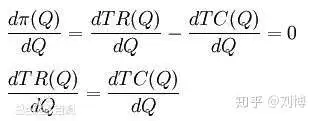
即MR = MC

利润最大化的充分条件还要求π的二阶导数为负数（数学上二阶导数<0即凸函数），它表示，利润最大化要求边际成本函数的斜率要大于边际收益函数的斜率。

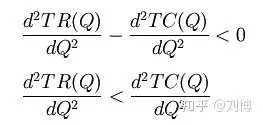
==完全竞争市场短期均衡的各种条件==

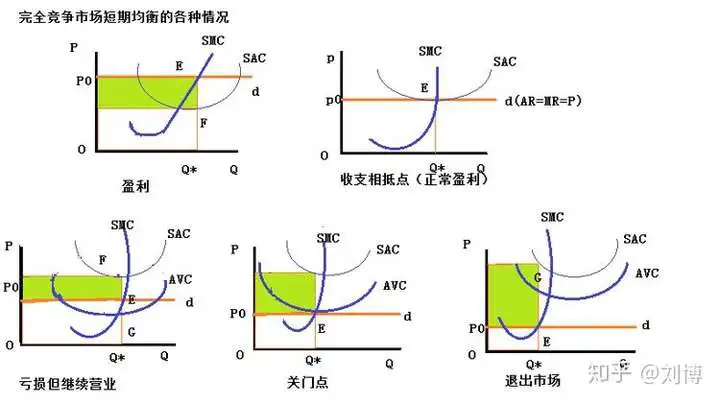
完全竞争市场长期均衡时，利润一定为0。

节俭悖论

“节约悖论（Paradox of thrift）”是凯恩斯推广的而流行的一种理论，虽然一直说早在1714年在蜜蜂的寓言，和类似的情绪可以追溯到古代，根据凯恩斯主义的国民收入决定理论，消费的变动会引起国民收入同方向变动，储蓄的变动会引起国民收入反方向变动。但根据储蓄变动引起国民收入反方向变动的理论，增加储蓄会减少国民收入，使经济衰退，是恶的；而减少储蓄会增加国民收入，使经济繁荣，是好的，这种矛盾被称为"节约悖论"。

什么是博弈

行为主体选择策略并相互影响的过程。

双人零和博弈

零和博弈是博弈论的一个概念，属非合作博弈，指参与博弈的双方，在严格竞争下，一方的收益必然意味着另一方的损失，博弈各方的收益和损失相加的总和永远为“零”。

博弈的构成要素

1. 参与人(players)：做决策的个体
2. 行动(actions)或策略(strategies)：所能做的某一选择
3. 信息(infomation)：参与人的特征
4. 收益(payoffs)
5. 均衡(equilibria)或结果(outcome)

博弈分类

同时行动叫静态博弈，先后行动叫动态博弈。

纳什均衡

纳什均衡，又称为非合作博弈均衡，是博弈论的一个重要术语，以约翰·纳什命名。在一个博弈过程中，无论对方的策略选择如何，当事人一方都会选择某个确定的策略，则该策略被称作支配性策略。如果两个博弈的当事人的策略组合分别构成各自的支配性策略，那么这个组合就被定义为纳什均衡。

囚徒困境

囚徒困境属于完全信息静态博弈。 个人的理性选择导致了集体的非理性结果。 纳什均衡的结果是两人都坦白。

情侣博弈

属于完全信息静态博弈。

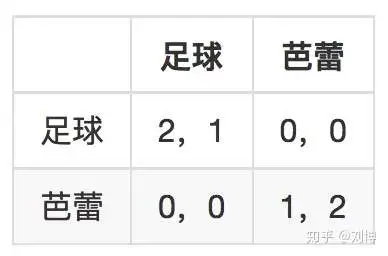
此博弈有两个纳什均衡，同时看芭蕾或足球。 此时话语权的争夺特别重要。

斗鸡博弈

斗鸡博弈(Chicken Game)其实是一种误译。Chicken在美国口语中是“懦夫”之意，Chicken Game本应译成懦夫博弈。

试想有两人狭路相逢，每人有两个行动选择：一是退下来，一是进攻。如果一方退下来，而对方没有退下来，对方获得胜利，这人就很丢面子；如果对方也退下来，双方则打个平手；如果自己没退下来，而对方退下来，自己则胜利，对方则失败；如果两人都前进，那么则两败俱伤。因此，对每个人来说，最好的结果是，对方退下来，而自己不退。

纳什均衡有两个，两个一进一退。

关键在于判断对方的决策是否为真。

博弈树

博弈树是指由于动态博弈参与者的行动有先后次序，因此可以依次将参与者的行动展开成一个树状图形。

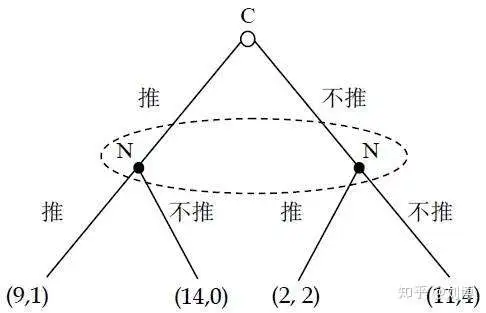
子博弈精炼纳什均衡

子博弈:一个扩展式表示博弈的子博弈G是由一个单结信息集x开始的与所有该决策结的后续结(包括终点结)组成的能自成一个博弈的原博弈的一部分。

对于扩展式博弈的策略组合S=(S1,…,Si,…,Sn),如果它是原博弈的纳什均衡;它在每一个子博弈上也都构成纳什均衡,则它是一个子博弈精炼纳什均衡。

相关链接

承诺行动就是让威胁可信的行动。

智猪博弈

在博弈论（Game Theory）经济学中，“智猪博弈”是一个著名的纳什均衡的例子。假设猪圈里有两头猪，一头大猪，一头小猪。

猪圈很长，一头有一踏板，另一头是饲料的出口和食槽。猪每踩一下踏板，另一边就会有相当于10份的猪食进槽，但是踩踏板以后跑到食槽所需要付出的“劳动”，加起来要消耗相当于2份的猪食。

问题是踏板和食槽分置笼子的两端，如果有一只猪去踩踏板，另一只猪就有机会抢先吃到另一边落下的食物。踩踏板的猪付出劳动跑到食槽的时候，坐享其成的另一头猪早已吃了不少。

“笼中猪”博弈的具体情况如下：如果两只猪同时踩踏板，同时跑向食槽，大猪吃进7份，得益5份，小猪吃进3份，实得1份；如果大猪踩踏板后跑向食槽，这时小猪抢先，吃进4份，实得4份，大猪吃进6份，付出2份，得益4份；如果大猪等待，小猪踩踏板，大猪先吃，吃进9份，得益9份，小猪吃进1份，但是付出了2份，实得-1份；如果双方都懒得动，所得都是0。

利益分配格局决定两头猪的理性选择：小猪踩踏板只能吃到一份，不踩踏板反而能吃上4份。对小猪而言，无论大猪是否踩动踏板，小猪将选择“搭便车”策略，也就是舒舒服服地等在食槽边，这是最好的选择。

现在来看大猪。由于小猪有“等待”这个优势策略，大猪只剩下了两个选择：等待，一份也得不到；踩踏板得到4份。所以“等待”就变成了大猪的劣势策略，当大猪知道小猪是不会去踩动踏板的，自己亲自去踩踏板总比不踩强吧，只好为一点残羹不知疲倦地奔忙于踏板和食槽之间。

现实中的智猪博弈：大企业做研发，小企业做山寨