一、基本概念
- 领域:与某像素相邻的像素的聚合。3x3、5x5领域等,类比卷积核。
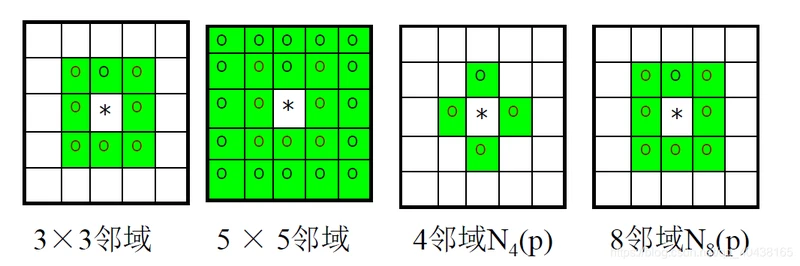
- 层次:表示图像实际拥有的灰度级的数量。灰度级越高越好,即图像深度越深越好。8比特深度对应256灰度级,图像有256个层次。
- 对比度:灰度反差大小。最大灰度值/最小灰度值。
- 清晰度:跟亮度、对比度、层次大小、细微层次和颜色饱和度有关。
- 图像处理内容包括:图像增强(去雾)、图像恢复、图像重建、图像分割、图像压缩、图像识别、图像跟踪。
二、图像空域滤波
\quad
定义(2a+1)*(2b+1)模板/滤波器/核为
w
(
i
,
j
)
(
−
a
≤
i
≤
a
,
−
b
≤
j
≤
b
)
w(i,j)(-a \le i \le a, -b \le j \le b)
w(i,j)(−a≤i≤a,−b≤j≤b),则对于图中任意一个像素点
f
(
x
,
y
)
f(x,y)
f(x,y),则经过核处理后为:
g
(
x
,
y
)
=
∑
s
=
−
a
a
∑
t
=
−
b
b
w
(
s
,
t
)
f
(
x
+
s
,
y
+
t
)
g(x, y) = \sum_{s=-a}^a \sum_{t=-b}^b w(s,t)f(x+s,y+t)
g(x,y)=s=−a∑at=−b∑bw(s,t)f(x+s,y+t)
这步运算也称为卷积运算或者相关运算。
设核尺寸为mxn则:
- 原图扩充m-1行,n-1列
- 模板置于初始位置与覆盖图像区域对应点相乘并求和;
- 循环遍历整个数据;
- 剪切开始填充的数据,保留与原始图像相同的区域;
- 结束。
1、平滑滤波器
作用:模糊处理,去除图像中一些不重要的细节、减小噪声
类别:均值滤波器、最大值滤波器、中值滤波器等
2、局部平均法
原理:用当前像素邻域内像素平均灰度值代替当前像素的原灰度值。
1、简单平均法

- 平滑后图像噪声变为原来的 1 M \frac{1}{M} M1,M为滤波器大小m*n
- 简单局部平均会使图像模糊,特别是轮廓边缘不清晰
2、阈值平均法
\quad
仅当平滑前后图像差值大于某个预先给定的值时,实施简单局部平均,即:
G
‾
(
x
,
y
)
=
{
g
‾
(
x
,
y
)
当
∣
g
(
x
,
y
)
−
g
‾
(
x
,
y
)
∣
>
T
时
}
\overline{G}(x,y)=\{\overline{g}(x,y) \quad当|g(x,y)-\overline{g}(x,y)|>T时\}
G(x,y)={g(x,y)当∣g(x,y)−g(x,y)∣>T时}
T为预先设定的阈值。
- 该方法对抑制椒盐噪声比较有效,可保护仅有微小灰度差的图像细节。
3、几个常用模板
- 平均模板
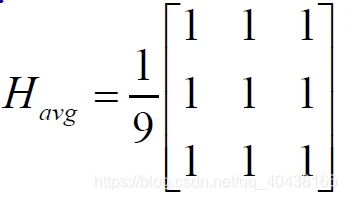
- 加权平均
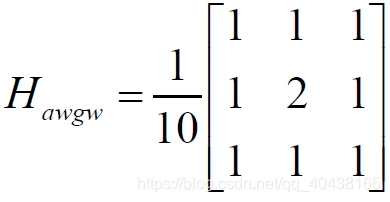
- 高斯模板
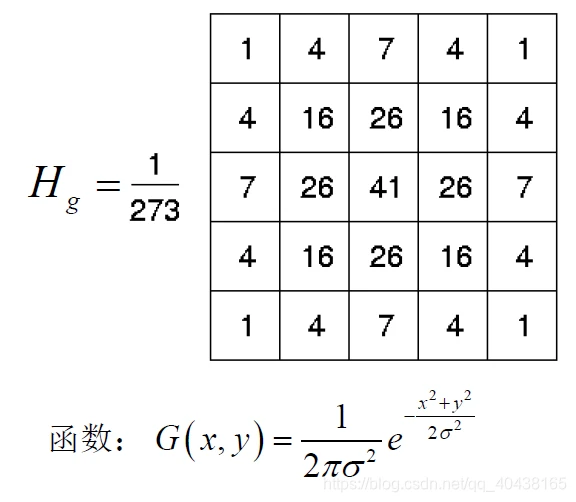
注:自动调节σ的值以实现权重调节。σ越小则中间值影响越大。
3、梯度倒数加权平均法
图像分布特点:
- 相邻区域之间的变化大于区域内部的变化;
- 同一区域中,中间像素的变化小于边缘像素的变化。
\quad
在不同区域交接的地方,梯度变化最快,梯度值很大,梯度倒数很小。这样我们给与一个较小的权重,以防太多的影响真实值。
梯度即为图像灰度变化率:
Δ
f
x
y
∼
f
(
x
+
1
,
y
+
1
)
−
f
(
x
,
y
)
\Delta f_{xy} \thicksim f(x+1,y+1)-f(x,y)
Δfxy∼f(x+1,y+1)−f(x,y)。
以梯度倒数
1
Δ
f
x
y
\frac{1}{\Delta f_{xy} }
Δfxy1做权重因子,则区域内部的邻点权重就大于边缘近旁或区域外的邻点。
2、中值滤波
用局部邻域像素灰度值排序后的中值代替当前像素的灰度值。
- 对点状噪声和干扰脉冲有良好的抑制作用。
- 能保持图像边缘,使原始图像不产生模糊。
- 缺点:对高斯噪声无能为力;计算比较费时。
3、锐化滤波器
\quad 图像锐化目的:加强图像轮廓,使图像看起来比较清晰、以便于对目标的识别和处理。图像锐化和平滑恰恰相反,它是通过增强高频分量来减少图像中的模糊,因此也称为高通滤波。
1、微分、梯度法
\quad
对于正弦函数
sin
(
2
π
a
x
)
\sin(2\pi ax)
sin(2πax),其微分为
2
π
a
cos
(
2
π
a
x
)
2\pi a \cos(2\pi ax)
2πacos(2πax)。可见微分后频率不变,幅度上升
2
π
a
2\pi a
2πa倍,且频率越高,上升幅度越大。这表明微分是可以加强高频成分的,从而使图像轮廓变清晰。
令
G
[
f
]
G[f]
G[f]为梯度算子,则
- g ( x , y ) = G ( f [ x , y ] ) g(x,y)=G(f[x,y]) g(x,y)=G(f[x,y]):轮廓比较突出,灰度平缓变化部分,梯度小,很黑。
- 突出轮廓,保留背景

- 背景保留,轮廓取单一灰度值

- 轮廓保留,背景取单一灰度值。

- 轮廓、背景分别取单一灰度值,即二值化。只对轮廓感兴趣。
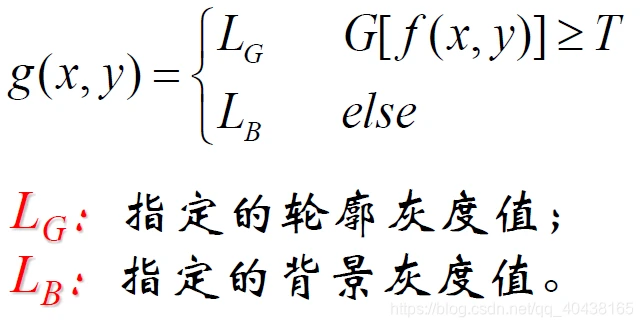
2、高通滤波法
\quad
边缘是由灰度级跳变点构成的,一般具有较高的空间频率。因此,采用高通滤波的方法让高频分量顺利通过,使低频分量得到抑制,就可增强高频分量,使图像的边缘或线条变的清晰,实现图像的锐化。
\quad
在空间域中,让图像和高通滤波器的冲击响应函数进行卷积。
\quad
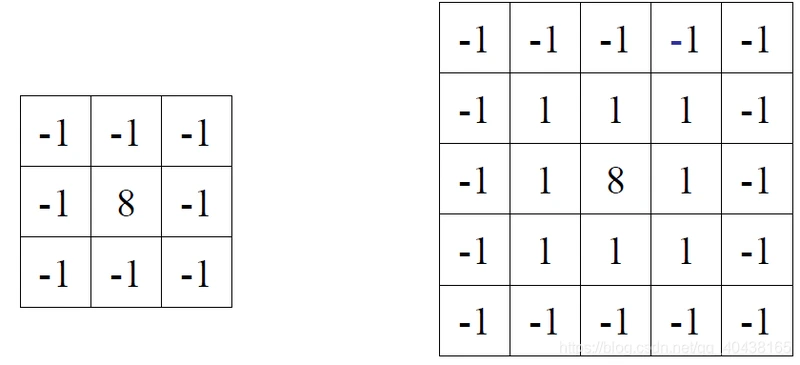
高通滤波器的设计
- kernel的中心系数与外围系数符号相反
- kernel系数和为0
3、反锐化掩模(核)
\quad 利用原图像减去平滑后的图像得到的结果构成反锐化模板
4、高提升滤波
\quad 将锐化的结果叠加于原图像
