公式结论：
对任意正数开根估算方法：要估算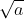
,只需取一个数m,那么估算结果约等于
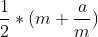,m和
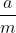越接近，这个估算越精确。
可以取28，675...验证。
理由：
微积分书上：
此处得到对1+无穷小量的开方估算方法：
学过微分线性近似后，得到一个结论：（1+无穷小）再开方与1+1/2*无穷小是等价无穷小，所以可以把开方运算转化为四则运算。
进一步对任意正数开方：
进一步推导求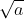可以转化为结论式子，具体怎么运用请看下面例子：
假设a=675,我们可以找到25*25(此处是要寻找比较靠近a的平方数m*m),
然后变形：根号下625+50，把625提出去，得到25*根号下1+0.08，转化为四则运算为25*（1+1/2*0.08）=26。
接下来验证a开平方能不能用26近似：26*26=676接近675，表明结果精度较高。
我们只需要用字母代替具体数字即可，如下：
对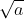，找到m,变形为
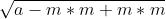，提出m*m为
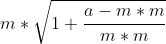,根号内第二项越接近0，这个式子越逼近于
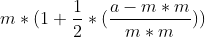，化简为。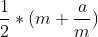
到这里已经是一个新的结论，因为我可以对它作出新的解释：
开根就是要找两个相等乘数m,m,使a=m*m，那么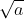=m;而对a=r*s,要找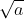，只需找一个r，让r,s靠近；r,s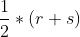越接近，
就越接近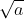。由此可以递推三次根：若a=b*c*d,那么找到b,c,使b,c,d越靠近，那么
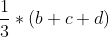就越接近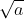（此处还没证明，慎用！！！）。