一元三次方程重根判别式_萌新也看得懂的三次方程解法和思路-CSDN博客

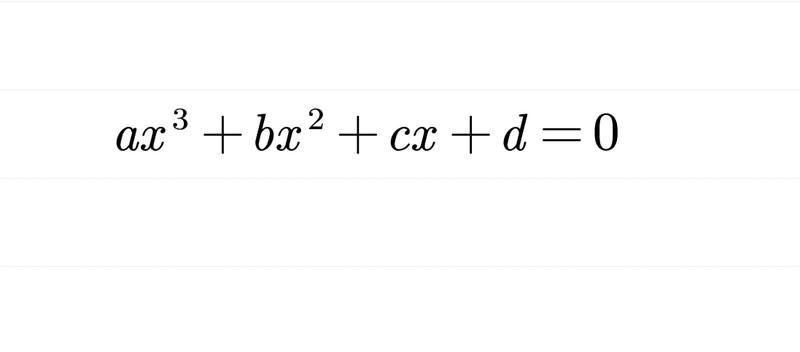
又来水一波文了，最近改写的没写，想法不少一个写不了唉，先祝大家中秋国庆双倍快乐。----2020.09.30

三次方程嘛，高中题有极低概率出现，因式分解的时候也喜欢出（因为三次方程的因式分解需要猜根或者得出一个解），学完一元二次方程的时候我也会对其感兴趣，那么我就用人话写一些关于一元三次方程的解法。

什么是一元三次方程?由一元二次方程的一般情况

当然，如果

不失一般性。当然这样对于初学者还是非常困难的，我们尝试从简单出发，由 特殊到一般。我们先列举三次方程的 最基本性质

1. 一元三次方程有三个根，既是它们可以包含复数根,而且至少有一个实数根。
2. 三次方程的韦达定理:

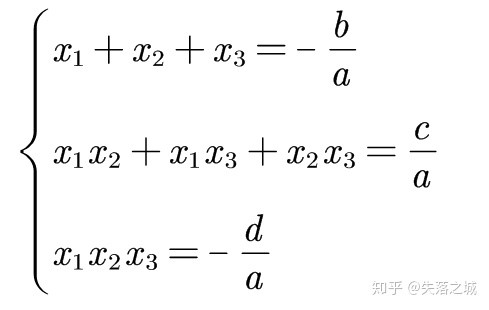
一.从最简单开始

如果三次方程有三个完全一样的根呢？那么类似一元二次方程我们可以知道它一定可以写成完全立方的形式，也就是

对比原方程的系数我们可以得到

消去

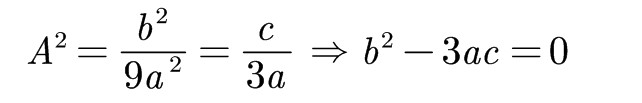
还有

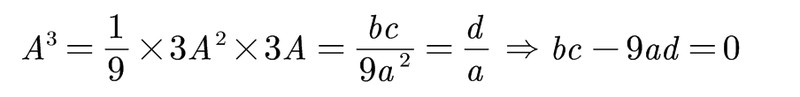
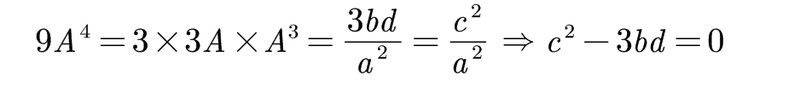
当然，还可以列举更多.这里，我们把

独立的了而是互相关联的，也就是说，如果同时满足（当然还可以有其他的等式，只需要三个就可以）

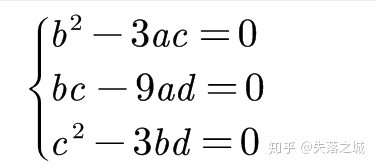
那么我们可以自豪地说:这个三次方程有三个完全相同的根！为了方便，我们可以把它们记作