第二十一章一元二次方程。

21.2 解一元二次方程。

21.2.4 一元二次方程的根与系数的关系。

1. 探索一元二次方程的根与系数的关系。（难点）

2. 不解方程利用一元二次方程的根与系数的关系解决问题。（重点）

1. 一元二次方程的求根公式是什么？

2. 如何用判别式 b2-4ac 来判断一元二次方程根的情况？

b2-4ac=0 时，方程有两个相等的实数根。b2-4ac<0 时，方程无实数根。

探索一元二次方程的根与系数的关系，算一算解下列方程并完成填空：

(1)x2+3x-4=0；

(2)x2-5x+6=0；

(3)2x2+3x+1=0。

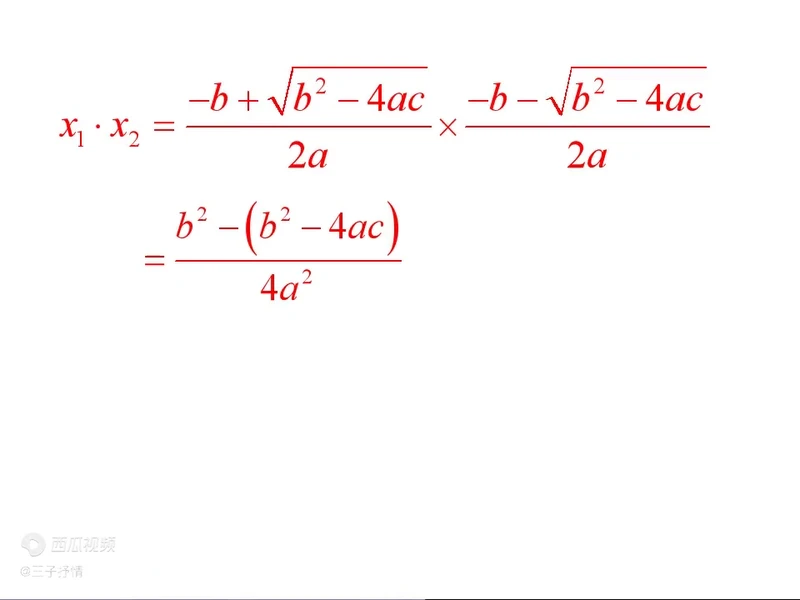
(1)若一元二次方程的两根为 xj、x，则有 x-x=0，且 x-x=0，那么方程(x-x)(x-x)=0（x、为已知数）的两根是什么？将方程化为 x2+px+q=0 的形式，你能看出 xj、x2 与 p、q 之间的关系。

(2)如果一元二次方程 ax2+bx+c=0（a≠0）的两个根分别是 x、x，那么，你可以发现什么结论？

一元二次方程的根与系数的关系（韦达定理）。如果一元二次方程 ax2+bx+c=0（a≠0）的两个根分别是 xj、x，那么满足上述关系的前提条件。

例 1 口答下列方程的两根之和与两根之积。下列方程的两根和与两根积各是多少？

见《学练优》课时练习。