20张图带你彻底搞懂二叉树的删除操作

vs心动
2,026 阅读10分钟

前言

最近在学习数据结构与算法，记录下二叉树的删除操作是如何实现的，相对于其他的插入，排序等操作。删除操作逻辑上稍微比较复杂，今天通过图形化的方式帮你们彻底搞懂到底是怎么实现删除操作的。话不多说，直接开始。
注：本文采用js语言作为演示

二叉树结构

我们如何用数据结构来表示出二叉树呢?
毫无疑问是对象的结构更符合我们的结果，我们直接定义一个类来帮我们生成节点。
这里我们就不探讨如何插入数据了，相对来说是比较简单。

// 二叉树的实现
// 创建节点
class CreateNode {
    right = null
    left = null
    constructor(key) {
        this.key = key
    }
}
class BinarySerachTree {
    // 根节点
    root = null
    // 查看遍历后的顺序
    traversal = []
    // 向树中插入数据 insert
    insert(key) {
        const newNode = new CreateNode(key)
        if (this.root === null) { // 没有根节点
            this.root = newNode
        } else {
            this.insertNode(this.root, newNode)
        }
    }
     // 判断插入的key大于还是小于节点
     // 再根据对应方向的子树是否为空 为空则直接赋值 否则继续递归查找
    insertNode(node, insertNode) {
        if (insertNode.key === node.key) return false
        if (insertNode.key < node.key) { //左子树
            if (node.left === null) { // 是否为空
                node.left = insertNode
                return true
            } else {
                this.insertNode(node.left, insertNode)
            }
        } else {//右子树
            if (node.right === null) { // 是否为空
                node.right = insertNode
                return true
            } else {
                this.insertNode(node.right, insertNode)
            }
        }

    }
    
  }

二叉树的删除操作

进入今天的正题，下面我们用这样的二叉树结构来模拟我们想要进行的删除操作。

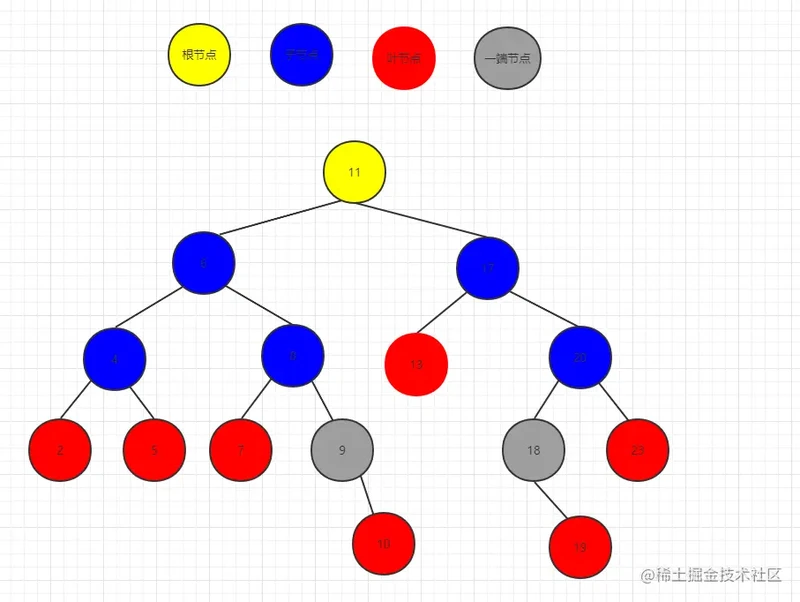
image.png

1.寻找要删除的节点

首先我们要做的是当条件给定我们一个节点让我们去执行删除操作，我们第一步应该是寻找到该条件对应的节点。
拿我们上面创建的结构来讲就是，通过 key 寻找到 newNode节点。
我们可以通过while循环依次比较大小寻找左右节点的方式来进行查找，例如我们要删除key为10的节点。
那么它的查找顺序应该是这样的

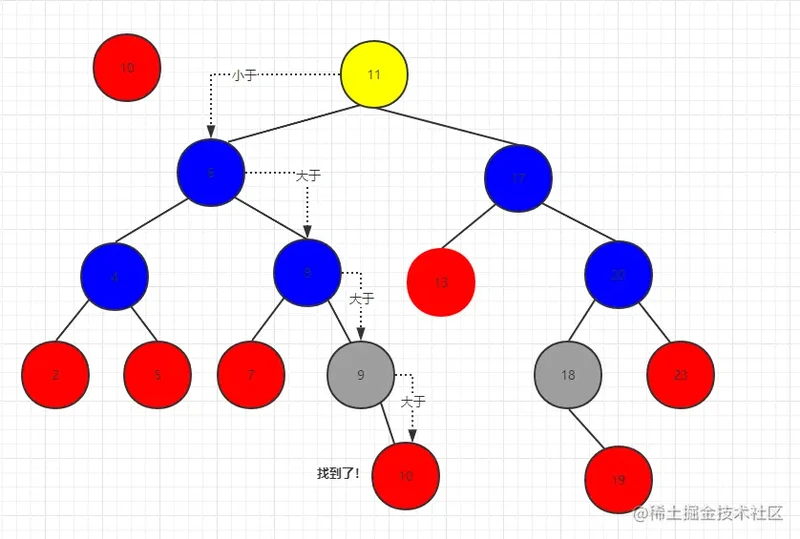
image.png

这时候我们来想想删除操作应该是怎样的呢？
就拿现在这个 10 节点来举例
9节点的右节点指向null --> 9.right = null
所以说我们要拿到删除节点的父节点
我们再来想一想 如果此时删除的是 7节点

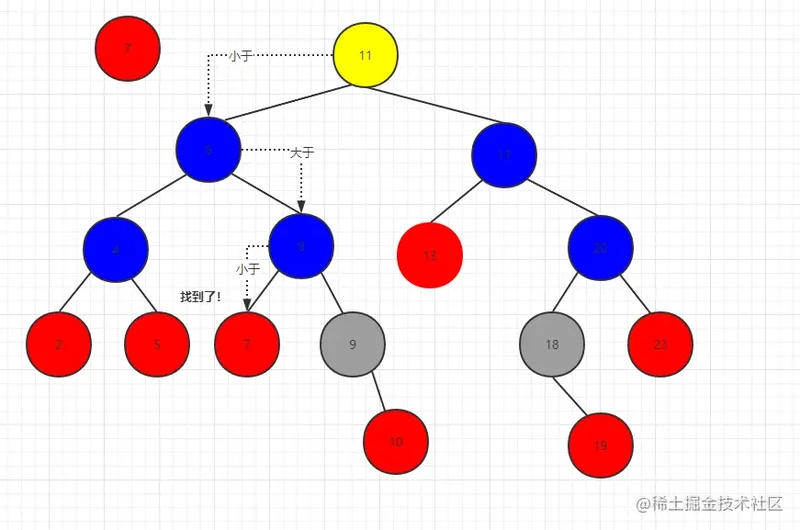image.png 那么操作应该是 --> 8.left = null
细心的同学就会发现，有时候是改左节点有时候是改右节点。
所以说我们还得记录下最后寻找节点的方向是左还是右，判断找到前是大于还是小于即可得到。
下面我们通过代码来实现:

class BinarySerachTree {
    // 根节点
    root = null
    // 查看遍历后的顺序
    traversal = []
     // 删除节点 remove
    remove(key) {
        // 1.寻找要删除的节点 父节点 节点方向
        let current = this.root //当前节点 根节点开始往下找
        let partent = null //当前节点的父节点
        let delNode = null // 找到要删除的节点   
        let isLeft = true // 记录最后是父节点的左还是右节点
        while (current) {// 直到找到最后为null
            if (key === current.key) {//找到了
                delNode = current
                current = false
            } else if (key > current.key) {//去当前节点的右节点找
                isLeft = false
                partent = current
                current = current.right
            } else {//去当前节点的左节点找
                isLeft = true
                partent = current
                current = current.left
            }
        }
        // 没有找到该节点
        if (!delNode) return false
        
  }

现在我们找到了删除节点以及其它的对应条件，下面我们要对此节点进行分析:

  1. 删除的节点是叶节点 即两端没有节点 左右节点为null
  2. 删除的节点只有一端节点 左节点为空或者右节点为空
  3. 删除的节点是完整的 即两端节点都有值

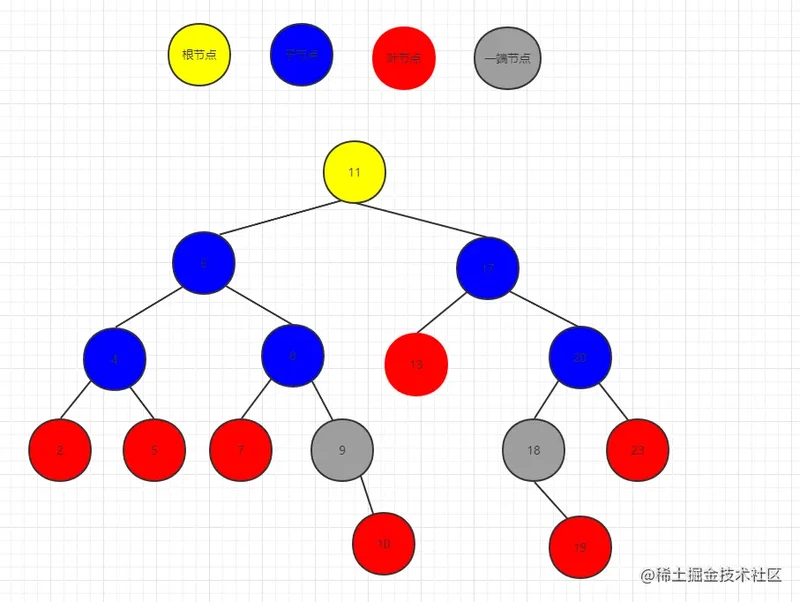
image.png

2.删除的节点是叶节点 即两端没有节点 左右节点为null

如果是这种情况我们还需要考虑

  1. 该节点是根节点
  2. 普通的叶节点

根节点删除图例:

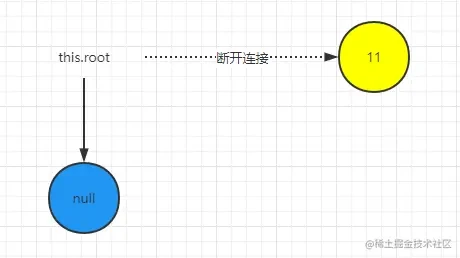image.png 只需要进行 this.root = null 初始化值就行了 11节点未被引用后面会被垃圾回收掉的

普通节点删除图例:
删除 7 节点 --> 8.left = null 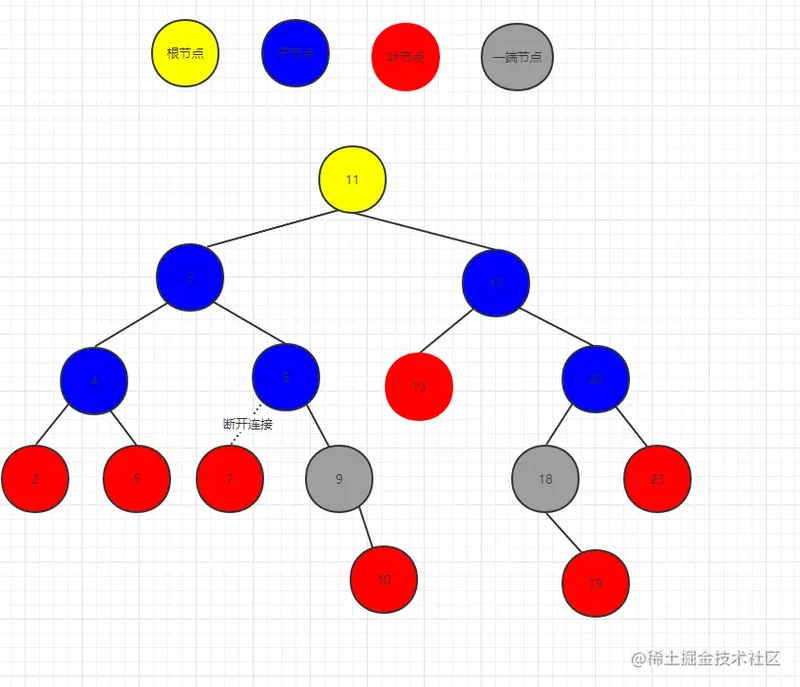image.png 删除 19节点 --> 18.right = null

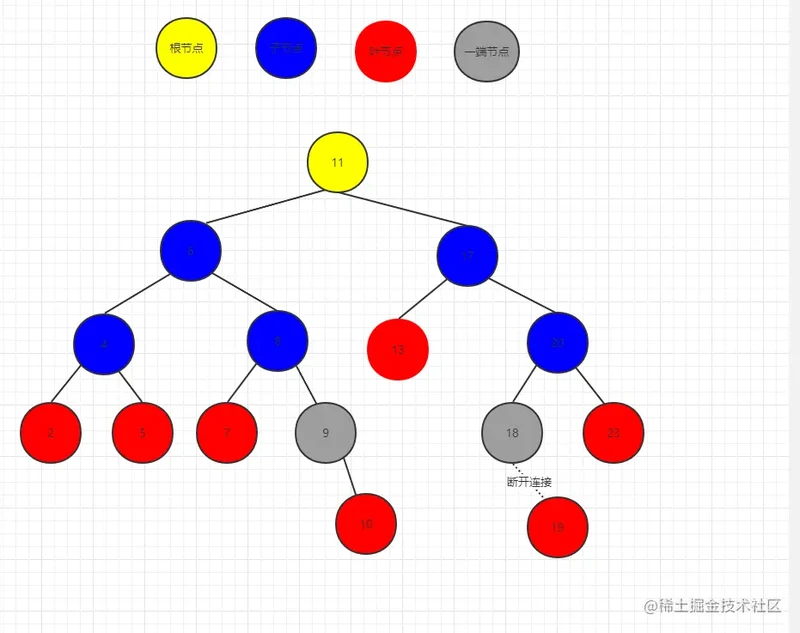image.png 我们只需要根据之前的isLeft参数就能知道删除节点是父节点的左还是右节点了！

class BinarySerachTree {
    // 根节点
    root = null
    // 查看遍历后的顺序
    traversal = []
     // 删除节点 remove
    remove(key) {
        // 1.寻找要删除的节点 父节点 节点方向
        let current = this.root //当前节点 根节点开始往下找
        let partent = null //当前节点的父节点
        let delNode = null // 找到要删除的节点   
        let isLeft = true // 记录最后是父节点的左还是右节点
        while (current) {// 直到找到最后为null
            if (key === current.key) {//找到了
                delNode = current
                current = false
            } else if (key > current.key) {//去当前节点的右节点找
                isLeft = false
                partent = current
                current = current.right
            } else {//去当前节点的左节点找
                isLeft = true
                partent = current
                current = current.left
            }
        }
        // 没有找到该节点
        if (!delNode) return false
         //2.如果删除的是叶节点 两端没有节点
        if (delNode.left === null && delNode.right === null) {
            if (delNode === this.root) {// 如果是根节点
                this.root = null
            } else {
                if (isLeft) {// 左节点
                    partent.left = null
                } else {
                    partent.right = null
                }
            }
        } 
  }

3.删除的节点是一端节点 即左节点为空或者右节点为空

这里也有四种情况

  1. 删除节点的是父节点左节点 且删除节点的右节点有值
  2. 删除节点的是父节点左节点 且删除节点的左节点有值
  3. 删除节点的是父节点右节点 且删除节点的右节点有值
  4. 删除节点的是父节点右节点 且删除节点的左节点有值

让我们通过图来看看吧
第一种情况：删除18节点

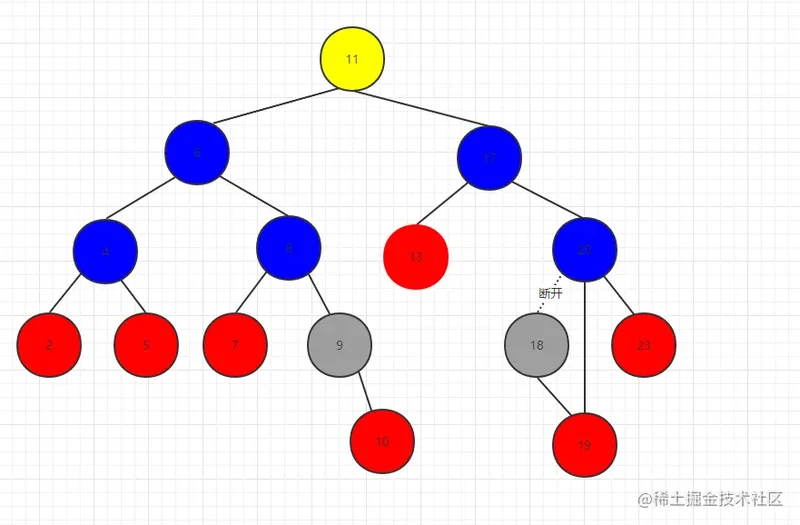
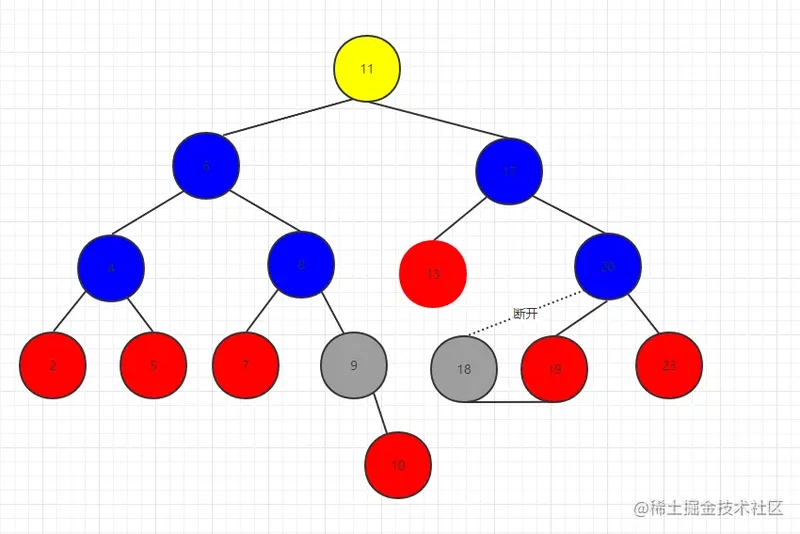image.png

image.png 我们只需要执行操作 20.left = 18.right
那么18.right 要不要重置为null呢？其实是不需要的，因为18引用了19但是它最后会被回收，因为从根节点找下来没有节点依赖于18，所以它会被回收掉。下面的也是同理哦！
第二种情况:删除19节点

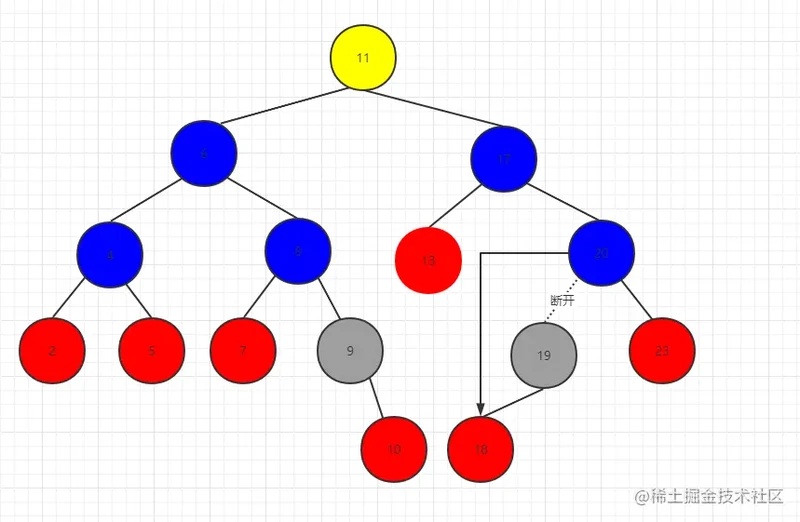
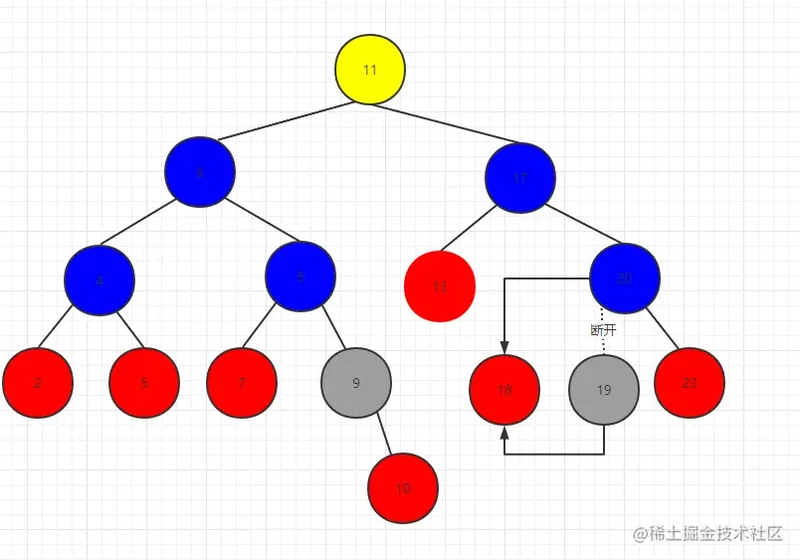image.png

image.png 同理可得 20.left = 19.left
第三种情况:删除9节点

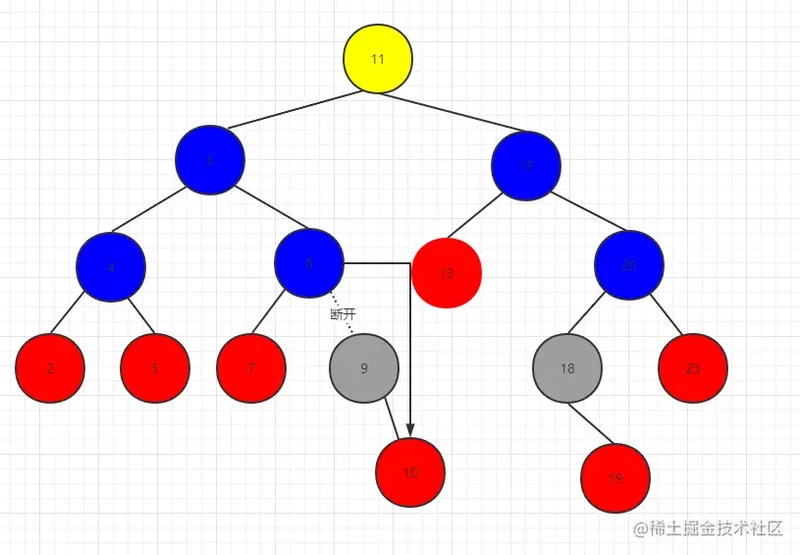image.png 同理可得 8.right = 9.right

第四种情况:删除10节点 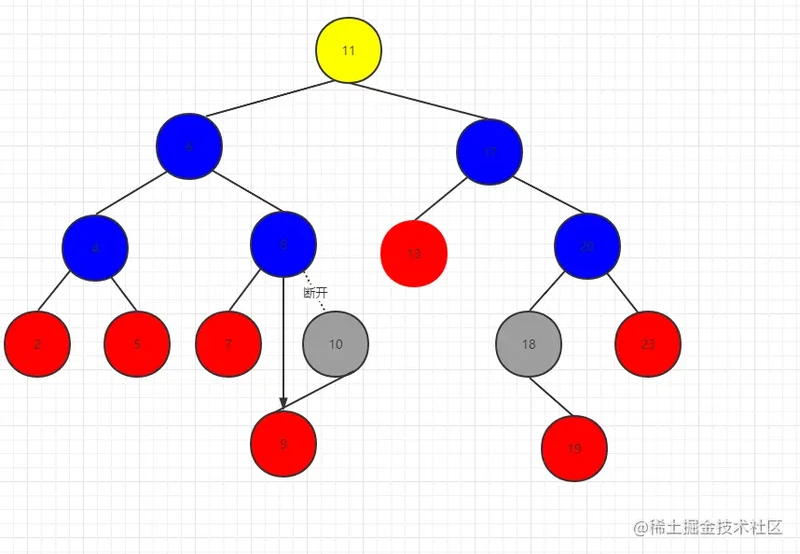image.png 同理可得 8.right = 10.left

代码实现:

class BinarySerachTree {
    // 根节点
    root = null
    // 查看遍历后的顺序
    traversal = []
   // 删除节点 remove
    remove(key) {
        // 1.寻找要删除的节点
        let current = this.root //当前节点
        let partent = null //当前节点的父节点
        let delNode = null // 找到要删除的节点   
        let isLeft = true // 记录最后是父节点的左还是右节点
        while (current) {
            if (key === current.key) {
                delNode = current
                current = false
            } else if (key > current.key) {
                isLeft = false
                partent = current
                current = current.right
            } else {
                isLeft = true
                partent = current
                current = current.left
            }
        }
        // 没有找到该节点
        if (!delNode) return false
        // 2.如果删除的是叶节点 两端没有节点
        if (delNode.left === null && delNode.right === null) {
            if (delNode === this.root) {// 如果是根节点
                this.root = null
            } else {
                if (isLeft) {// 左节点
                    partent.left = null
                } else {
                    partent.right = null
                }
            }
        //3.如果删除的节点有一端节点
        } else if (delNode.left === null) {// 左节点为空 右节点有值 右端有节点
            if (delNode === this.root) {// 如果是根节点
                this.root = delNode.right
            } else {
                if (isLeft) {// 左节点
                    partent.left = delNode.right
                } else {
                    partent.right = delNode.right
                }
            }
        } else if (delNode.right === null) {// 右节点为空 左节点有值 左端有节点
            if (delNode === this.root) {// 如果是根节点
                this.root = delNode.left
            } else {
                if (isLeft) {// 左节点
                    partent.left = delNode.left
                } else {
                    partent.right = delNode.left
                }
            }
        }
  }

4.删除的节点是完整的 即两端节点都有值

在写代码之前，我们先来了解一个概念，前驱 与 后继
只有找到了前驱或者后继节点我们才能真正的来删除完整节点
例如我们要删除根节点 11 那我们应该怎么做才能保持二叉树的结构呢？

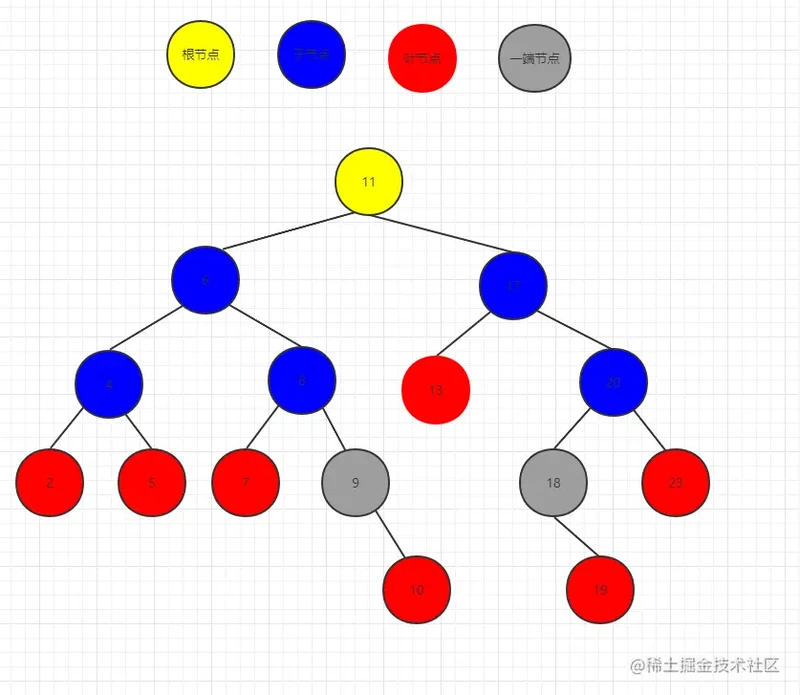image.png 聪明的你肯定能想到用 10 节点 或者 13节点来替代11节点，这样能保持我们的二叉树结构依然符合条件。
那么它到底有什么规律呢？
我们发现 10 节点是 11节点的左节点下的最右边的节点 前驱节点
而13 节点是 11节点的右节点的最左边的节点 后继节点
我们可以通过以下代码来实现:

// 找前驱的方法 getSuccessPre
    getSuccessPre(node) {// 传入被删节点
        let preNode = node.left
        let parent = node
        while (preNode.right) {
            parent = preNode
            preNode = preNode.right
        }
        return [preNode, parent]
    }
  // 找后继的方法 getSuccessor
    getSuccessor(node) {// 传入被删节点
        let sorNode = node.right
        let parent = node
        while (sorNode.left) {
            parent = sorNode
            sorNode = sorNode.left
        }
        return [sorNode, parent]
    }

那这里为什么也要保存对应的父节点呢？
如果我们删除的是6节点，这里采用寻找后继节点的方式来删除会进行一下操作:

  1. 6的后继节点找到了是 7节点

  2. 6的父节点（11）的左节点赋值给7节点 parent.left = 7

  3. 7的左右节点衔接6的左右节点 7.left = 6.left 7.right= 6.right

  4. 7节点的父节点的left重置为Null 不然会循环引用 8.left = null

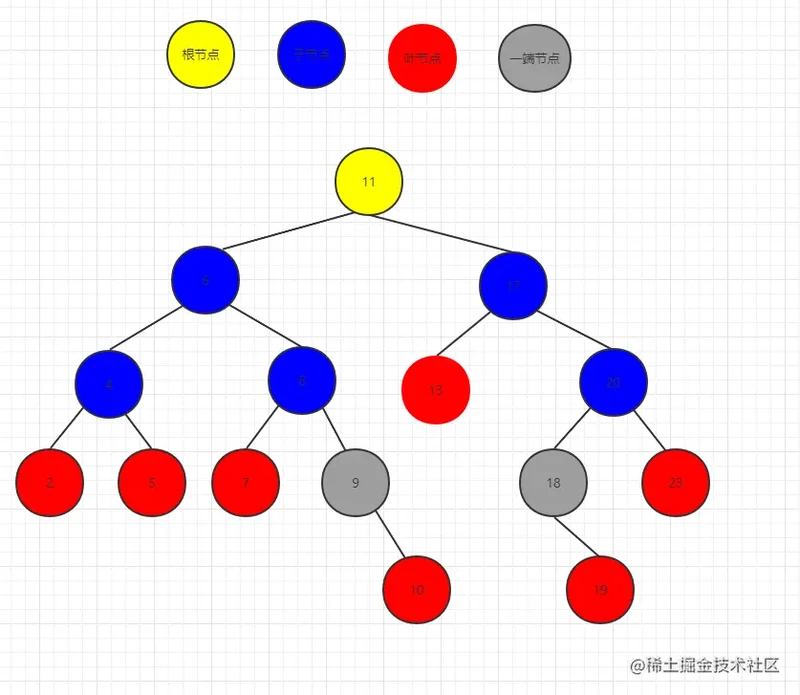
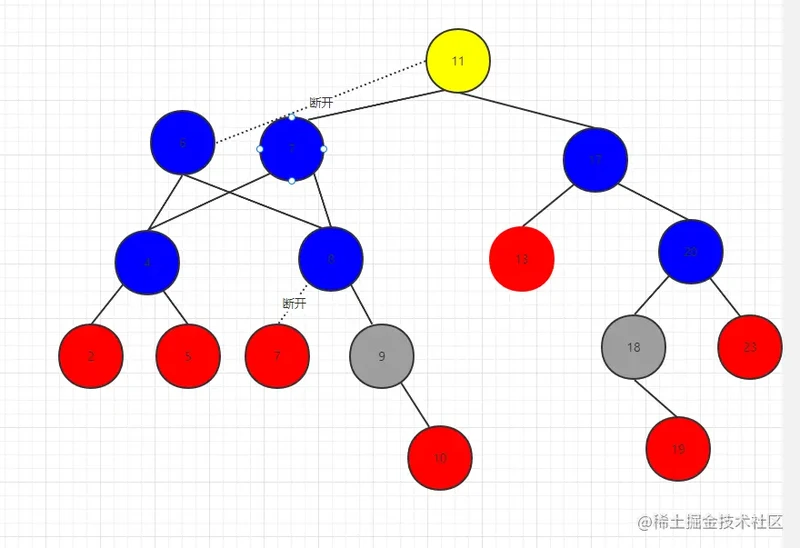image.png image.png 大功告成！
所以我们需要得到后继节点的父节点来断开之前的连接或者还有一种情况

如果我们删除的是17节点，这里采用寻找后继节点的方式来删除会进行一下操作:

  1. 17的后继节点找到了是 18节点
  2. 17的父节点（11）的左节点赋值给18节点 parent.left = 18
  3. 18节点的父节点的left指向19节点 20.left = 18.right
  4. 18的左右节点衔接17的左右节点 18.left = 17.left 18.right= 17.right
    注意 三四步骤的顺序不能颠倒！ 我们可以看到这样也需要运用后继节点的父节点来接纳后继节点的右节点。
    那会不会有这样的一种情况，需要接纳的是后继节点的左节点呢？
    答案是不会的！如果你了解了后继的真正概念你就会发现，后继节点的左节点一定是空的，否则后继节点就不是当前的节点，而应该是该节点的左子节点了！

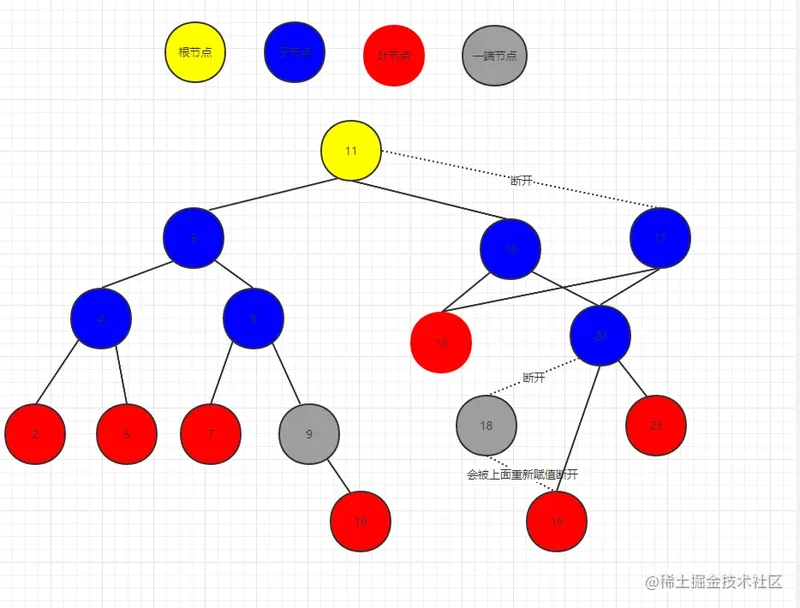image.png image.png 上面描述的两种情况其实可以统一进行处理，我们只需要执行:

  1. 被删的后继节点找到了是 后继节点
  2. parent的左节点赋值给后继节点 parent.left = 后继
  3. 后继节点的父节点的left指向后继右节点 后继parent.left = 后继.right
  4. 后继的左右节点衔接被删的左右节点 后继.left = 被删.left 后继.right= 被删.right

步骤三中将后继没有右节点的情况也包含了，没有的话后继的右节点就是null

下面我们来讨论另外一种情况:
这里以删除8节点为例:

  1. 寻找8节点的后继 为9节点
  2. 8的父节点指向 9节点 parent = 9
  3. 9的左节点指向8的左节点 9.left = 8.left
    我们发现后继节点就是被删节点的右节点

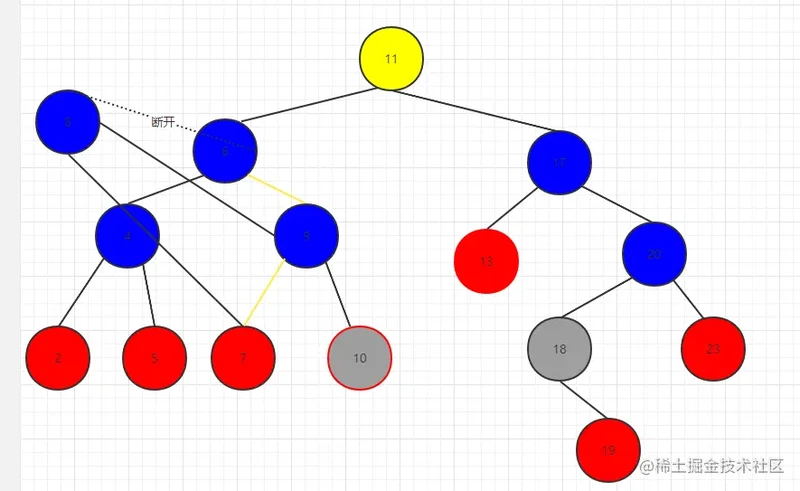
image.png

image.png

总结成功！开始分情况写代码:

class BinarySerachTree {
    // 根节点
    root = null
    // 查看遍历后的顺序
    traversal = []
  // 删除节点 remove
    remove(key) {
        // 1.寻找要删除的节点
        let current = this.root //当前节点
        let partent = null //当前节点的父节点
        let delNode = null // 找到要删除的节点   
        let isLeft = true // 记录最后是父节点的左还是右节点
        while (current) {
            if (key === current.key) {
                delNode = current
                current = false
            } else if (key > current.key) {
                isLeft = false
                partent = current
                current = current.right
            } else {
                isLeft = true
                partent = current
                current = current.left
            }
        }
        // 没有找到该节点
        if (!delNode) return false
        // 2.如果删除的是叶节点 两端没有节点
        if (delNode.left === null && delNode.right === null) {
            if (delNode === this.root) {// 如果是根节点
                this.root = null
            } else {
                if (isLeft) {// 左节点
                    partent.left = null
                } else {
                    partent.right = null
                }
            }
        //3.如果删除的节点有一端节点
        } else if (delNode.left === null) {// 左节点为空 右节点有值 右端有节点
            if (delNode === this.root) {// 如果是根节点
                this.root = delNode.right
            } else {
                if (isLeft) {// 左节点
                    partent.left = delNode.right
                } else {
                    partent.right = delNode.right
                }
            }
        } else if (delNode.right === null) {// 右节点为空 左节点有值 左端有节点
            if (delNode === this.root) {// 如果是根节点
                this.root = delNode.left
            } else {
                if (isLeft) {// 左节点
                    partent.left = delNode.left
                } else {
                    partent.right = delNode.left
                }
            }
        } else {// 4.两端都有节点
            let [successsor, sorParent] = this.getSuccessor(delNode)
            if (delNode === sorParent) { //后继节点的父节点是被删节点
                if (delNode === this.root) {// 如果是根节点
                    this.root = successsor
                } else {
                    partent.right = successsor
                }
                successsor.left = delNode.left
            } else {// 后继节点父节点不是被删节点
                if (delNode === this.root) {// 如果是根节点
                    this.root = successsor
                } else if (isLeft) { // 根据被删节点再父节点的位置选择合适的位置进行替换
                    partent.left = successsor
                } else {
                    partent.right = successsor
                }
                sorParent.left = successsor.right
                successsor.left = delNode.left
                successsor.right = delNode.right
            }
        }
        return true
    }
     
     // 找前驱的方法 getSuccessPre
    getSuccessPre(node) {
        let preNode = node.left
        let parent = node
        while (preNode.right) {
            parent = preNode
            preNode = preNode.right
        }
        return [preNode, parent]
    }
    // 找后继的方法 getSuccessor
    getSuccessor(node) {
        let sorNode = node.right
        let parent = node
        while (sorNode.left) {
            parent = sorNode
            sorNode = sorNode.left
        }
        return [sorNode, parent]
    }
     
     // 中序遍历 inOrderTraversal
    inOrderTraversal() {
        this.traversal = []
        this.inOrderTraversalNode(this.root)
    }
    inOrderTraversalNode(node) {
        if (node) {
            this.inOrderTraversalNode(node.left)
            this.traversal.push(node.key)
            this.inOrderTraversalNode(node.right)
        }
    }
  }

终于是写完了！我们可以通过代码里的中序遍历来验证，如果是从小到大排序说明成功实现了！
快来动手写一写吧！

End

如果此文对你有帮助欢迎大家点赞收藏加关注！如有不对之处，望各位大佬不吝赐教。
三连加关注，更新不迷路！

QQ图片20200210181218.jpg