任意方程求根
全文目录
(博客园)机器学习
(Github)MachineLearning Math
1.简介
方程和函数是代数数学中最为重要的内容之一,从初中直到大学,我们都在研究着方程与函数,甚至我们将图形代数化,从而发展出了代数几何、解析几何的内容。而在方程与函数中,我们研究其性质最多的,往往就是方程的根(零点),即使是研究方程的极值点、鞍点等,我们无非也只是研究其微商的零点。
我们在初等数学中已经学过许多简单初等函数、线性方程的求解方法,在本文中,我们重点讨论任意方程,尤其是计算困难的非线性方程的求根方法。
2.方程
2.1分类和介绍
方程就是指含有未知数的等式。是表示两个数学式(如两个数、函数、量、运算)之间相等关系的一种等式,使等式成立的未知数的值称为“解”或“根”。在这里,根据一些性质的不同,我们将方程分成以下几类:
单个方程
线性方程:本质是等式两边乘以任何相同的非零数,方程的本质都不受影响。通常认为只含有一次项的方程。
非线性方程:是因变量与自变量之间的关系不是线性的关系的方程。
多项式方程
超越方程:指含有未知量的超越式(指数、对数、三角函数、反三角函数等)的方程。换言之,超越方程中都有无法用含有未知数的多项式、分式或开方表示的式子。
多个方程
2.2方程的零点(根、解)
若有一个值或一些值能够使得方程 f ( x ) = 0 f(x)=0 f ( x ) = 0
若方程有且只有一个解x ∗ x^* x ∗ x ∗ x^* x ∗
若对于方程f ( x ) = 0 f(x)=0 f ( x ) = 0 f ( x ∗ ) = 0 , f ′ ( x ∗ ) = f ′ ′ ( x ∗ ) = ⋯ = f ( k ) ( x ∗ ) = 0 , f ( k + 1 ) ( x ∗ ) ≠ 0 f(x^*) = 0,f^{'}(x^*)=f^{''}(x^*)=\cdots=f^{(k)}(x^*)=0,f^{(k+1)}(x^*)\neq0 f ( x ∗ ) = 0 , f ′ ( x ∗ ) = f ′′ ( x ∗ ) = ⋯ = f ( k ) ( x ∗ ) = 0 , f ( k + 1 ) ( x ∗ ) = 0 x ∗ x^* x ∗
PS:若方程是简单幂函数多项式组成,那么方程的解的数量应和最高此项的数值一致,因为存在虚根。
3.求根方法
求根的方法基本上大同小异,都是通过区间去逼近方程的根的点。
首先我们说一个定理1:对于实函数方程f ( x ) = 0 f(x)=0 f ( x ) = 0 x ∈ ( a , b ) x\in(a,b) x ∈ ( a , b ) f ( x ) f(x) f ( x ) x ∈ ( a , b ) x\in(a,b) x ∈ ( a , b ) f ( a ) ⋅ f ( b ) < 0 f(a)\cdot f(b)<0 f ( a ) ⋅ f ( b ) < 0 x ∈ ( a , b ) x\in(a,b) x ∈ ( a , b )
3.1二分法
3.1.1普通二分法的原理及操作
二分法和算法中的二分搜索法非常的类似,取定有根区间[ a , b ] [a,b] [ a , b ] m i d = a + b 2 mid = \frac{a+b}{2} mi d = 2 a + b f ( a ) ⋅ f ( m i d ) < 0 f(a)\cdot f(mid)<0 f ( a ) ⋅ f ( mi d ) < 0 b = m i d b=mid b = mi d f ( b ) ⋅ f ( m i d ) < 0 f(b)\cdot f(mid)<0 f ( b ) ⋅ f ( mi d ) < 0 a = m i d a=mid a = mi d ∣ b n − a n ∣ < ϵ |b_n-a_n|<\epsilon ∣ b n − a n ∣ < ϵ
产生的截断误差为∣ e n − 1 ∣ = x n + 1 − x ∗ ≤ [ b n − a n ] = b 0 − a 0 2 n |e_{n-1}| = x_{n+1} - x^*\leq[b_n - a_n] = \frac{b_0 - a_0}{2^n} ∣ e n − 1 ∣ = x n + 1 − x ∗ ≤ [ b n − a n ] = 2 n b 0 − a 0
可以计算出最小迭代次数为n = l g ( c 0 − a 0 ) − l g ϵ l g 2 n = \frac{lg(c_0-a_0)-lg\epsilon}{lg2} n = l g 2 l g ( c 0 − a 0 ) − l g ϵ
代码实现(更多语言的代码见仓库中Code文件夹):
private static double epsilon = 0.001 ;
public static double Binary (Func<double , double > func, double a, double b )var f1 = func.Invoke(a);
var f2 = func.Invoke(b);
if (f1 * f2 > 0 )
throw new ArgumentException("此区间无根或根不唯一" );
double mid = (a + b) / (double )2 ;
var fm = func.Invoke(mid);
if (fm == 0 )
return fm;
if (f1 * fm < 0 )
b = mid;
else if (f2 * fm < 0 )
a = mid;
if (Math.Abs(b - a) <= epsilon)
return (a + b) / (double )2 ;
return Binary(func, a, b);
}
3.1.2普通二分法准确度及速度分析
假设[ a , b ] \left[a,b\right] [ a , b ] [ a n , b n ] [a_n,b_n] [ a n , b n ] ( b − a ) / 2 n (b-a)/2^n ( b − a ) / 2 n
e = ∣ x c − r ∣ < b − a 2 n + 1 e = \left|x_c-r\right|<\frac{b-a}{2^{n+1}} e = ∣ x c − r ∣ < 2 n + 1 b − a 若e < 1 2 × 1 0 − p e<\frac{1}{2}\times10^{-p} e < 2 1 × 1 0 − p
事实上我们也可以简单的计算出函数执行的次数为n+2次。
3.2浅谈迭代
3.2.1 迭代是什么
迭代是重复反馈过程的活动,其目的通常是为了逼近所需目标或结果。每一次对过程的重复称为一次“迭代”,而每一次迭代得到的结果会作为下一次迭代的初始值。
重复执行一系列运算步骤,从前面的量依次求出后面的量的过程。此过程的每一次结果,都是由对前一次所得结果施行相同的运算步骤得到的。这篇文章中对于迭代有一个非常不错的概述究竟什么是迭代?
3.2.2 不动点的定义
各位可以尝试以下操作,
随意输入一个数字λ \lambda λ
然后对其进行c o s λ cos\lambda cos λ
将运算结果作为新的值传回c o s x cosx cos x
当你一直重复以上三个操作,你会发现数字最后会定格在0.73908513左右不动了。这是一个非常有趣的现象,事实上我们的这个操作就是x n = c o s x n − 1 x_n = cosx_{n-1} x n = cos x n − 1 x = c o s x x = cosx x = cos x
这就是我们不动点的一种实际情况,不动点原理是数学上一个重要的原理,也叫压缩映像原理或巴拿赫(Banach)不动点定理,完整的表达:完备的度量空间上,到自身的一个压缩映射存在唯一的不动点。用初等数学可以这么理解:连续映射f f f x x x f ( x ) = x f(x)=x f ( x ) = x
若某函数满足f ( λ ) = λ , λ ∈ R f(\lambda)=\lambda,\lambda \in R f ( λ ) = λ , λ ∈ R λ \lambda λ f ( f ( λ ) ) = λ , λ ∈ R f(f(\lambda))=\lambda,\lambda \in R f ( f ( λ )) = λ , λ ∈ R
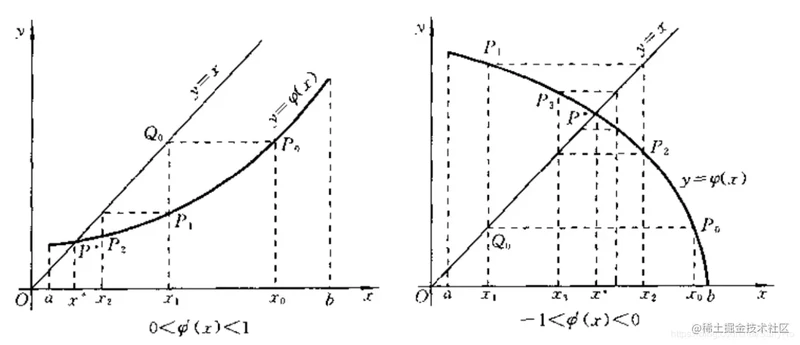
不动点的存在定理 :若某函数y = f ( x ) y=f(x) y = f ( x ) y = x y=x y = x
3.2.3 函数的相似性
我们常常说图形之间的相似,事实上函数也有其相似的定义。若函数f ( x ) f(x) f ( x ) t = φ ( x ) , x = φ − 1 ( t ) , f ( x ) = > f ( φ − 1 ( t ) ) t = \varphi(x),x=\varphi^{-1}(t),f(x)=>f(\varphi^{-1}(t)) t = φ ( x ) , x = φ − 1 ( t ) , f ( x ) => f ( φ − 1 ( t )) f ( x 0 ) = x 1 = t , f ( x 1 ) = f ( f ( x 0 ) ) = f ( t ) = x 2 . . . f(x_0) = x_1 = t,f(x_1)=f(f(x_0))=f(t)=x_2... f ( x 0 ) = x 1 = t , f ( x 1 ) = f ( f ( x 0 )) = f ( t ) = x 2 ... f ( f ( x ) ) f(f(x)) f ( f ( x )) f ( φ − 1 ( t ) ) f(\varphi^{-1}(t)) f ( φ − 1 ( t ))
现在做出如下变换,将外层的f ( x ) f(x) f ( x ) f ( φ − 1 ( t ) ) f(\varphi^{-1}(t)) f ( φ − 1 ( t )) g ( t ) = φ ( f ( φ − 1 ( t ) ) ) g(t) = \varphi(f(\varphi^{-1}(t))) g ( t ) = φ ( f ( φ − 1 ( t ))) g ( x ) g(x) g ( x ) g ( g ( t ) ) = φ ( f ( f ( φ − 1 ( t ) ) ) g(g(t)) = \varphi(f(f(\varphi^{-1}(t))) g ( g ( t )) = φ ( f ( f ( φ − 1 ( t ))) g n ( t ) = φ ( f n ( φ − 1 ( t ) ) ) g_n(t) = \varphi(f_n(\varphi^{-1}(t))) g n ( t ) = φ ( f n ( φ − 1 ( t )))
我们在这给出总结和定义:若函数g ( x ) , f ( x ) , φ ( x ) g(x),f(x),\varphi(x) g ( x ) , f ( x ) , φ ( x ) g ( x ) = φ ( f ( φ − 1 ( x ) ) ) g(x)=\varphi(f(\varphi^{-1}(x))) g ( x ) = φ ( f ( φ − 1 ( x ))) g ( x ) g(x) g ( x ) f ( x ) f(x) f ( x ) φ ( x ) \varphi(x) φ ( x ) f ∼ g f\sim g f ∼ g φ ( x ) \varphi(x) φ ( x ) g ∼ f = > g n ∼ f n g\sim f=>g^n\sim f^n g ∼ f => g n ∼ f n
若函数 g ( x ) 的不动点为 x 0 ,则有 若函数g(x)的不动点为x_0,则有 若函数 g ( x ) 的不动点为 x 0 ,则有 g ( x 0 ) = x 0 = φ ( f ( φ − 1 ( x 0 ) ) ) g(x_0)=x_0=\varphi(f(\varphi^{-1}(x_0))) g ( x 0 ) = x 0 = φ ( f ( φ − 1 ( x 0 ))) 根据反函数性质有 φ ( φ − 1 ( x ) ) = x 根据反函数性质有\varphi(\varphi^{-1}(x))=x 根据反函数性质有 φ ( φ − 1 ( x )) = x 故 f ( φ − 1 ( x 0 ) ) = φ − 1 ( x 0 ) = x 0 , φ − 1 ( x 0 ) 是 f ( x ) 的一个不动点 故f(\varphi^{-1}(x_0)) = \varphi^{-1}(x_0)=x_0,\varphi^{-1}(x_0)是f(x)的一个不动点 故 f ( φ − 1 ( x 0 )) = φ − 1 ( x 0 ) = x 0 , φ − 1 ( x 0 ) 是 f ( x ) 的一个不动点 通过上述得出的不动点,很容易通过刚才讲的内容得出φ − 1 ( x 0 ) \varphi^{-1}(x_0) φ − 1 ( x 0 ) g ( x ) g(x) g ( x )
3.2.4 迭代收敛速度
迭代是一种逼近、利用数列、函数收敛的性质进行求解的方法,那么对于收敛的速度,我们很难直接从数值看出速度,因为收敛过程中,误差的变化是越来越小的,因此我们再次进行一个比阶。
∃ p ∈ N & C > 0 , lim k → ∞ e k + 1 e k p = C \exists p\in N \And C>0,\displaystyle \lim_{k \to \infty}\frac{e_{k+1}}{e_k^p} = C ∃ p ∈ N & C > 0 , k → ∞ lim e k p e k + 1 = C
其中:
e k = ∣ x k − x ∗ ∣ e_k = |x_k-x^*| e k = ∣ x k − x ∗ ∣
p = { p = 1 , 线性收敛 p = 2 , 平方收敛 p > 2 , 高阶收敛 p=
\begin{cases}
p=1,线性收敛\\
p=2,平方收敛\\
p>2,高阶收敛
\end{cases} p = ⎩ ⎨ ⎧ p = 1 , 线性收敛 p = 2 , 平方收敛 p > 2 , 高阶收敛 并且有一个定理:若φ ( x ) \varphi(x) φ ( x ) x ∗ x^* x ∗ ∣ φ ′ ( x ) ∣ < 1 |\varphi^{'}(x)|<1 ∣ φ ′ ( x ) ∣ < 1
当φ ′ ( x ) ≠ 0 \varphi^{'}(x)\neq0 φ ′ ( x ) = 0
当φ ′ ( x ) = 0 , φ ′ ′ ( x ) ≠ 0 \varphi^{'}(x)=0,\varphi^{''}(x)\neq0 φ ′ ( x ) = 0 , φ ′′ ( x ) = 0
证明过程留给读者,只需要利用泰勒展开是便可以证明该定理。
3.3不动点迭代法
3.3.1不动点迭代法的原理及操作
迭代法是将方程求根问题转换成了函数求交点问题再转换成数列求极限的问题,这个过程中,对方程进行一个巧妙的变换之后,方程就可以在若干次迭代之后解出一个近似解。
操作方法如下:首先将方程f ( x ) = 0 f(x)=0 f ( x ) = 0 x = g ( x ) x = g(x) x = g ( x ) y = x y=x y = x y = g ( x ) y=g(x) y = g ( x ) x 0 x_0 x 0 x 1 = g ( x 0 ) x_1 = g(x_0) x 1 = g ( x 0 ) lim k → ∞ x k \displaystyle \lim_{k \to \infty}x_k k → ∞ lim x k x k x_k x k
我们即使构造出了x = g ( x ) x=g(x) x = g ( x ) φ ( x ) ∼ g ( x ) \varphi(x)\sim g(x) φ ( x ) ∼ g ( x ) ∣ φ ′ ( x ) ∣ < 1 |\varphi^{'}(x)|<1 ∣ φ ′ ( x ) ∣ < 1
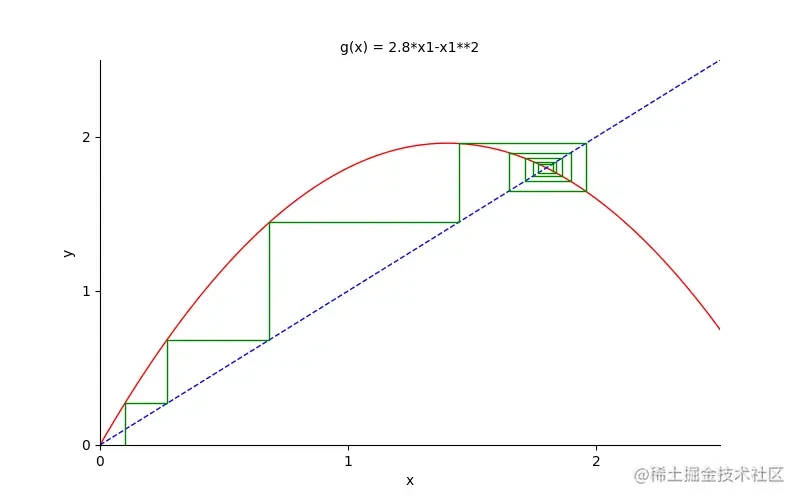
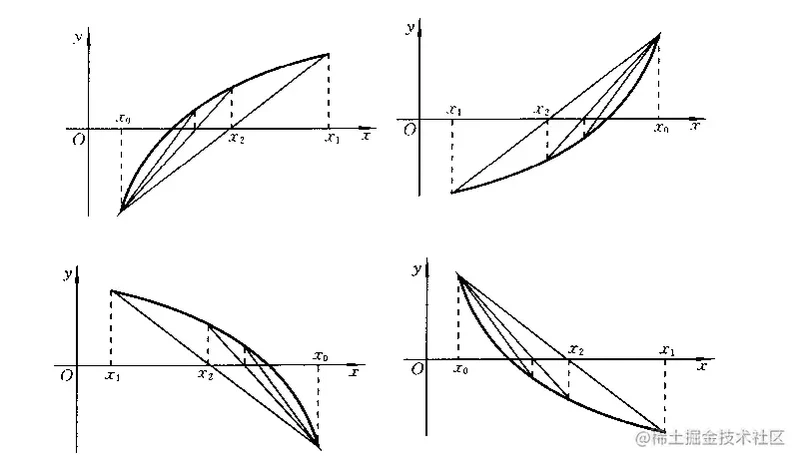
迭代过程收敛的情况如下图所示:
如果说我们的导数不满足条件,那么我们的迭代将会发散:
代码样例
public static double Iterative (Func<double , double > func, double x )double temp = func.Invoke(x);
if (Math.Abs(temp - x) <= epsilon)
{
return temp;
}
x = temp;
return Iterative(func, x);
}
3.3.2迭代法的收敛性证明
在这里,我们将证明迭代法求根的合理性和可行性。
前提条件:设函数φ ( x ) , x ∈ [ a , b ] \varphi(x), x\in[a,b] φ ( x ) , x ∈ [ a , b ]
∀ x ∈ [ a , b ] , φ ( x ) ∈ [ a , b ] \forall x\in [a,b],\varphi(x)\in[a,b] ∀ x ∈ [ a , b ] , φ ( x ) ∈ [ a , b ]
∃ L ∈ ( 0 , 1 ) , ∀ x ∈ [ a , b ] , ∣ φ ′ ( x ) ∣ ≤ L \exists L \in (0,1),\forall x\in[a,b],|\varphi^{'}(x)|\leq L ∃ L ∈ ( 0 , 1 ) , ∀ x ∈ [ a , b ] , ∣ φ ′ ( x ) ∣ ≤ L
要证明和解决以下命题和问题:
在x ∈ [ a , b ] , ∃ x ∗ , φ ( x ∗ ) = 0 x\in[a,b],\exists x^*,\varphi(x^*) = 0 x ∈ [ a , b ] , ∃ x ∗ , φ ( x ∗ ) = 0
∀ x 0 ∈ [ a , b ] \forall x_0\in[a,b] ∀ x 0 ∈ [ a , b ] x k + 1 = φ ( x k ) x_{k+1} = \varphi(x_k) x k + 1 = φ ( x k ) x ∗ x^* x ∗
求解误差分析式
现在开始证明
1:证明在区间内有且只有一个根存在:
证:在x ∈ [ a , b ] x \in [a,b] x ∈ [ a , b ] φ ′ ( x ) \varphi^{'}(x) φ ′ ( x ) φ ( x ) \varphi(x) φ ( x ) g ( x ) = x − φ ( x ) g(x) = x - \varphi(x) g ( x ) = x − φ ( x ) g ( x ) g(x) g ( x )
又因为φ ( x ) ∈ [ a , b ] \varphi(x) \in [a,b] φ ( x ) ∈ [ a , b ] g ( a ) ∗ g ( b ) < 0 g(a)*g(b)<0 g ( a ) ∗ g ( b ) < 0 x = φ ( x ) x=\varphi(x) x = φ ( x )
利用反证法:若在[a,b]上还有一实根x ˉ \bar{x} x ˉ
x ∗ − x ˉ = φ ( x ∗ ) − φ ( x ˉ ) = φ ′ ( ξ ) ( x ∗ − x ˉ ) ⟹ φ ′ ( ξ ) = 1 x^*-\bar{x} = \varphi(x^*)-\varphi(\bar{x}) = \varphi^{'}(\xi)(x^*-\bar{x})\Longrightarrow \varphi^{'}(\xi) = 1 x ∗ − x ˉ = φ ( x ∗ ) − φ ( x ˉ ) = φ ′ ( ξ ) ( x ∗ − x ˉ ) ⟹ φ ′ ( ξ ) = 1
显然与假设不符合。
2:证明这个根收敛于x ∗ x^* x ∗
根据拉格朗日中值定理,容易知道
x ∗ − x k + 1 = φ ( x ∗ ) − φ ( x k ) = φ ′ ( ξ ) ( x ∗ − x k ) x^*-x_{k+1} = \varphi(x^*)-\varphi(x_k) = \varphi^{'}(\xi)(x^*-x_k) x ∗ − x k + 1 = φ ( x ∗ ) − φ ( x k ) = φ ′ ( ξ ) ( x ∗ − x k )
又因∣ φ ′ ( x ) ∣ ≤ L |\varphi^{'}(x)|\leq L ∣ φ ′ ( x ) ∣ ≤ L
∣ x ∗ − x k + 1 ∣ ≤ ∣ L ( x ∗ − x k ) ∣ = ∣ L 2 ( x ∗ − x k − 1 ) = ⋯ = ∣ L k ( x ∗ − x 0 ) ∣ |x^*-x_{k+1}|\leq|L(x^*-x_k)|=|L^2(x^*-x_{k-1})=\cdots=|L^k(x^*-x_0)| ∣ x ∗ − x k + 1 ∣ ≤ ∣ L ( x ∗ − x k ) ∣ = ∣ L 2 ( x ∗ − x k − 1 ) = ⋯ = ∣ L k ( x ∗ − x 0 ) ∣
因为lim k → ∞ L k = 0 \displaystyle \lim_{k \to \infty}L^k=0 k → ∞ lim L k = 0 lim k → ∞ ∣ x ∗ − x k + 1 ∣ = 0 \displaystyle \lim_{k \to \infty}|x^*-x_{k+1}|=0 k → ∞ lim ∣ x ∗ − x k + 1 ∣ = 0 x ∗ = x k + 1 ( k → ∞ ) x^*=x_{k+1}(k\to\infty) x ∗ = x k + 1 ( k → ∞ )
3:迭代法的误差式:
设某一次迭代后误差为ϵ \epsilon ϵ
∣ x k + 1 − x k ∣ = ∣ ( x ∗ − x k ) − ( x ∗ − x k + 1 ) ≥ ∣ x ∗ − x k ∣ − ∣ x ∗ − x k + 1 ∣ ≥ ∣ x ∗ − x k ∣ − L ∣ x ∗ − x k ∣ |x_{k+1}-x_{k}| = |(x^*-x_k)-(x^*-x_{k+1})\geq|x^*-x_k|-|x^*-x_{k+1}|\geq|x^*-x_k|-L|x^*-x_k| ∣ x k + 1 − x k ∣ = ∣ ( x ∗ − x k ) − ( x ∗ − x k + 1 ) ≥ ∣ x ∗ − x k ∣ − ∣ x ∗ − x k + 1 ∣ ≥ ∣ x ∗ − x k ∣ − L ∣ x ∗ − x k ∣
其中从∣ x ∗ − x k + 1 ∣ ≤ L ∣ x ∗ − x k ∣ |x^*-x_{k+1}| \leq L|x^*-x_k| ∣ x ∗ − x k + 1 ∣ ≤ L ∣ x ∗ − x k ∣
故可以轻松的计算出误差估计式为:
∣ x ∗ − x k ∣ ≤ 1 1 − L ∣ x k + 1 − x k ∣ |x^*-x_k|\leq\frac{1}{1-L}|x_{k+1}-x_k| ∣ x ∗ − x k ∣ ≤ 1 − L 1 ∣ x k + 1 − x k ∣
通过中值定理,又可以推出:
∣ x k + 1 − x k ∣ = ∣ φ ′ ( ξ ) ( x k − x k − 1 ) ∣ |x_{k+1}-x_k| = |\varphi'(\xi)(x_k-x_{k-1})| ∣ x k + 1 − x k ∣ = ∣ φ ′ ( ξ ) ( x k − x k − 1 ) ∣
因为∣ φ ′ ( ξ ) ∣ ≤ L |\varphi'(\xi)|\leq L ∣ φ ′ ( ξ ) ∣ ≤ L
∣ x ∗ − x k ∣ ≤ L k 1 − L ∣ x 1 − x 0 ∣ |x^*-x_k|\leq\frac{L^k}{1-L}|x_1-x_0| ∣ x ∗ − x k ∣ ≤ 1 − L L k ∣ x 1 − x 0 ∣
其中L可以近似的看作是一个足够接近方程解的函数导数的值。
3.3.3不动点迭代法的收敛速度
首先我们先直接给出一个结论:在不动点迭代过程中,第i步迭代和第i+1步迭代的表达式分别为 e i , e i + 1 e_i,e_{i+1} e i , e i + 1 lim i → ∞ e i + 1 e i = S < 1 ≠ 0 \displaystyle \lim_{ i \to \infty}\frac{e_{i+1}}{e_i}=S<1\neq0 i → ∞ lim e i e i + 1 = S < 1 = 0
如何能证明我们的算法是一个线性收敛的函数呢?实际上非常简单。证明过程如下:
若 φ ( x ) 连续可微 , 不动点的一个足够近似的值为 x 0 , x i + 1 和 x i 是两次迭代的估计值 若\varphi(x)连续可微,不动点的一个足够近似的值为x_0,x_{i+1}和x_i是两次迭代的估计值 若 φ ( x ) 连续可微 , 不动点的一个足够近似的值为 x 0 , x i + 1 和 x i 是两次迭代的估计值 根据中值定理, ∃ r ∈ ( x i , r ) , φ ( x i ) − x 0 x i − x 0 = φ ′ ( r ) 根据中值定理,\exists r\in (x_i,r),\frac{\varphi(x_i)-x_0}{x_i-x_0}=\varphi'(r) 根据中值定理, ∃ r ∈ ( x i , r ) , x i − x 0 φ ( x i ) − x 0 = φ ′ ( r ) φ ( x i ) = x i + 1 , 故 x i + 1 − r = φ ′ ( r ) ( x i − r ) \varphi(x_i) = x_{i+1},故x_{i+1}-r = \varphi'(r)(x_i-r) φ ( x i ) = x i + 1 , 故 x i + 1 − r = φ ′ ( r ) ( x i − r ) e i + 1 = ∣ φ ′ ( r ) ∣ e i ,即 S = ∣ φ ′ ( r ) ∣ 为常数 e_{i+1}=\left|\varphi'(r)\right|e_i,即S=\left|\varphi'(r)\right|为常数 e i + 1 = ∣ φ ′ ( r ) ∣ e i ,即 S = ∣ φ ′ ( r ) ∣ 为常数 我们可以在这里举几个例子,例如我们希望求函数f ( x ) = x 3 + x − 1 = 0 f(x) = x^3+x-1=0 f ( x ) = x 3 + x − 1 = 0 φ ( x ) = 1 − x 3 \varphi(x) = 1-x^3 φ ( x ) = 1 − x 3 e i + 1 = − 3 r 2 e i e_{i+1}=-3r^2e_i e i + 1 = − 3 r 2 e i φ ( x ) = 1 − x \varphi(x) = \sqrt{1-x} φ ( x ) = 1 − x φ ( x ) = 1 + 3 x 3 1 + 3 x 2 \varphi(x) = \frac{1+3x^3}{1+3x^2} φ ( x ) = 1 + 3 x 2 1 + 3 x 3
//todo 图片
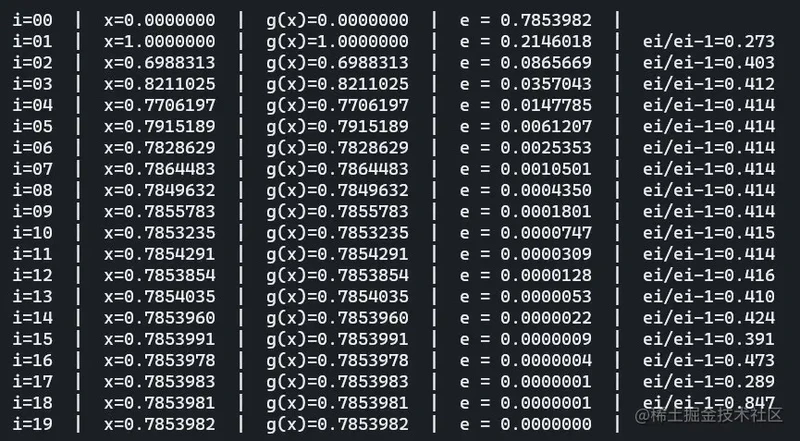
再举一个例子,函数f ( x ) = c o s x − s i n x = 0 f(x) = cosx-sinx=0 f ( x ) = cos x − s in x = 0 x = c o s x − s i n x + x = φ ( x ) x=cosx-sinx+x=\varphi(x) x = cos x − s in x + x = φ ( x )
不难看出我们的e i e i − 1 \frac{e_i}{e_{i-1}} e i − 1 e i S = ∣ φ ′ ( r ) ∣ = ∣ 1 − s i n r − c o s r ∣ ≈ 0.414 S=\left|\varphi'(r)\right|=|1-sinr-cosr|\approx0.414 S = ∣ φ ′ ( r ) ∣ = ∣1 − s in r − cosr ∣ ≈ 0.414
迭代的终止
3.4牛顿法
牛顿在整个微积分、数值分析中都有着举足轻重的地位,这里阐述的牛顿法,全名牛顿-拉夫逊法,就是Taylor展开式的一部分。牛顿迭代法的核心思想就是:设法将一个非线性方程f ( x ) = 0 f(x)=0 f ( x ) = 0 f ( x ) = 0 f(x)=0 f ( x ) = 0 x k x_k x k
p 1 ( x ) = f ( x k ) + f ′ ( x k ) ( x − x k ) p_1(x) = f(x_k)+f^{'}(x_k)(x-x_k) p 1 ( x ) = f ( x k ) + f ′ ( x k ) ( x − x k )
3.4.1普通牛顿法
从上述公式中我们知道,其中p 1 ( x ) p_1(x) p 1 ( x ) f ( x ) = 0 f(x)=0 f ( x ) = 0
x k + 1 = x k − f ( x k ) f ′ ( x k ) x_{k+1} = x_k - \frac{f(x_k)}{f^{'}(x_k)} x k + 1 = x k − f ′ ( x k ) f ( x k )
这就是普通牛顿法的迭代公式。在几何意义上,他就是一个切线与x轴的交点去逼近零点,如图:
我们不断的通过迭代这个过程,就能让我们的值越来越精确。
3.4.2牛顿下山法
所有的迭代法都有一个无法逃过的缺点,如果选取的初始值离根太远,则会导致迭代过程次数过多,并且有可能导致迭代发散,因为迭代法只具有局部收敛性。
为了避免迭代失败或时间过长,我们加上这样一个条件用于保证数值稳定下降
∣ f ( x k + 1 ) ∣ < ∣ f ( x k ) ∣ |f(x_{k+1})|<|f(x_k)| ∣ f ( x k + 1 ) ∣ < ∣ f ( x k ) ∣
将这个条件和牛顿法结合再一起,即再保证数值稳定下降的过程中,利用牛顿法加快迭代,这就是牛顿下山法。具体的操作如下:
将牛顿法的结果x ˉ k + 1 \bar{x}_{k+1} x ˉ k + 1 x k x_k x k x k + 1 x_{k+1} x k + 1
则有:
x k + 1 = λ x ˉ k + 1 + ( 1 − λ ) x k x_{k+1} = \lambda\bar{x}_{k+1} + (1-\lambda)x_k x k + 1 = λ x ˉ k + 1 + ( 1 − λ ) x k x k + 1 = x k − λ f ( x k ) f ′ ( x k ) x_{k+1} = x_k - \lambda\frac{f(x_k)}{f^{'}(x_k)} x k + 1 = x k − λ f ′ ( x k ) f ( x k )
其中λ ( 0 ≤ λ < 1 ) \lambda(0\leq\lambda<1) λ ( 0 ≤ λ < 1 ) ∣ f ( x k + 1 ) ∣ < ∣ f ( x k ) ∣ |f(x_{k+1})|<|f(x_k)| ∣ f ( x k + 1 ) ∣ < ∣ f ( x k ) ∣ x 0 x_0 x 0
3.4.3简单牛顿法
牛顿法可以说是一个非常有效的计算方法,准确度和迭代次数上都要比普通的迭代法要好得多,但是牛顿法最大的问题是我们需要求方程的导数,对于某些极其复杂的函数而言,导数是无法通过人工的方式计算,假如我们使用微积分的方式去求解导数,这对整个程序的性能会有比较大的影响,因此我们可以利用一个常数值λ \lambda λ
x k + 1 = x k − f ( x k ) λ x_{k+1} =x_k - \frac{f(x_k)}{\lambda} x k + 1 = x k − λ f ( x k )
不过对于常数λ \lambda λ x ∗ x^* x ∗
φ ( x ) = x − f ( x ) λ ⟹ φ ′ ( x ) = 1 − f ′ ( x ) λ \varphi(x) = x - \frac{f(x)}{\lambda}\Longrightarrow\varphi^{'}(x) = 1-\frac{f^{'}(x)}{\lambda} φ ( x ) = x − λ f ( x ) ⟹ φ ′ ( x ) = 1 − λ f ′ ( x )
牛顿迭代法的收敛性遵循前文中普通迭代法的收敛性,于是可以得到:
∣ φ ′ ( x ) ∣ = ∣ 1 − f ′ ( x ) λ ∣ ⟹ 0 < f ′ ( x ) c < 2 |\varphi^{'}(x)| = |1-\frac{f^{'}(x)}{\lambda}|\Longrightarrow0<\frac{f^{'}(x)}{c}<2 ∣ φ ′ ( x ) ∣ = ∣1 − λ f ′ ( x ) ∣ ⟹ 0 < c f ′ ( x ) < 2
这样我们就可以很轻松的确定下c的值了。
简单牛顿法的几何意义就简单许多了,和我们之前讨论的普通迭代法一致,只不过普通迭代法是将函数值和y = x y=x y = x y = λ ( x − x k ) + f ( x k ) y= \lambda(x-x_k)+f(x_k) y = λ ( x − x k ) + f ( x k )
public static double Newtown (Func<double , double > fx, Func<double , double > f1x, double x )var temp = f1x.Invoke(x);
if (temp == 0 )
{
throw new ArgumentException();
}
x = x - fx.Invoke(x) / temp;
if (Math.Abs(fx.Invoke(x)) <= epsilon)
{
return x;
}
return Newtown(fx, f1x, x);
}
3.4.4 改进牛顿法——弦截法
弦截法是牛顿法的一种改进,保留了牛顿法中收敛速度快的优点,还克服了再牛顿法中需要计算函数导数值f ′ f^{'} f ′
弦截法中,我们用差商
f ( x k ) − f ( x k − 1 ) x k − x k − 1 \frac{f(x_k)-f(x_{k-1})}{x_k-x_{k-1}} x k − x k − 1 f ( x k ) − f ( x k − 1 )
去代替牛顿法中的导数值,于是可以得到以下离散化的迭代
x k + 1 = x k − f ( x k ) f ( x k ) − f ( x k − 1 ) ( x k − x k − 1 ) x_{k+1} = x_k - \frac{f(x_k)}{f(x_k)-f(x_{k-1})}(x_k-x_{k-1}) x k + 1 = x k − f ( x k ) − f ( x k − 1 ) f ( x k ) ( x k − x k − 1 )
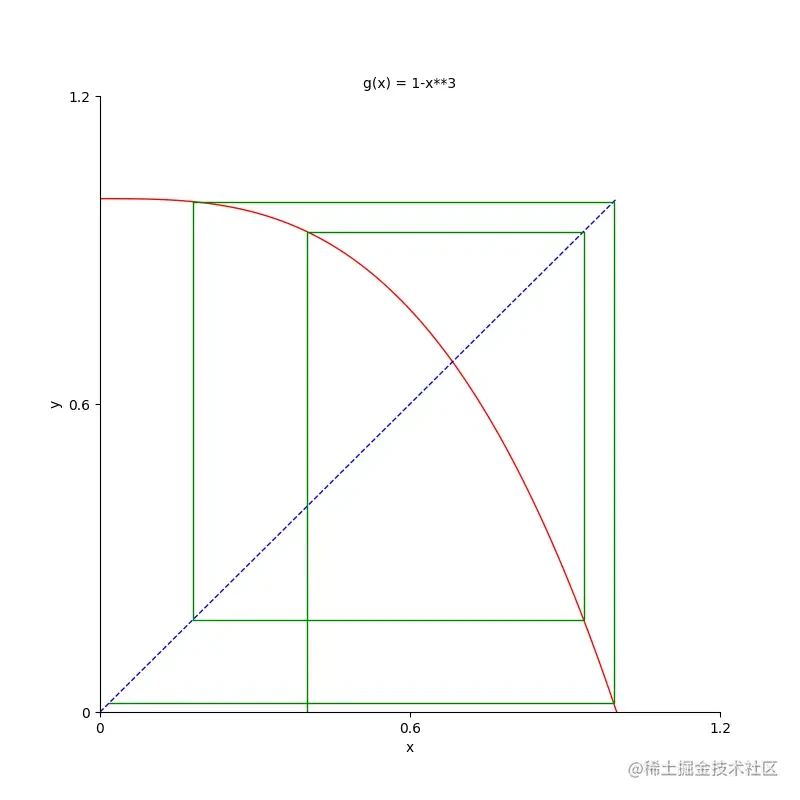
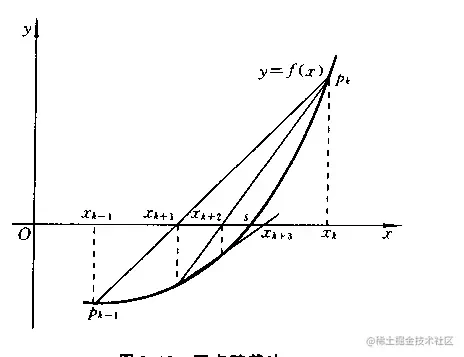
这种方法叫做双点弦截法,如图所示:
从图中可以知道,弦截法一直利用两点之间的连线作为迭代的内容,那么,他的合理性在哪里呢?
整个迭代法都离不开中值定理,这里也是这样,事实上,这个差商之所以可以对导数值进行替代,是因为中值定理中说过,连续函数中两函数上的点的连线的斜率必为两点之间某一点的导数值,并且迭代过程中,这两点的中值会越来越逼近函数零点,事实上这已经说明了弦截法是牛顿法的改进方法了。
不过,如果将函数中x k − 1 x_{k-1} x k − 1 x 0 x_0 x 0
public static double StringCut (Func<double , double > func, double x1, double x2 )var temp = x1 - (func.Invoke(x1) / (func.Invoke(x1) - func.Invoke(x2))) * (x1 - x2);
x2 = x1;
x1 = temp;
if (Math.Abs(func.Invoke(x1)) <= epsilon)
{
return x1;
}
return StringCut(func, x1, x2);
}
3.4.5 牛顿法的收敛性
牛顿法的收敛性有可能是一阶收敛也有可能是二阶收敛,具体要看我们的迭代函数。我们首先讲讲牛顿法二次收敛的情形。
假定我们牛顿法的迭代函数为g ( x ) = x − f ( x ) f ′ ( x ) g(x) = x-\frac{f(x)}{f'(x)} g ( x ) = x − f ′ ( x ) f ( x ) g ′ ( x ) = f ( x ) f ′ ′ ( x ) f ′ ( x ) 2 g'(x) = \frac{f(x)f''(x)}{f'(x)^2} g ′ ( x ) = f ′ ( x ) 2 f ( x ) f ′′ ( x ) g ′ ( r ) = 0 g'(r)=0 g ′ ( r ) = 0
我们再将f ( r ) f(r) f ( r ) x i x_i x i f ( r ) = 0 f(r)=0 f ( r ) = 0
f ( r ) = f ( x i ) + ( r − x i ) f ′ ( x i ) + ( r − x i ) 2 2 f ′ ′ ( ξ ) , ξ ∈ ( x i , r ) f(r) = f(x_i)+(r-x_i)f'(x_i)+\frac{(r-x_i)^2}{2}f''(\xi),\xi \in (x_i,r) f ( r ) = f ( x i ) + ( r − x i ) f ′ ( x i ) + 2 ( r − x i ) 2 f ′′ ( ξ ) , ξ ∈ ( x i , r ) f ( r ) = 0 = > x i − f ( x i ) f ′ ( x i ) − r = ( r − x i ) 2 2 f ′ ′ ( ξ ) f ′ ( x i ) f(r) = 0 =>x_i-\frac{f(x_i)}{f'(x_i)} -r = \frac{(r-x_i)^2}{2}\frac{f''(\xi)}{f'(x_i)} f ( r ) = 0 => x i − f ′ ( x i ) f ( x i ) − r = 2 ( r − x i ) 2 f ′ ( x i ) f ′′ ( ξ ) 若f ′ ( x i ) ≠ 0 f'(x_i)\neq0 f ′ ( x i ) = 0
x i + 1 − r = e i 2 f ′ ′ ( ξ ) 2 f ′ ( x i ) x_{i+1}-r=e_i^2\frac{f''(\xi)}{2f'(x_i)} x i + 1 − r = e i 2 2 f ′ ( x i ) f ′′ ( ξ )
e i + 1 = e i 2 ∣ f ′ ′ ( ξ ) 2 f ′ ( x i ) ∣ e_{i+1} = e_i^2\left|\frac{f''(\xi)}{2f'(x_i)}\right| e i + 1 = e i 2 ∣ ∣ 2 f ′ ( x i ) f ′′ ( ξ ) ∣ ∣
这样我们就得到了牛顿法的二阶收敛的定义,对于二阶收敛,我们要求是需要在该处的一阶导数值不为0。
不过我们的牛顿法并不是总为二次收敛的,在面临多重根的时候,牛顿法往往会倒退到线性收敛的速度。,例如函数f ( x ) = x m f(x)=x^m f ( x ) = x m
x i + 1 = x i − x i m m x i m − 1 = m − 1 m x i x_{i+1} = x_i-\frac{x_i^m}{mx_i^{m-1}}=\frac{m-1}{m}x_i x i + 1 = x i − m x i m − 1 x i m = m m − 1 x i 唯一的根是0,但是0是一个m-1重根,因此得到
e i + 1 = S e i , S = m − 1 m e_{i+1} = Se_i,S=\frac{m-1}{m} e i + 1 = S e i , S = m m − 1 我们这里可以给出一个定义,若m+1阶连续可微函数有一个m重根,那么利用牛顿法会线性局部收敛,误差式如上。
收敛迭代的加速与精度
利用迭代法进行收敛的计算时,往往面临一个很麻烦的问题,就是当运行足够多次迭代的时候,我们的精度往往会不降反升,这是因为一种类似摇摆的问题出现,例如我规定此刻你站在坐标1上,我希望你走到坐标0上,你每次可以向左或者向右走三步,那么第一次你向左走三步之后,得到的迭代结果时-2,反而离精确值更远了。这是一个令人糟心的问题。这里我们对这种现象进行一次解释。
收敛的精度
y还是x?
事实上我们的误差分为了前向误差和后向误差,什么是前向误差呢?实际上就是我们要求解的根与实际的差值,假设f ( r ) = 0 f(r)=0 f ( r ) = 0 ∣ r − x i ∣ \left|r-x_i\right| ∣ r − x i ∣ \left|f(x_i)|
对于计算机而言,存储的精度是有极限的,假定我们现在有一台古老的计算机,他的存储精度最多就到小数点后4位,那么假设我们的迭代函数是f ( x ) = x 2 f(x)=x^2 f ( x ) = x 2 f ( 0.001 ) = 0.000001 f(0.001)=0.000001 f ( 0.001 ) = 0.000001
这其实就是我们后向误差足够小,但是前向误差并不够小导致的。我们在实际的代码编写的时候,一定要注意的一个地方就是我们的误差在什么时候应当利用前向误差进行终止,什么时候又应该利用后向误差进行求解。
敏感性
读者可以尝试将迭代初始值设置成我们方程实际的根进行迭代,按着我们正常人的理解,他应该立即停止迭代直接返回我们的初始值即可。但是算法往往是不尽人意的,在绝大多数工具或语言的内置求根函数中,即使我们传入的初始值是根,往往得到的结果反而是一个不精确的解。例如著名的威尔金森多项式:
W ( x ) = ( x − 1 ) ( x − 2 ) . . . ( x − 20 ) W(x) = (x-1)(x-2)...(x-20) W ( x ) = ( x − 1 ) ( x − 2 ) ... ( x − 20 ) 如果我们利用这个已经因式分解好了的式子进行求根运算,这似乎没有必要,我们可以得到一个非常工整的方程根,他就是1-20之间所有的自然数组成,一旦我们将其展开后投入运算,由于存在许多大数字,很多大数字会因为存储、计算等过程中产生损失和误差,这些误差实际上是很小的数字,但是却对我们的计算结果产生了很大的误差,最终我们难以得到一个精确解。这就是对于求根过程中对数字扰动的敏感性问题。
我们进一步去探索一下究竟是什么导致了误差放大,并且能粗略的计算出这些误差究竟有多少,我们假设是寻找一个函数f ( x ) = 0 f(x)=0 f ( x ) = 0 ϵ g ( x ) \epsilon g(x) ϵ g ( x ) ϵ \epsilon ϵ Δ r \Delta r Δ r
f ( r + Δ r ) + ϵ g ( r + Δ r ) = 0 f(r+\Delta r)+\epsilon g(r+\Delta r) = 0 f ( r + Δ r ) + ϵ g ( r + Δ r ) = 0 将上式统统泰勒展开
f ( r ) + ( Δ r ) f ′ ( r ) + ϵ g ( r ) + ϵ ( Δ r ) g ′ ( r ) + O ( ( Δ r ) 2 ) = 0 , 其中 O ( ( Δ r ) 2 ) → 0 , Δ r → 0 f(r)+(\Delta r)f'(r)+\epsilon g(r)+\epsilon(\Delta r)g'(r)+O((\Delta r)^2) = 0,其中\displaystyle O((\Delta r)^2) \to 0,\Delta r \to 0 f ( r ) + ( Δ r ) f ′ ( r ) + ϵ g ( r ) + ϵ ( Δ r ) g ′ ( r ) + O (( Δ r ) 2 ) = 0 , 其中 O (( Δ r ) 2 ) → 0 , Δ r → 0 忽略后面的高阶无穷小,同时r又是根,于是可以得到一个关于r的变化值的近似
Δ r ( f ′ ( r ) + ϵ g ′ ( r ) ) ≈ − f ( r ) − ϵ g ( r ) = − ϵ g ( r ) \Delta r (f'(r)+\epsilon g'(r)) \approx -f(r)-\epsilon g(r) =-\epsilon g(r) Δ r ( f ′ ( r ) + ϵ g ′ ( r )) ≈ − f ( r ) − ϵ g ( r ) = − ϵ g ( r ) 又因为ϵ \epsilon ϵ f ′ ( r ) f'(r) f ′ ( r ) Δ r \Delta r Δ r
Δ r ≈ − ϵ g ( r ) f ′ ( r ) \Delta r \approx -\epsilon\frac{g(r)}{f'(r)} Δ r ≈ − ϵ f ′ ( r ) g ( r ) 这就是我们根的敏感性公式,利用这个公式,我们可以得出,如果出现了某些数字的扰动,根会如何变化。
这里举一个黄皮书上的例子,如果函数P ( x ) = ( x − 1 ) ( x − 2 ) . . . ( x − 6 ) − 1 0 − 6 x 7 P(x) = (x-1)(x-2)...(x-6)-10^{-6}x^7 P ( x ) = ( x − 1 ) ( x − 2 ) ... ( x − 6 ) − 1 0 − 6 x 7
那么我们直接设近似函数为f ( x ) = ( x − 1 ) ( x − 2 ) . . . ( x − 6 ) f(x)=(x-1)(x-2)...(x-6) f ( x ) = ( x − 1 ) ( x − 2 ) ... ( x − 6 ) ϵ g ( x ) = − 1 0 − 6 x 7 \epsilon g(x)=-10^{-6}x^7 ϵ g ( x ) = − 1 0 − 6 x 7
Δ r ≈ − ϵ g ( r ) f ′ ( r ) = 2332.8 × 1 0 − 6 \Delta r \approx -\epsilon\frac{g(r)}{f'(r)} = 2332.8\times 10^{-6} Δ r ≈ − ϵ f ′ ( r ) g ( r ) = 2332.8 × 1 0 − 6 因此我们估计的最大根应当是6.0023328左右,读者可以自行使用迭代法去求解最大根,最后得出的结果与这个估计值是极度接近的。这里我们定义一个新东西误差放大因子 ,也就是我们的∣ g ( r ) r f ′ ( r ) ∣ \left|\frac{g(r)}{rf'(r)}\right| ∣ ∣ r f ′ ( r ) g ( r ) ∣ ∣
普通迭代加速
对于迭代过程,利用中值定理有
x ∗ − x k + 1 = φ ( x ∗ ) − φ ( x k ) = φ ′ ( ξ ) ( x ∗ − x k ) x^*-x_{k+1} = \varphi(x^*)-\varphi(x_k) = \varphi^{'}(\xi)(x^*-x_k) x ∗ − x k + 1 = φ ( x ∗ ) − φ ( x k ) = φ ′ ( ξ ) ( x ∗ − x k )
当Δ x → 0 \Delta x \rightarrow0 Δ x → 0 φ ′ ( ξ ) \varphi^{'}(\xi) φ ′ ( ξ ) λ ( λ < 1 ) \lambda(\lambda<1) λ ( λ < 1 )
于是有
λ ( x ∗ − x k ) = x ∗ − x k + 1 ⟶ x ∗ = 1 1 − λ x ˉ k + 1 − λ 1 − λ x k \lambda(x^*-x_k) = x^*-x_{k+1}\longrightarrow x^* = \frac{1}{1-\lambda}\bar{x}_{k+1}-\frac{\lambda}{1-\lambda}x_k λ ( x ∗ − x k ) = x ∗ − x k + 1 ⟶ x ∗ = 1 − λ 1 x ˉ k + 1 − 1 − λ λ x k
故可以推出最终的迭代公式为
{ x ˉ k + 1 = φ ( x k ) x k + 1 = x ˉ k + 1 + λ 1 − λ ( x ˉ k + 1 − x k ) \begin{cases}
\bar{x}_{k+1} = \varphi(x_k)\\
x_{k+1} = \bar{x}_{k+1} + \frac{\lambda}{1-\lambda}(\bar{x}_{k+1}-x_k)
\end{cases} { x ˉ k + 1 = φ ( x k ) x k + 1 = x ˉ k + 1 + 1 − λ λ ( x ˉ k + 1 − x k ) 利用这种方式的好处就是再求得x k x_k x k x ˉ k + 1 < x k + 1 \bar{x}_{k+1}<x_{k+1} x ˉ k + 1 < x k + 1
Atiken加速法
Atiken加速法其实就是再普通加速迭代公式上在进行一次迭代,这里直接写出公式:
{ x ˉ k + 1 = φ ( x k ) x ˉ ˉ k + 1 = φ ( x ˉ k + 1 ) x k + 1 = x ˉ ˉ k + 1 − ( x ˉ ˉ k + 1 − x ˉ k + 1 ) x ˉ ˉ k + 1 − 2 x ˉ k + 1 + x k \begin{cases}
\bar{x}_{k+1} = \varphi(x_k)\\
\bar{\bar{x}}_{k+1} = \varphi(\bar{x}_{k+1})\\
x_{k+1} = \bar{\bar{x}}_{k+1} - \frac{(\bar{\bar{x}}_{k+1}-\bar{x}_{k+1})}{\bar{\bar{x}}_{k+1} - 2\bar{x}_{k+1}+x_k}
\end{cases} ⎩ ⎨ ⎧ x ˉ k + 1 = φ ( x k ) x ˉ ˉ k + 1 = φ ( x ˉ k + 1 ) x k + 1 = x ˉ ˉ k + 1 − x ˉ ˉ k + 1 − 2 x ˉ k + 1 + x k ( x ˉ ˉ k + 1 − x ˉ k + 1 ) 练习题
试着不借助计算器计算2 \sqrt{2} 2
试着证明f ( x ) = a x + b f(x)=ax+b f ( x ) = a x + b
编程题:由一个高度为10m的圆柱构成的发射井顶部是一个半球,体积400 m 3 400m^3 400 m 3
设函数为f ( x ) = x n − a x n − 1 , g ( x ) = x n f(x)=x^n-ax^{n-1},g(x)=x^n f ( x ) = x n − a x n − 1 , g ( x ) = x n f ϵ ( x ) = x n − a x n − 1 + ϵ x n f_\epsilon(x) = x^n-ax^{n-1}+\epsilon x^n f ϵ ( x ) = x n − a x n − 1 + ϵ x n
Reference
《数值分析》(原书第二版) —— Timothy Sauer
《数值计算方法》(清华大学出版社) —— 吕同富等