一、级数法求解l阶勒让德方程
阶勒让德方程，即
%5Cfrac%7B%5Cmathrm%7Bd%7D%5E2%5CTheta%7D%7B%5Cmathrm%7Bd%7Dx%5E2%7D-2x%5Cfrac%7B%5Cmathrm%7Bd%7D%5CTheta%7D%7B%5Cmathrm%7Bd%7Dx%7D%2Bl(l%2B1)%5CTheta%3D0%0A%20%5Cend%7Bequation%7D%5Clabel%7Beq17%7D)
是
阶连带勒让德方程
%5Cfrac%7B%5Cmathrm%7Bd%7D%5E2%5CTheta%7D%7B%5Cmathrm%7Bd%7Dx%5E2%7D-2x%5Cfrac%7B%5Cmathrm%7Bd%7D%5CTheta%7D%7B%5Cmathrm%7Bd%7Dx%7D%2B%5Cleft%5Bl(l%2B1)-%5Cfrac%7Bm%5E2%7D%7B1-x%5E2%7D%5Cright%5D%5CTheta%3D0%5Clabel%7Beq16%7D%0A%20%5Cend%7Bequation%7D)
当
的特殊情况，它是一个线性二阶常微分方程，可以使用级数法求解。所谓级数解法，就是在某个任选定的点
的邻域上，把待求解表示成为有待定系数的级数，带入方程逐一确定系数。下面就用此方法求阶勒让德方程在
的邻域上的解。
首先将方程化为线性二阶常微分方程的标准形式：
%7D%7B1-x%5E2%7D%5CTheta%3D0%0A%20%5Cend%7Bequation%7D)
在处，%3D0)
，%3Dl(l%2B1))
，均为有限值，)
和)
在此处必然解析，所以
是方程的一个常点，所以方程具有泰勒展开的形式，即
%3Da_0%2Ba_1x%2Ba_2x%5E2%2B%5Ccdots%2Ba_k%20x%5Ek%2B%5Ccdots%0A%5Cend%7Bequation%7D)
于是有
%3Da_1%2B2a_2x%2B3a_3x%5E2%2B%5Ccdots%2B(k%2B1)a_%7Bk%2B1%7D%20x%5Ek%2B%5Ccdots%0A%5Cend%7Bequation*%7D%0A)
%3Da_2%2B6a_3x%2B12a_4x%5E2%2B%5Ccdots%2B(k%2B2)(k%2B1)a_%7Bk%2B2%7D%20x%5Ek%2B%5Ccdots%0A%5Cend%7Bequation*%7D)
把它们再带回勒让德方程中，合并同幂次项，有
![]()
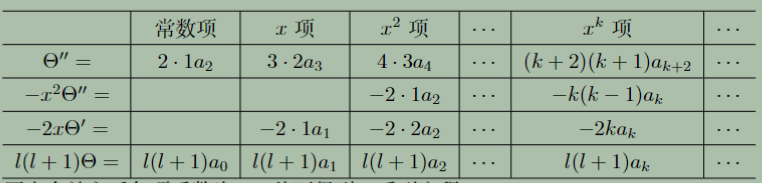
同幂次项的列表幂次合并之后各项系数为，从而得到一系列方程：
(k%2B1)a_%7Bk%2B2%7D%2B(l%5E2%2Bl-k%5E2-k)a_k%3D0%0A%20%5Cend%7Bequation%7D)
可以得到一般的递推公式为
(k%2B1)%7Da_k%0A%20%5Cend%7Bequation%7D)
按照递推公式进行具体的系数递推，可以得到
(2k-4-l)%5Ccdots%20(2-l)(-l)%5Ccdot(l%2B1)(l%2B3)%5Ccdots%20(l%2B2k-1)%7D%7B(2k)!%7Da_0%0A%5Cend%7Bequation%7D%0A)
(2k-3-l)%5Ccdots%20(1-l)%5Ccdot(l%2B2)(l%2B4)%5Ccdots%20(l%2B2k)%7D%7B(2k%2B1)!%7Da_1%0A%5Cend%7Bequation%7D)
这样我们就得到了阶勒让德方程的解：
%3Da_0%5CTheta_0(x)%2Ba_1%5CTheta_1(x)%3D%5Csum%5E%7B%5Cinfty%7D_%7Bn%3D0%7Da_%7B2n%7D%20x%5E%7B2n%7D%20%2B%5Csum%5E%7B%5Cinfty%7D_%7Bm%3D0%7Da_%7B2m%2B1%7D%20x%5E%7B2m%2B1%7D%20%20%0A%5Cend%7Bequation%7D)
我们还需要确认级数)
和)
的收敛半径，由递推公式知，二者的收敛半径为：
(n%2B1)%7D%7B(n-l)(n%2Bl%2B1)%7D%5Cright%7C%3D1%0A%5Cend%7Bequation%7D)
因此该级数的收敛半径为
，下面讨论级数在处是否收敛。
